Learning Outcomes
- Find the maximum of a quadratic function that models area, and revenue.
There are many real-world scenarios that involve finding the maximum or minimum value of a quadratic function, such as applications involving area and revenue. In this lesson, we will explore a way to maximize the area of a fenced enclosure, as well as how selling price can affect the number of units sold.
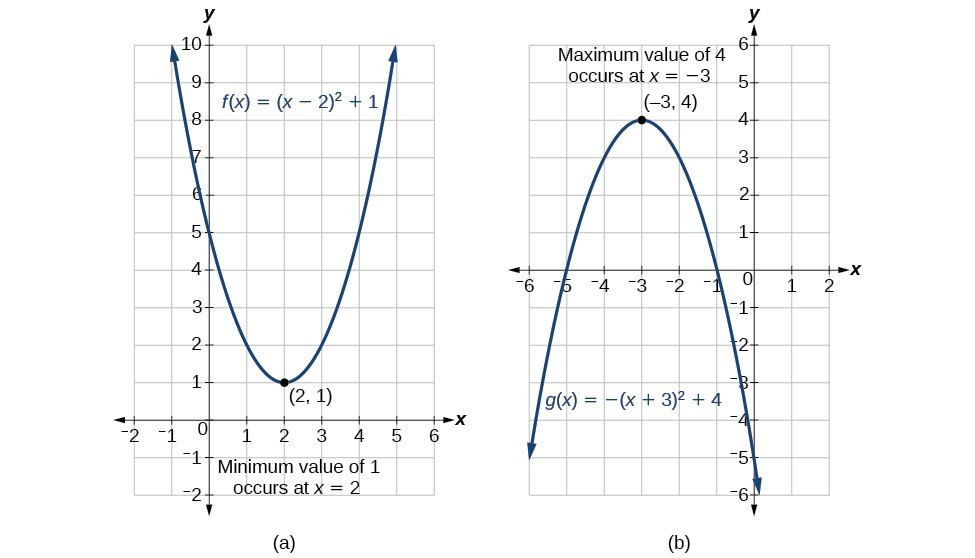
In graph (a) below, the parabola has a minimum value at [latex](2,1)[/latex], and the parabola in graph (b) has a maximum at [latex](-3,4)[/latex]. These values can take on meaning in applications such as the examples we will work through next.
Example: Finding the Maximum Value of a Quadratic Function
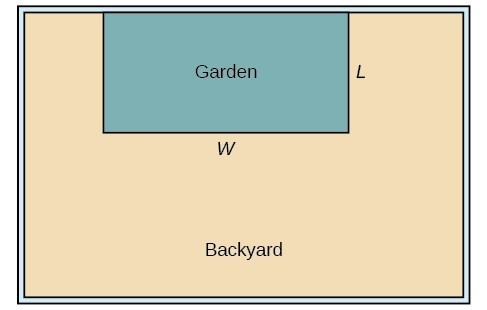
A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.
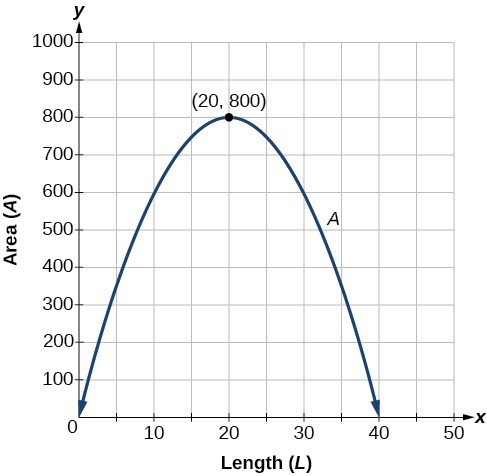
- Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length [latex]L[/latex].
- What dimensions should she make her garden to maximize the enclosed area?
The problem we solved above is called a constrained optimization problem. We can optimize our desired outcome given a constraint, which in this case was a limited amount of fencing materials. Try it yourself in the next problem.
Try It
How To: Given an application involving revenue, use a quadratic equation to find the maximum.
- Write a quadratic equation for revenue.
- Find the vertex of the quadratic equation.
- Determine the [latex]y[/latex]-value of the vertex.
Example: Finding Maximum Revenue
The unit price of an item affects its supply and demand. That is, if the unit price goes up, the demand for the item will usually decrease. For example, a local newspaper currently has 84,000 subscribers at a quarterly charge of $30. Market research has suggested that if the owners raise the price to $32, they would lose 5,000 subscribers. Assuming that subscriptions are linearly related to the price, what price should the newspaper charge for a quarterly subscription to maximize their revenue?
In the example above, we knew the number of subscribers to a newspaper and used that information to find the optimal price for each subscription. What if the price of subscriptions is affected by competition?
Try it
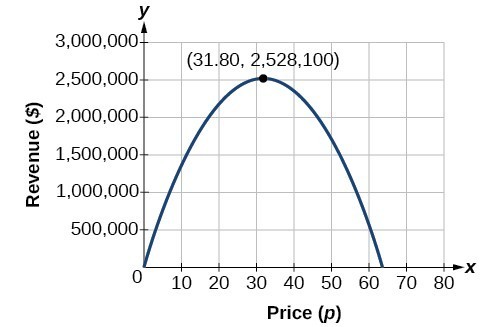
Previously, we found a quadratic function that modeled revenue as a function of price.
[latex]\text{Revenue}-2,500{p}^{2}+159,000p[/latex]
We found that selling the paper at [latex]\$31.80[/latex] per subscription would maximize revenue. What if your closest competitor sells their paper for [latex]\$25.00[/latex] per subscription? What is the maximum revenue you can make you sell your paper for the same?