Learning Outcomes
- Combine functions using algebraic operations.
- Create a new function by composition of functions.
Function composition, as we saw in the introduction and as we’ll explore in detail later in this section, is a way to combine existing functions. Another way to combine functions is to carry out the usual algebraic operations on functions, such as addition, subtraction, multiplication and division. We do this by performing the operations with the function outputs, defining the result as the output of our new function.
Suppose we need to add two columns of numbers that represent a husband and wife’s separate annual incomes over a period of years, with the result being their total household income. We want to do this for every year, adding only that year’s incomes and then collecting all the data in a new column. If [latex]w\left(y\right)[/latex] is the wife’s income and [latex]h\left(y\right)[/latex] is the husband’s income in year [latex]y[/latex], and we want [latex]T[/latex] to represent the total income, then we can define a new function.
If this holds true for every year, then we can focus on the relation between the functions without reference to a year and write
Just as for this sum of two functions, we can define difference, product, and ratio functions for any pair of functions that have the same kinds of inputs (not necessarily numbers) and also the same kinds of outputs (which do have to be numbers so that the usual operations of algebra can apply to them, and which also must have the same units or no units when we add and subtract). In this way, we can think of adding, subtracting, multiplying, and dividing functions.
For two functions [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)[/latex] with real number outputs, we define new functions [latex]f+g,f-g,f\cdot{g}[/latex], and [latex]\dfrac{f}{g}[/latex] by the relations
Example: Performing Algebraic Operations on Functions
Find and simplify the functions [latex]\left(g-f\right)\left(x\right)[/latex] and [latex]\left(\dfrac{g}{f}\right)\left(x\right)[/latex], given [latex]f\left(x\right)=x - 1[/latex] and [latex]g\left(x\right)={x}^{2}-1[/latex]. Give the domain of your result. Are they the same function?
recall operations on algebraic expressions
See Module 2: Polynomial and Rational Expressions for a refresher on how to do operations on algebraic expressions.
- Use order of operations when multiple operations are present
- When subtracting one polynomial expression from another, be sure to subtract each term of the second from the first
- Use the distributive property when multiplying two polynomial expressions
Try It now
Find and simplify the functions [latex]\left(f\cdot{g}\right)\left(x\right)[/latex] and [latex]\left(f-g\right)\left(x\right)[/latex].
Are they the same function?
Try It
Let’s explore what happens to the graphs of functions that are combined using algebraic operations. Use an online graphing calculator to graph the following functions:
- [latex]f(x) = x^2+3x-4[/latex]
- [latex]g(x) = \dfrac{1}{x-1}[/latex]
Now, enter [latex]h(x) = f(x)+g(x)[/latex] into the next line.
Evaluate [latex]h(1)[/latex], why do you think you get this result?
Create a New Function Using a Composition
Performing algebraic operations on functions combines them into a new function, but we can also create functions by composing functions. When we wanted to compute a heating cost from a day of the year in the introductory example, we created a new function that takes a day as input and yields a cost as output. The process of combining functions so that the output of one function becomes the input of another is known as a composition of functions. The resulting function is known as a composite function. We represent this combination by the following notation:
[latex]\left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)[/latex]
We read the left-hand side as [latex]"f[/latex] composed with [latex]g[/latex] at [latex]x,"[/latex] and the right-hand side as [latex]"f[/latex] of [latex]g[/latex] of [latex]x."[/latex] The two sides of the equation have the same mathematical meaning and are equal. The open circle symbol [latex]\circ[/latex] is called the composition operator. We use this operator mainly when we wish to emphasize the relationship between the functions themselves without referring to any particular input value. Composition is a binary operation that takes two functions and forms a new function, much as addition or multiplication takes two numbers and gives a new number. However, it is important not to confuse function composition with multiplication because, as we learned above, in most cases [latex]f\left(g\left(x\right)\right)\ne f\left(x\right)g\left(x\right)[/latex].
It is also important to understand the order of operations in evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first, and then working to the outside. In the equation above, the function [latex]g[/latex] takes the input [latex]x[/latex] first and yields an output [latex]g\left(x\right)[/latex]. Then the function [latex]f[/latex] takes [latex]g\left(x\right)[/latex] as an input and yields an output [latex]f\left(g\left(x\right)\right)[/latex].
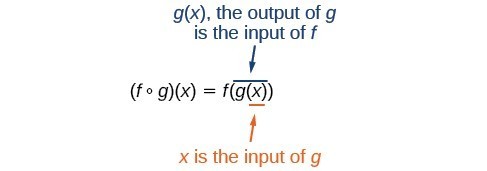
Figure 2
In general [latex]f\circ g[/latex] and [latex]g\circ f[/latex] are different functions. In other words in many cases [latex]f\left(g\left(x\right)\right)\ne g\left(f\left(x\right)\right)[/latex] for all [latex]x[/latex].
For example if [latex]f\left(x\right)={x}^{2}[/latex] and [latex]g\left(x\right)=x+2[/latex], then
[latex]\begin{align}f\left(g\left(x\right)\right)&=f\left(x+2\right) \\[2mm] &={\left(x+2\right)}^{2} \\[2mm] &={x}^{2}+4x+4\hfill \end{align}[/latex]
but
[latex]\begin{align}g\left(f\left(x\right)\right)&=g\left({x}^{2}\right) \\[2mm] \text{ }&={x}^{2}+2\hfill \end{align}[/latex]
These expressions are not equal for all values of [latex]x[/latex], so the two functions are not equal. It is irrelevant that the expressions happen to be equal for the single input value [latex]x=-\frac{1}{2}[/latex].
Note that the range of the inside function (the first function to be evaluated) needs to be within the domain of the outside function. Less formally, the composition has to make sense in terms of inputs and outputs. Additionally, in applied settings, function composition usually only makes sense in one specific order.
A General Note: Composition of Functions
When the output of one function is used as the input of another, we call the entire operation a composition of functions. For any input [latex]x[/latex] and functions [latex]f[/latex] and [latex]g[/latex], this action defines a composite function, which we write as [latex]f\circ g[/latex] such that
[latex]\left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)[/latex]
The domain of the composite function [latex]f\circ g[/latex] is all [latex]x[/latex] such that [latex]x[/latex] is in the domain of [latex]g[/latex] and [latex]g\left(x\right)[/latex] is in the domain of [latex]f[/latex].
It is important to realize that the product of functions [latex]fg[/latex] is not the same as the function composition [latex]f\left(g\left(x\right)\right)[/latex], because, in general, [latex]f\left(x\right)g\left(x\right)\ne f\left(g\left(x\right)\right)[/latex].
Example: Define a Composition of Functions
Using the functions provided, find [latex]f\left(g\left(x\right)\right)[/latex] and [latex]g\left(f\left(x\right)\right)[/latex].
[latex]f\left(x\right)=2x+1\\g\left(x\right)=3-x[/latex]
try it now
Now we will explore the graph of a composition of functions. Use an online graphing calculator to graph the following functions:
- [latex]f(x) = x^2+3x-4[/latex]
- [latex]g(x) = \dfrac{1}{x-1}[/latex]
Now define a new function:
[latex]h(x) = f(f(x))[/latex]
Now zoom in (use the plus sign in the upper right-hand corner of the graph) on the point [latex](0.23607,-3.236)[/latex], notice that both graphs pass through this point. Continue this pattern for a few more iterations: define a new function that contains another composition of [latex]f(x)[/latex] with itself. For example: [latex]p(x) = f(f(f(x)))[/latex], and so on. Continue to use the zoom as you iterate.
The point [latex](0.23607,-3.236)[/latex] is called a fixed point of the function [latex]f(x)=x^2+3x-4[/latex]. Fixed points are used in mathematical applications such as the page rank algorithm that Google uses to generate internet search results. Read more about fixed points here, and page rank here.
Example: Interpreting Composite Functions
The function [latex]c\left(s\right)[/latex] gives the number of calories burned completing [latex]s[/latex] sit-ups, and [latex]s\left(t\right)[/latex] gives the number of sit-ups a person can complete in [latex]t[/latex] minutes. Interpret [latex]c\left(s\left(3\right)\right)[/latex].
Example: Investigating the Order of Function Composition
Suppose [latex]f\left(x\right)[/latex] gives miles that can be driven in [latex]x[/latex] hours and [latex]g\left(y\right)[/latex] gives the gallons of gas used in driving [latex]y[/latex] miles. Which of these expressions is meaningful: [latex]f\left(g\left(y\right)\right)[/latex] or [latex]g\left(f\left(x\right)\right)?[/latex]
Try It
Q & A
Are there any situations where [latex]f\left(g\left(y\right)\right)[/latex] and [latex]g\left(f\left(x\right)\right)[/latex] would both be meaningful or useful expressions?
Yes. For many pure mathematical functions, both compositions make sense, even though they usually produce different new functions. In real-world problems, functions whose inputs and outputs have the same units also may give compositions that are meaningful in either order.
Try It
The gravitational force on a planet a distance [latex]r[/latex] from the sun is given by the function [latex]G\left(r\right)[/latex]. The acceleration of a planet subjected to any force [latex]F[/latex] is given by the function [latex]a\left(F\right)[/latex]. Form a meaningful composition of these two functions, and explain what it means.
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Question ID 111999. Authored by: Lumen Learning. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
- Question ID 32907. Authored by: Smart, Jim. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 5727. Authored by: Pepe,Mike. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 3674. Authored by: Rasmussen,Melonie, mb Lippman,David. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
