Learning Outcomes
- Find and evaluate the inverse of a function in tabular form.
- Find and evaluate the inverse of a function given as an equation.
- Graph a function and its inverse.
Once we have a one-to-one function, we can evaluate its inverse at specific inverse function inputs or construct a complete representation of the inverse function in many cases.
Inverting Tabular Functions
Suppose we want to find the inverse of a function represented in table form. Remember that the domain of a function is the range of the inverse and the range of the function is the domain of the inverse. So we need to interchange the domain and range.
Each row (or column) of inputs becomes the row (or column) of outputs for the inverse function. Similarly, each row (or column) of outputs becomes the row (or column) of inputs for the inverse function.
recall reading functions from tables
Look to see which row or column of a table is labeled as the input and which is labeled as the output.
The tables below indicate one row represents “[latex]t[/latex]” and the other, [latex]f(t)[/latex].
It is common for input to be represented by time when output is a distance.
Example: Interpreting the Inverse of a Tabular Function
A function [latex]f\left(t\right)[/latex] is given below, showing distance in miles that a car has traveled in [latex]t[/latex] minutes. Find and interpret [latex]{f}^{-1}\left(70\right)[/latex].
| [latex]t\text{ (minutes)}[/latex] | 30 | 50 | 70 | 90 |
| [latex]f\left(t\right)\text{ (miles)}[/latex] | 20 | 40 | 60 | 70 |
Try It
Using the table below, find and interpret (a) [latex]\text{ }f\left(60\right)[/latex], and (b) [latex]\text{ }{f}^{-1}\left(60\right)[/latex].
| [latex]t\text{ (minutes)}[/latex] | 30 | 50 | 60 | 70 | 90 |
| [latex]f\left(t\right)\text{ (miles)}[/latex] | 20 | 40 | 50 | 60 | 70 |
Evaluating the Inverse of a Function, Given a Graph of the Original Function
The domain of a function can be read by observing the horizontal extent of its graph. We find the domain of the inverse function by observing the vertical extent of the graph of the original function, because this corresponds to the horizontal extent of the inverse function. Similarly, we find the range of the inverse function by observing the horizontal extent of the graph of the original function, as this is the vertical extent of the inverse function. If we want to evaluate an inverse function, we find its input within its domain, which is all or part of the vertical axis of the original function’s graph.
How To: Given the graph of a function, evaluate its inverse at specific points.
- Find the desired input of the inverse function on the [latex]y[/latex]-axis of the given graph.
- Read the inverse function’s output from the [latex]x[/latex]-axis of the given graph.
Example: Evaluating a Function and Its Inverse from a Graph at Specific Points
A function [latex]g\left(x\right)[/latex] is given below. Find [latex]g\left(3\right)[/latex] and [latex]{g}^{-1}\left(3\right)[/latex].

Try It
Using the graph in the previous example, (a) find [latex]{g}^{-1}\left(1\right)[/latex], and (b) estimate [latex]{g}^{-1}\left(4\right)[/latex].
Finding Inverses of Functions Represented by Formulas
Sometimes we will need to know an inverse function for all elements of its domain, not just a few. If the original function is given as a formula—for example, [latex]y[/latex] as a function of [latex]x-[/latex] we can often find the inverse function by solving to obtain [latex]x[/latex] as a function of [latex]y[/latex].
How To: Given a function represented by a formula, find the inverse.
- Verify that [latex]f[/latex] is a one-to-one function.
- Replace [latex]f\left(x\right)[/latex] with [latex]y[/latex].
- Interchange [latex]x[/latex] and [latex]y[/latex].
- Solve for [latex]y[/latex], and rename the function [latex]{f}^{-1}\left(x\right)[/latex].
Example: Inverting the Fahrenheit-to-Celsius Function
Find a formula for the inverse function that gives Fahrenheit temperature as a function of Celsius temperature.
[latex]C=\frac{5}{9}\left(F - 32\right)[/latex]
Try It
Solve for [latex]x[/latex] in terms of [latex]y[/latex] given [latex]y=\frac{1}{3}\left(x - 5\right)[/latex]
Example: Solving to Find an Inverse Function
Find the inverse of the function [latex]f\left(x\right)=\dfrac{2}{x - 3}+4[/latex].
Example: Solving to Find an Inverse with Radicals
Find the inverse of the function [latex]f\left(x\right)=2+\sqrt{x - 4}[/latex].
Try It
What is the inverse of the function [latex]f\left(x\right)=2-\sqrt{x}[/latex]? State the domains of both the function and the inverse function.
Use an online graphing calculator to graph the function, it’s inverse, and [latex]f(x) = x[/latex] to check whether you are correct.
Graph a Function’s Inverse
Now that we can find the inverse of a function, we will explore the graphs of functions and their inverses. Let us return to the quadratic function [latex]f\left(x\right)={x}^{2}[/latex] restricted to the domain [latex]\left[0,\infty \right)[/latex], on which this function is one-to-one, and graph it as below.
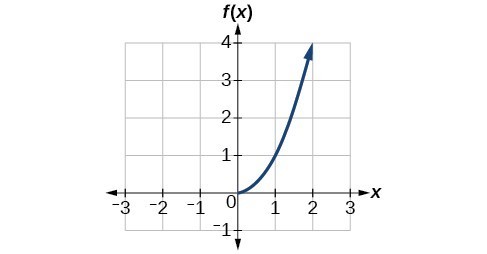
Quadratic function with domain restricted to [0, ∞).
Restricting the domain to [latex]\left[0,\infty \right)[/latex] makes the function one-to-one (it will obviously pass the horizontal line test), so it has an inverse on this restricted domain.
We already know that the inverse of the toolkit quadratic function is the square root function, that is, [latex]{f}^{-1}\left(x\right)=\sqrt{x}[/latex]. What happens if we graph both [latex]f\text{ }[/latex] and [latex]{f}^{-1}[/latex] on the same set of axes, using the [latex]x\text{-}[/latex] axis for the input to both [latex]f\text{ and }{f}^{-1}?[/latex]
We notice a distinct relationship: The graph of [latex]{f}^{-1}\left(x\right)[/latex] is the graph of [latex]f\left(x\right)[/latex] reflected about the diagonal line [latex]y=x[/latex], which we will call the identity line, shown below.
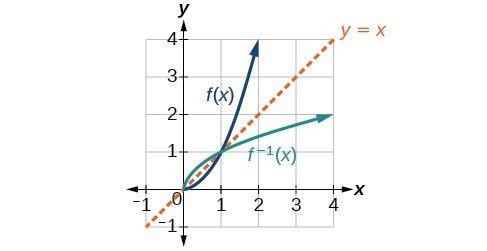
Square and square-root functions on the non-negative domain
This relationship will be observed for all one-to-one functions, because it is a result of the function and its inverse swapping inputs and outputs. This is equivalent to interchanging the roles of the vertical and horizontal axes.
Example: Finding the Inverse of a Function Using Reflection about the Identity Line
Given the graph of [latex]f\left(x\right)[/latex], sketch a graph of [latex]{f}^{-1}\left(x\right)[/latex].

Q & A
Is there any function that is equal to its own inverse?
Yes. If [latex]f={f}^{-1}[/latex], then [latex]f\left(f\left(x\right)\right)=x[/latex], and we can think of several functions that have this property. The identity function does, and so does the reciprocal function, because
[latex]\frac{1}{\frac{1}{x}}=x[/latex]
Any function [latex]f\left(x\right)=c-x[/latex], where [latex]c[/latex] is a constant, is also equal to its own inverse.


