Learning Outcomes
- Find the domain of a function defined by an equation.
- Write domain and range using standard notations.
In Functions and Function Notation, we were introduced to the concepts of domain and range. In this section we will practice determining domains and ranges for specific functions. Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples, such as tickets sales and year in the horror movie example above. We also need to consider what is mathematically permitted. For example, we cannot include any input value that leads us to take an even root of a negative number if the domain and range consist of real numbers. Or in a function expressed as a formula, we cannot include any input value in the domain that would lead us to divide by 0.
We can visualize the domain as a “holding area” that contains “raw materials” for a “function machine” and the range as another “holding area” for the machine’s products.
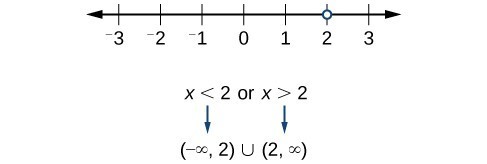
We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket [ when the set includes the endpoint and a parenthesis ( to indicate that the endpoint is either not included or the interval is unbounded. For example, if a person has $100 to spend, he or she would need to express the interval that is more than 0 and less than or equal to 100 and write [latex]\left(0,\text{ }100\right][/latex]. We will discuss interval notation in greater detail later.
Let’s turn our attention to finding the domain of a function whose equation is provided. Oftentimes, finding the domain of such functions involves remembering three different forms. First, if the function has no denominator or an even root, consider whether the domain could be all real numbers. Second, if there is a denominator in the function’s equation, exclude values in the domain that force the denominator to be zero. Third, if there is an even root, consider excluding values that would make the radicand negative.
Before we begin, let us review the conventions of interval notation:
- The smallest term from the interval is written first.
- The largest term in the interval is written second, following a comma.
- Parentheses, ( or ), are used to signify that an endpoint is not included, called exclusive.
- Brackets, [ or ], are used to indicate that an endpoint is included, called inclusive.
Example: Finding the Domain of a Function as a Set of Ordered Pairs
Find the domain of the following function: [latex]\left\{\left(2,\text{ }10\right),\left(3,\text{ }10\right),\left(4,\text{ }20\right),\left(5,\text{ }30\right),\left(6,\text{ }40\right)\right\}[/latex] .
Try It
Find the domain of the function:
[latex]\left\{\left(-5,4\right),\left(0,0\right),\left(5,-4\right),\left(10,-8\right),\left(15,-12\right)\right\}[/latex]
How To: Given a function written in equation form, find the domain.
- Identify the input values.
- Identify any restrictions on the input and exclude those values from the domain.
- Write the domain in interval form, if possible.
Example: Finding the Domain of a Function
Find the domain of the function [latex]f\left(x\right)={x}^{2}-1[/latex].
Try It
Find the domain of the function: [latex]f\left(x\right)=5-x+{x}^{3}[/latex].
How To: Given a function written in an equation form that includes a fraction, find the domain.
- Identify the input values.
- Identify any restrictions on the input. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for [latex]x[/latex] . These are the values that cannot be inputs in the function.
- Write the domain in interval form, making sure to exclude any restricted values from the domain.
Example: Finding the Domain of a Function Involving a Denominator (Rational Function)
Find the domain of the function [latex]f\left(x\right)=\dfrac{x+1}{2-x}[/latex].
Watch the following video to see more examples of how to find the domain of a rational function (one with a fraction).
Try It
Find the domain of the function: [latex]f\left(x\right)=\dfrac{1+4x}{2x - 1}[/latex].
How To: Given a function written in equation form including an even root, find the domain.
- Identify the input values.
- Since there is an even root, exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for [latex]x[/latex].
- The solution(s) are the domain of the function. If possible, write the answer in interval form.
division by zero and even roots of negative numbers
While zero divided by any number equals zero, division by zero results in an undefined ratio.
[latex]\dfrac{0}{a} = 0 \quad \text{but } \quad \dfrac{b}{0} = und[/latex]
An even root of a negative number does not exist in the real numbers.
[latex]\sqrt{-1} = i[/latex]
Since the domain of any function defined in the real plane is the set of all real input into the function, we must exclude any values of the input variable that create undefined expressions or even roots of a negative.
Example: Finding the Domain of a Function with an Even Root
Find the domain of the function [latex]f\left(x\right)=\sqrt{7-x}[/latex].
The next video gives more examples of how to define the domain of a function that contains an even root.
Try It
Find the domain of the function [latex]f\left(x\right)=\sqrt{5+2x}[/latex].
Q & A
Can there be functions in which the domain and range do not intersect at all?
Yes. For example, the function [latex]f\left(x\right)=-\frac{1}{\sqrt{x}}[/latex] has the set of all positive real numbers as its domain but the set of all negative real numbers as its range. As a more extreme example, a function’s inputs and outputs can be completely different categories (for example, names of weekdays as inputs and numbers as outputs, as on an attendance chart), in such cases the domain and range have no elements in common.
Try It
When you are defining the domain of a function, it can help to graph it, especially when you have a rational or a function with an even root.
First, determine the domain restrictions for the following functions, then graph each one to check whether your domain agrees with the graph.
- [latex]f(x) = \sqrt{2x-4}+5[/latex]
- [latex]g(x) = \dfrac{2x+4}{x-1}[/latex]
Next, use an online graphing calculator to evaluate your function at the domain restriction you found. What function value are you given?
How To: Given the formula for a function, determine the domain and range.
- Exclude from the domain any input values that result in division by zero.
- Exclude from the domain any input values that have nonreal (or undefined) number outputs.
- Use the valid input values to determine the range of the output values.
- Look at the function graph and table values to confirm the actual function behavior.
Example: Finding the Domain and Range Using Toolkit Functions
Find the domain and range of [latex]f\left(x\right)=2{x}^{3}-x[/latex].
Example: Finding the Domain and Range
Find the domain and range of [latex]f\left(x\right)=\dfrac{2}{x+1}[/latex].
Example: Finding the Domain and Range
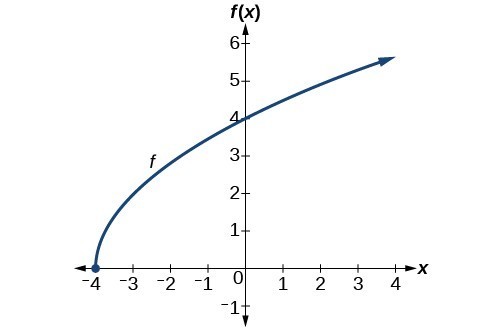
Find the domain and range of [latex]f\left(x\right)=2\sqrt{x+4}[/latex].
Try It
Find the domain and range of [latex]f\left(x\right)=-\sqrt{2-x}[/latex].