Learning Outcomes
- Identify the base of an exponential function and restrictions for its value.
- Evaluate exponential growth functions.
- Use the compound interest formula.
- Evaluate exponential functions with base e.
India is the second most populous country in the world with a population of about 1.25 billion people in 2013. The population is growing at a rate of about 1.2% each year.[1] If this rate continues, the population of India will exceed China’s population by the year 2031. When populations grow rapidly, we often say that the growth is “exponential.” To a mathematician, however, the term exponential growth has a very specific meaning. In this section, we will take a look at exponential functions, which model this kind of rapid growth.
The general form of the exponential formula is
[latex]f(x)=ab^x[/latex]
where [latex]a[/latex] is any nonzero number and [latex]b\neq1[/latex] is a positive real number.
- if [latex]b>1[/latex], the function grows at a rate proportional to its size.
- if [latex]0<b<1[/latex], the function decays at a rate proportional to its size.
The base of an exponential function must be a positive real number other than 1. Why do we limit the base b to positive values? This is done to ensure that the outputs will be real numbers. Observe what happens if the base is not positive:
- Consider a base of –9 and exponent of [latex]\frac{1}{2}[/latex]. Then [latex]f\left(x\right)=f\left(\frac{1}{2}\right)={\left(-9\right)}^{\frac{1}{2}}=\sqrt{-9}[/latex], which is not a real number.
Why do we limit the base to positive values other than 1? This is because a base of 1 results in the constant function. Observe what happens if the base is 1:
- Consider a base of 1. Then [latex]f\left(x\right)={1}^{x}=1[/latex] for any value of x.
To evaluate an exponential function with the form [latex]f\left(x\right)={b}^{x}[/latex], we simply substitute x with the given value, and calculate the resulting power. For example:
Let [latex]f\left(x\right)={2}^{x}[/latex]. What is [latex]f\left(3\right)[/latex]?
[latex]\begin{array}{llllllll}f\left(x\right)\hfill & ={2}^{x}\hfill & \hfill \\ f\left(3\right)\hfill & ={2}^{3}\text{}\hfill & \text{Substitute }x=3. \hfill \\ \hfill & =8\text{}\hfill & \text{Evaluate the power}\text{.}\hfill \end{array}[/latex]
When evaluating an exponential function, it is important to follow the order of operations. For example:
Let [latex]f\left(x\right)=30{\left(2\right)}^{x}[/latex]. What is [latex]f\left(3\right)[/latex]?
[latex]\begin{array}{c}f\left(x\right)\hfill & =30{\left(2\right)}^{x}\hfill & \hfill \\ f\left(3\right)\hfill & =30{\left(2\right)}^{3}\hfill & \text{Substitute }x=3.\hfill \\ \hfill & =30\left(8\right)\text{ }\hfill & \text{Simplify the power first}\text{.}\hfill \\ \hfill & =240\hfill & \text{Multiply}\text{.}\hfill \end{array}[/latex]
Note that if the order of operations were not followed, the result would be incorrect:
[latex]f\left(3\right)=30{\left(2\right)}^{3}\ne {60}^{3}=216,000[/latex]
Example: Evaluating Exponential Functions
Let [latex]f\left(x\right)=5{\left(3\right)}^{x+1}[/latex]. Evaluate [latex]f\left(2\right)[/latex] without using a calculator.
Try It
Let [latex]f\left(x\right)=8{\left(1.2\right)}^{x - 5}[/latex]. Evaluate [latex]f\left(3\right)[/latex] using a calculator. Round to four decimal places.
Because the output of exponential functions increases very rapidly, the term “exponential growth” is often used in everyday language to describe anything that grows or increases rapidly. However, exponential growth can be defined more precisely in a mathematical sense. If the growth rate is proportional to the amount present, the function models exponential growth.
A General Note: Exponential Growth
A function that models exponential growth grows by a rate proportional to the amount present. For any real number x and any positive real numbers a and b such that [latex]b\ne 1[/latex], an exponential growth function has the form
[latex]\text{ }f\left(x\right)=a{b}^{x}[/latex]
where
- a is the initial or starting value of the function.
- b is the growth factor or growth multiplier per unit x.
Tip for success
In mathematics, we carefully define terms, objects, and concepts so that there can be no ambiguity about what we mean. But such careful definition can be challenging to decipher. When reading definitions such as the one given above, it is helpful to write them out slowly by hand, perhaps more than once or twice, trying to explain each part to yourself as you go. That’s how you’ll build intuition for applying the term, object, or concept.
Be sure to read the surrounding text as well, such as the paragraph below. It will help you understand the definition in more general terms.
In more general terms, an exponential function consists of a constant base raised to a variable exponent. To differentiate between linear and exponential functions, let’s consider two companies, A and B. Company A has 100 stores and expands by opening 50 new stores a year, so its growth can be represented by the function [latex]A\left(x\right)=100+50x[/latex]. Company B has 100 stores and expands by increasing the number of stores by 50% each year, so its growth can be represented by the function [latex]B\left(x\right)=100{\left(1+0.5\right)}^{x}[/latex].
A few years of growth for these companies are illustrated below.
| Year, x | Stores, Company A | Stores, Company B |
|---|---|---|
| 0 | 100 + 50(0) = 100 | 100(1 + 0.5)0 = 100 |
| 1 | 100 + 50(1) = 150 | 100(1 + 0.5)1 = 150 |
| 2 | 100 + 50(2) = 200 | 100(1 + 0.5)2 = 225 |
| 3 | 100 + 50(3) = 250 | 100(1 + 0.5)3 = 337.5 |
| x | A(x) = 100 + 50x | B(x) = 100(1 + 0.5)x |
The graphs comparing the number of stores for each company over a five-year period are shown below. We can see that, with exponential growth, the number of stores increases much more rapidly than with linear growth.
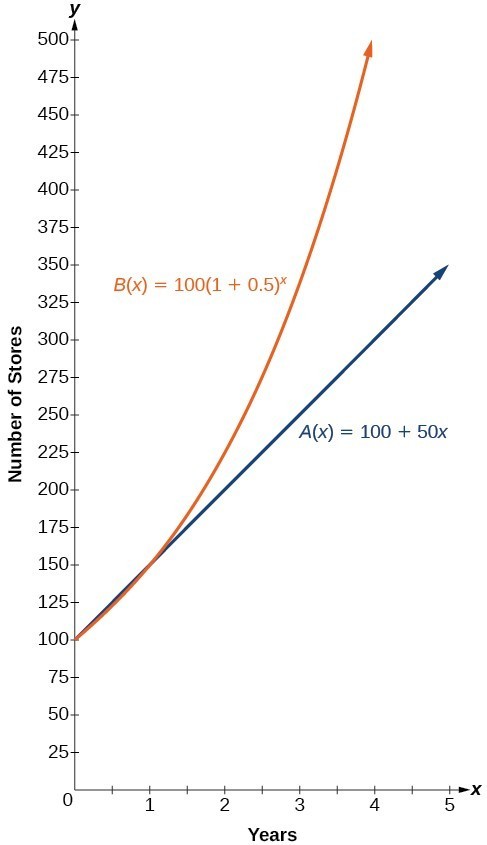
The graph shows the numbers of stores Companies A and B opened over a five-year period.
Notice that the domain for both functions is [latex]\left[0,\infty \right)[/latex], and the range for both functions is [latex]\left[100,\infty \right)[/latex]. After year 1, Company B always has more stores than Company A.
Let’s more closely examine the function representing the number of stores for Company B, [latex]B\left(x\right)=100{\left(1+0.5\right)}^{x}[/latex]. In this exponential function, 100 represents the initial number of stores, 0.5 represents the growth rate, and [latex]1+0.5=1.5[/latex] represents the growth factor. Generalizing further, we can write this function as [latex]B\left(x\right)=100{\left(1.5\right)}^{x}[/latex] where 100 is the initial value, 1.5 is called the base, and x is called the exponent.
Example: Evaluating a Real-World Exponential Model
At the beginning of this section, we learned that the population of India was about 1.25 billion in the year 2013 with an annual growth rate of about 1.2%. This situation is represented by the growth function [latex]P\left(t\right)=1.25{\left(1.012\right)}^{t}[/latex] where t is the number of years since 2013. To the nearest thousandth, what will the population of India be in 2031?
Try It
The population of China was about 1.39 billion in the year 2013 with an annual growth rate of about 0.6%. This situation is represented by the growth function [latex]P\left(t\right)=1.39{\left(1.006\right)}^{t}[/latex] where t is the number of years since 2013. To the nearest thousandth, what will the population of China be in the year 2031? How does this compare to the population prediction we made for India in the previous example?
Using the Compound Interest Formula
Savings instruments in which earnings are continually reinvested, such as mutual funds and retirement accounts, use compound interest. The term compounding refers to interest earned not only on the original value, but on the accumulated value of the account.
The annual percentage rate (APR) of an account, also called the nominal rate, is the yearly interest rate earned by an investment account. The term nominal is used when the compounding occurs a number of times other than once per year. In fact, when interest is compounded more than once a year, the effective interest rate ends up being greater than the nominal rate! This is a powerful tool for investing.
We can calculate compound interest using the compound interest formula which is an exponential function of the variables time t, principal P, APR r, and number of times compounded in a year n:
[latex]A\left(t\right)=P{\left(1+\frac{r}{n}\right)}^{nt}[/latex]
For example, observe the table below, which shows the result of investing $1,000 at 10% for one year. Notice how the value of the account increases as the compounding frequency increases.
| Frequency | Value after 1 year |
|---|---|
| Annually | $1100 |
| Semiannually | $1102.50 |
| Quarterly | $1103.81 |
| Monthly | $1104.71 |
| Daily | $1105.16 |
A General Note: The Compound Interest Formula
Compound interest can be calculated using the formula
[latex]A\left(t\right)=P{\left(1+\frac{r}{n}\right)}^{nt}[/latex]
where
- A(t) is the accumulated value of the account
- t is measured in years
- P is the starting amount of the account, often called the principal, or more generally present value
- r is the annual percentage rate (APR) expressed as a decimal
- n is the number of times compounded in a year
Example: Calculating Compound Interest
If we invest $3,000 in an investment account paying 3% interest compounded quarterly, how much will the account be worth in 10 years?
Tip for success
When calculating the value of an exponential function such as the compound interest formula, be careful when entering your calculation into a calculator. Use as many parentheses as needed to ensure your intent is clear. The calculator will apply order of operations as it is typed, which can cause an incorrect calculation for your equation.
Ex. To find the accumulated investment in the example above, you must calculate [latex]A\left(10\right)=3000\left(1+\frac{0.03}{4}\right)^{4\cdot 10}[/latex].
This would be entered in most scientific or graphing calculators as [latex]3000\left(1+(0.03/4)\right)\wedge\left(4\star10\right)[/latex].
Try It
An initial investment of $100,000 at 12% interest is compounded weekly (use 52 weeks in a year). What will the investment be worth in 30 years?
Example: Using the Compound Interest Formula to Solve for the Principal
A 529 Plan is a college-savings plan that allows relatives to invest money to pay for a child’s future college tuition; the account grows tax-free. Lily wants to set up a 529 account for her new granddaughter and wants the account to grow to $40,000 over 18 years. She believes the account will earn 6% compounded semi-annually (twice a year). To the nearest dollar, how much will Lily need to invest in the account now?
Try It
Refer to the previous example. To the nearest dollar, how much would Lily need to invest if the account is compounded quarterly?
Evaluating Exponential Functions with Base e
As we saw earlier, the amount earned on an account increases as the compounding frequency increases. The table below shows that the increase from annual to semi-annual compounding is larger than the increase from monthly to daily compounding. This might lead us to ask whether this pattern will continue.
Examine the value of $1 invested at 100% interest for 1 year compounded at various frequencies.
| Frequency | [latex]A\left(t\right)={\left(1+\frac{1}{n}\right)}^{n}[/latex] | Value |
|---|---|---|
| Annually | [latex]{\left(1+\frac{1}{1}\right)}^{1}[/latex] | $2 |
| Semiannually | [latex]{\left(1+\frac{1}{2}\right)}^{2}[/latex] | $2.25 |
| Quarterly | [latex]{\left(1+\frac{1}{4}\right)}^{4}[/latex] | $2.441406 |
| Monthly | [latex]{\left(1+\frac{1}{12}\right)}^{12}[/latex] | $2.613035 |
| Daily | [latex]{\left(1+\frac{1}{365}\right)}^{365}[/latex] | $2.714567 |
| Hourly | [latex]{\left(1+\frac{1}{\text{8766}}\right)}^{\text{8766}}[/latex] | $2.718127 |
| Once per minute | [latex]{\left(1+\frac{1}{\text{525960}}\right)}^{\text{525960}}[/latex] | $2.718279 |
| Once per second | [latex]{\left(1+\frac{1}{31557600}\right)}^{31557600}[/latex] | $2.718282 |
These values appear to be approaching a limit as n increases without bound. In fact, as n gets larger and larger, the expression [latex]{\left(1+\frac{1}{n}\right)}^{n}[/latex] approaches a number used so frequently in mathematics that it has its own name: the letter [latex]e[/latex]. This value is an irrational number, which means that its decimal expansion goes on forever without repeating. Its approximation to six decimal places is shown below.
understanding the number [latex]e[/latex]
The number [latex]e[/latex] is an irrational constant, like the number [latex]pi[/latex].
The number [latex]e[/latex] appears frequently in applications in the real world and is as important as numbers like [latex]0, 1, i, \text{ and } \pi[/latex], so it is apt that it was named in honor of one of the most prolific and important mathematicians to have lived, Leonhard Euler (pronounced like “oiler”).
A General Note: The Number [latex]e[/latex]
The letter e represents the irrational number
[latex]{\left(1+\frac{1}{n}\right)}^{n},\text{as }n\text{ increases without bound}[/latex]
The letter e is used as a base for many real-world exponential models. To work with base e, we use the approximation, [latex]e\approx 2.718282[/latex]. The constant was named by the Swiss mathematician Leonhard Euler (1707–1783) who first investigated and discovered many of its properties.
Example: Using a Calculator to Find Powers of [latex]e[/latex]
Calculate [latex]{e}^{3.14}[/latex]. Round to five decimal places.
Try It
Use a calculator to find [latex]{e}^{-0.5}[/latex]. Round to five decimal places.
- http://www.worldometers.info/world-population/. Accessed February 24, 2014. ↵
