Learning Outcomes
- Write an explicit formula for an arithmetic sequence.
- Write a recursive formula for the arithmetic sequence.
Using Explicit Formulas for Arithmetic Sequences
We can think of an arithmetic sequence as a function on the domain of the natural numbers; it is a linear function because it has a constant rate of change. The common difference is the constant rate of change, or the slope of the function. We can construct the linear function if we know the slope and the vertical intercept.
[latex]{a}_{n}={a}_{1}+d\left(n - 1\right)[/latex]
To find the y-intercept of the function, we can subtract the common difference from the first term of the sequence. Consider the following sequence.

The common difference is [latex]-50[/latex] , so the sequence represents a linear function with a slope of [latex]-50[/latex] . To find the [latex]y[/latex] -intercept, we subtract [latex]-50[/latex] from [latex]200:200-\left(-50\right)=200+50=250[/latex] . You can also find the [latex]y[/latex] -intercept by graphing the function and determining where a line that connects the points would intersect the vertical axis.

Recall the slope-intercept form of a line is [latex]y=mx+b[/latex]. When dealing with sequences, we use [latex]{a}_{n}[/latex] in place of [latex]y[/latex] and [latex]n[/latex] in place of [latex]x[/latex]. If we know the slope and vertical intercept of the function, we can substitute them for [latex]m[/latex] and [latex]b[/latex] in the slope-intercept form of a line. Substituting [latex]-50[/latex] for the slope and [latex]250[/latex] for the vertical intercept, we get the following equation:
[latex]{a}_{n}=-50n+250[/latex]
sequences as linear functions
We’ve seen several graphs of sequence terms in this module so far. If you think of [latex]n[/latex] representing the input of the function of an arithmetic sequence and [latex]a_n[/latex] as the output of the function, it may help you to better visualize the arithmetic sequence as a linear function of the form [latex]y=mx+b[/latex], or using sequence notation, [latex]a_n=dn+a_0[/latex] where each point on the graph is of the form [latex]\left(n, a_n\right)[/latex] and the common difference gives us the slope of the line.
Note that if we let [latex]n=0[/latex] in the explicit form [latex]a_n=a_1+d(n-1)[/latex], we obtain the statement [latex]a_0=a_1-d[/latex]. That statement tells us that the vertical intercept [latex]a_0[/latex] can be found by subtracting the common difference from the first term.
We do not need to find the vertical intercept to write an explicit formula for an arithmetic sequence. Another explicit formula for this sequence is [latex]{a}_{n}=200 - 50\left(n - 1\right)[/latex] , which simplifies to [latex]{a}_{n}=-50n+250[/latex].
A General Note: Explicit Formula for an Arithmetic Sequence
An explicit formula for the [latex]n\text{th}[/latex] term of an arithmetic sequence is given by
[latex]{a}_{n}={a}_{1}+d\left(n - 1\right)[/latex]
How To: Given the first several terms for an arithmetic sequence, write an explicit formula.
- Find the common difference, [latex]{a}_{2}-{a}_{1}[/latex].
- Substitute the common difference and the first term into [latex]{a}_{n}={a}_{1}+d\left(n - 1\right)[/latex].
Example: Writing the nth Term Explicit Formula for an Arithmetic Sequence
Write an explicit formula for the arithmetic sequence.
[latex]\left\{2\text{, }12\text{, }22\text{, }32\text{, }42\text{, }\ldots \right\}[/latex]
Try It
Write an explicit formula for the following arithmetic sequence.
[latex]\left\{50,47,44,41,\dots \right\}[/latex]
Some arithmetic sequences are defined in terms of the previous term using a recursive formula. The formula provides an algebraic rule for determining the terms of the sequence. A recursive formula allows us to find any term of an arithmetic sequence using a function of the preceding term. Each term is the sum of the previous term and the common difference. For example, if the common difference is 5, then each term is the previous term plus 5. As with any recursive formula, the first term must be given.
[latex]\begin{align}&{a}_{n}={a}_{n - 1}+d && n\ge 2 \end{align}[/latex]
A General Note: Recursive Formula for an Arithmetic Sequence
The recursive formula for an arithmetic sequence with common difference [latex]d[/latex] is:
[latex]\begin{align}&{a}_{n}={a}_{n - 1}+d && n\ge 2 \end{align}[/latex]
How To: Given an arithmetic sequence, write its recursive formula.
- Subtract any term from the subsequent term to find the common difference.
- State the initial term and substitute the common difference into the recursive formula for arithmetic sequences.
tip for success
Either the explicit or the recursive form may be used to describe an arithmetic sequence in which the first term is known. Practice using both of them on the examples in this section.
Example: Writing a Recursive Formula for an Arithmetic Sequence
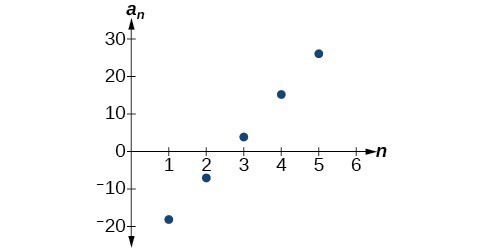
Write a recursive formula for the arithmetic sequence.
[latex]\left\{-18,-7,4,15,26, \ldots \right\}[/latex]
How To: Do we have to subtract the first term from the second term to find the common difference?
No. We can subtract any term in the sequence from the subsequent term. It is, however, most common to subtract the first term from the second term because it is often the easiest method of finding the common difference.
Try It
Write a recursive formula for the arithmetic sequence.
[latex]\left\{25,37,49,61, \dots \right\}[/latex]
Find the Number of Terms in an Arithmetic Sequence
Explicit formulas can be used to determine the number of terms in a finite arithmetic sequence. We need to find the common difference, and then determine how many times the common difference must be added to the first term to obtain the final term of the sequence.
How To: Given the first three terms and the last term of a finite arithmetic sequence, find the total number of terms.
- Find the common difference [latex]d[/latex].
- Substitute the common difference and the first term into [latex]{a}_{n}={a}_{1}+d\left(n - 1\right)[/latex].
- Substitute the last term for [latex]{a}_{n}[/latex] and solve for [latex]n[/latex].
tip for success
Recall that we only need one equation in one unknown to solve for it. Given the explicit form of an arithmetic sequence, [latex]a_n=a_1+d(n-1)[/latex], if we can substitute known values in for all but one component, we can solve for the missing one.
In this case, we are given that a certain finite sequence is arithmetic and we know the first term [latex]a_1[/latex] and the final term [latex]a_n[/latex]. We are able to calculate the common difference from any two consecutive terms, which we are given. Substituting these known values into the explicit formula allows us to solve for the unknown value for the number of terms [latex]n[/latex] without having to generate them.
Example: Finding the Number of Terms in a Finite Arithmetic Sequence
Find the number of terms in the finite arithmetic sequence.
[latex]\left\{8,1,-6, \dots ,-41\right\}[/latex]
Try It
Find the number of terms in the finite arithmetic sequence.
[latex]\left\{6\text{, }11\text{, }16\text{, }...\text{, }56\right\}[/latex]
In the following video lesson, we present a recap of some of the concepts presented about arithmetic sequences up to this point.
Solving Application Problems with Arithmetic Sequences
In many application problems, it often makes sense to use an initial term of [latex]{a}_{0}[/latex] instead of [latex]{a}_{1}[/latex]. In these problems we alter the explicit formula slightly to account for the difference in initial terms. We use the following formula:
[latex]{a}_{n}={a}_{0}+dn[/latex]
Tip for success
See the red box SEQUENCES AS LINEAR FUNCTIONS at the start of this section for a derivation and explanation of this formula.
Keep in mind as you work through the example and practice problems that an arithmetic sequence may be represented as a linear function with input [latex]n[/latex], output [latex]a_n[/latex], and common difference (or slope) of [latex]d[/latex].
Example: Solving Application Problems with Arithmetic Sequences
A five-year old child receives an allowance of $1 each week. His parents promise him an annual increase of $2 per week.
- Write a formula for the child’s weekly allowance in a given year.
- What will the child’s allowance be when he is 16 years old?
Try It
A woman decides to go for a 10-minute run every day this week and plans to increase the time of her daily run by 4 minutes each week. Write a formula for the time of her run after n weeks. How long will her daily run be 8 weeks from today?
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Question ID 29759. Authored by: McClure,Caren. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
- Question ID 23521. Authored by: Shahbazian,Roy, mb McClure,Caren. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Arithmetic Sequences . Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/jExpsJTu9o8. License: CC BY: Attribution