Learning Outcomes
- Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the focal diameter given the equation of a parabola in standard form.
- Find the equation of a parabolic shaped object given dimensions.
Like other graphs we’ve worked with, the graph of a parabola can be translated. If a parabola is translated [latex]h[/latex] units horizontally and [latex]k[/latex] units vertically, the vertex will be [latex]\left(h,k\right)[/latex]. This translation results in the standard form of the equation we saw previously with [latex]x[/latex] replaced by [latex]\left(x-h\right)[/latex] and [latex]y[/latex] replaced by [latex]\left(y-k\right)[/latex].
tip for success
Again, note the familiar transformations of graphs being applied to the translation of the parabola.
To graph parabolas with a vertex [latex]\left(h,k\right)[/latex] other than the origin, we use the standard form [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex] for parabolas that have an axis of symmetry parallel to the x-axis, and [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex] for parabolas that have an axis of symmetry parallel to the y-axis. These standard forms are given below, along with their general graphs and key features.
A General Note: Standard Forms of Parabolas with Vertex (h, k)
The table summarizes the standard features of parabolas with a vertex at a point [latex]\left(h,k\right)[/latex].
| Axis of Symmetry | Equation | Focus | Directrix | Endpoints of focal diameter |
| [latex]y=k[/latex] | [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex] | [latex]\left(h+p,\text{ }k\right)[/latex] | [latex]x=h-p[/latex] | [latex]\left(h+p,\text{ }k\pm 2p\right)[/latex] |
| [latex]x=h[/latex] | [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex] | [latex]\left(h,\text{ }k+p\right)[/latex] | [latex]y=k-p[/latex] | [latex]\left(h\pm 2p,\text{ }k+p\right)[/latex] |
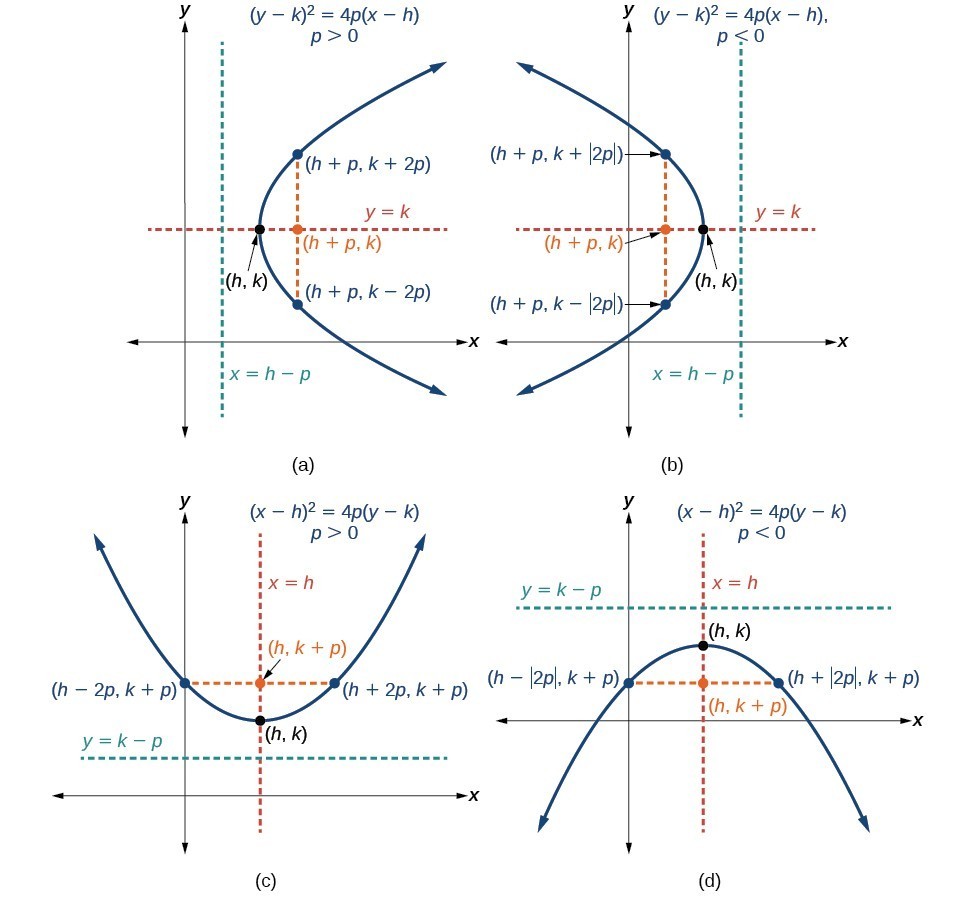
(a) When [latex]p>0[/latex], the parabola opens right. (b) When [latex]p<0[/latex], the parabola opens left. (c) When [latex]p>0[/latex], the parabola opens up. (d) When [latex]p<0[/latex], the parabola opens down.
How To: Given a standard form equation for a parabola centered at (h, k), sketch the graph.
- Determine which of the standard forms applies to the given equation: [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex] or [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex].
- Use the standard form identified in Step 1 to determine the vertex, axis of symmetry, focus, equation of the directrix, and endpoints of the focal diameter.
- If the equation is in the form [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex], then:
- use the given equation to identify [latex]h[/latex] and [latex]k[/latex] for the vertex, [latex]\left(h,k\right)[/latex]
- use the value of [latex]k[/latex] to determine the axis of symmetry, [latex]y=k[/latex]
- set [latex]4p[/latex] equal to the coefficient of [latex]\left(x-h\right)[/latex] in the given equation to solve for [latex]p[/latex]. If [latex]p>0[/latex], the parabola opens right. If [latex]p<0[/latex], the parabola opens left.
- use [latex]h,k[/latex], and [latex]p[/latex] to find the coordinates of the focus, [latex]\left(h+p,\text{ }k\right)[/latex]
- use [latex]h[/latex] and [latex]p[/latex] to find the equation of the directrix, [latex]x=h-p[/latex]
- use [latex]h,k[/latex], and [latex]p[/latex] to find the endpoints of the focal diameter, [latex]\left(h+p,k\pm 2p\right)[/latex]
- If the equation is in the form [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex], then:
- use the given equation to identify [latex]h[/latex] and [latex]k[/latex] for the vertex, [latex]\left(h,k\right)[/latex]
- use the value of [latex]h[/latex] to determine the axis of symmetry, [latex]x=h[/latex]
- set [latex]4p[/latex] equal to the coefficient of [latex]\left(y-k\right)[/latex] in the given equation to solve for [latex]p[/latex]. If [latex]p>0[/latex], the parabola opens up. If [latex]p<0[/latex], the parabola opens down.
- use [latex]h,k[/latex], and [latex]p[/latex] to find the coordinates of the focus, [latex]\left(h,\text{ }k+p\right)[/latex]
- use [latex]k[/latex] and [latex]p[/latex] to find the equation of the directrix, [latex]y=k-p[/latex]
- use [latex]h,k[/latex], and [latex]p[/latex] to find the endpoints of the focal diameter, [latex]\left(h\pm 2p,\text{ }k+p\right)[/latex]
- If the equation is in the form [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex], then:
- Plot the vertex, axis of symmetry, focus, directrix, and focal diameter, and draw a smooth curve to form the parabola.
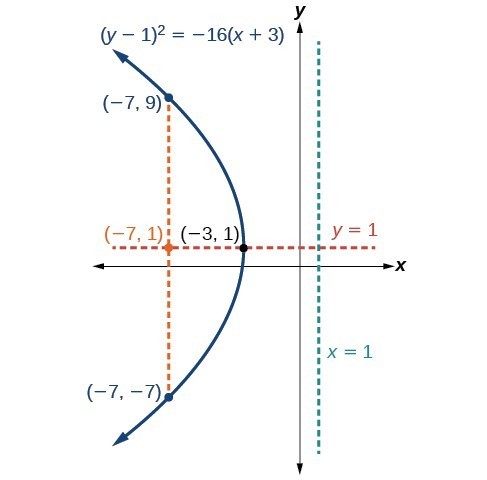
Example: Graphing a Parabola with Vertex (h, k) and Axis of Symmetry Parallel to the x-axis
Graph [latex]{\left(y - 1\right)}^{2}=-16\left(x+3\right)[/latex]. Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the focal diameter.
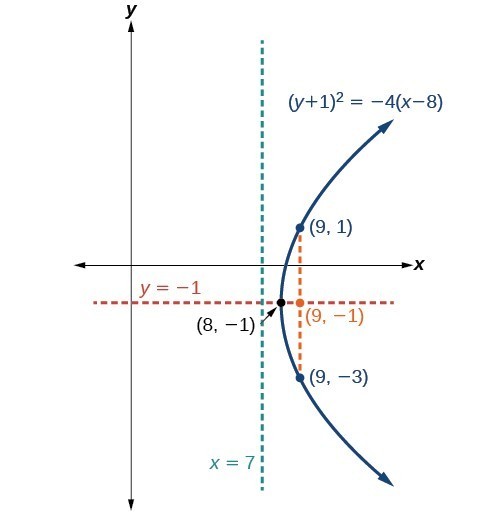
Try It
Graph [latex]{\left(y+1\right)}^{2}=4\left(x - 8\right)[/latex]. Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the focal diameter.
https://ohm.lumenlearning.com/multiembedq.php?id=86148&theme=oea&iframe_resize_id=mom2
recall Complete the square
You will need to complete the square when rewriting the general form of a parabola in the same way you did with the ellipse and hyperbola. Here’s the form to help you.
Completing the Square
Given an expression of the form [latex]a\left(x^2+bx\right)[/latex], add [latex]\left(\dfrac{b}{2}\right)^2[/latex] inside the parentheses, then subtract [latex]a\left(\dfrac{b}{2}\right)^2[/latex] to counteract the change you made.
If completing the square on one side of an equation, you may either subtract the value of [latex]a\left(\dfrac{b}{2}\right)^2[/latex] from that side, or add it to the other to maintain equality.
Then factor the perfect square trinomial you created inside the original parentheses.
Example
[latex]\qquad a\left(x^2+bx\right)[/latex]
[latex]=a\left(x^2+bx+ \left(\dfrac{b}{2}\right)^2\right)-a\left(\dfrac{b}{2}\right)^2[/latex]
[latex]=a\left(x+ \dfrac{b}{2}\right)^2-a\left(\dfrac{b}{2}\right)^2[/latex]
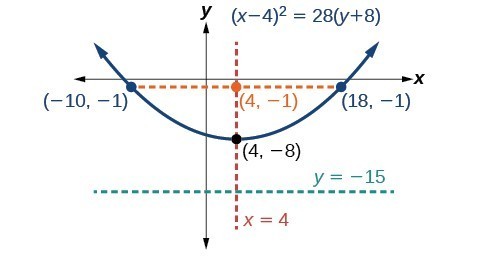
Example: Graphing a Parabola from an Equation Given in General Form
Graph [latex]{x}^{2}-8x - 28y - 208=0[/latex]. Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the focal diameter.
Try It
Graph [latex]{\left(x+2\right)}^{2}=-20\left(y - 3\right)[/latex]. Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the focal diameter.
https://ohm.lumenlearning.com/multiembedq.php?id=86124&theme=oea&iframe_resize_id=mom2
Try It
Use an online graphing tool to graph a parabola whose vertex is [latex](h,k)[/latex].
The equation used to generate the parabola is [latex](y-k)^2 = 4p(x-h)[/latex].
Your task in this exercise is to plot the vertex, axis of symmetry, focus, directrix, and endpoints of the focal diameter in terms of the free variables [latex]h, k, p[/latex].
For example, to plot the vertex, you would create a point [latex](h,k)[/latex].
Solving Applied Problems Involving Parabolas
tip for success
Remember to look for familiar methods and techniques and to find similarities between different types of problems to help you build problem solving skills and intuition.
As we mentioned at the beginning of the section, parabolas are used to design many objects we use every day, such as telescopes, suspension bridges, microphones, and radar equipment. Parabolic mirrors, such as the one used to light the Olympic torch, have a very unique reflecting property. When rays of light parallel to the parabola’s axis of symmetry are directed toward any surface of the mirror, the light is reflected directly to the focus. This is why the Olympic torch is ignited when it is held at the focus of the parabolic mirror.
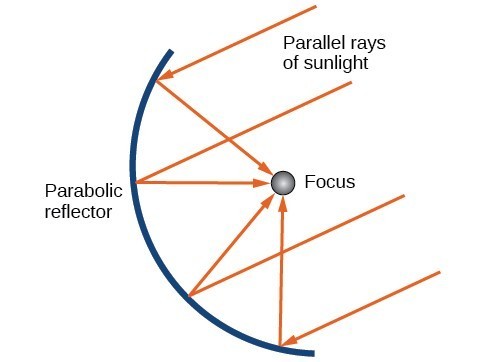
Reflecting property of parabolas
Parabolic mirrors have the ability to focus the sun’s energy to a single point, raising the temperature hundreds of degrees in a matter of seconds. Thus parabolic mirrors are featured in many low-cost, energy efficient solar products, such as solar cookers, solar heaters, and even travel-sized fire starters.
Example: Solving Applied Problems Involving Parabolas
A cross-section of a design for a travel-sized solar fire starter. The sun’s rays reflect off the parabolic mirror toward an object attached to the igniter. Because the igniter is located at the focus of the parabola, the reflected rays cause the object to burn in just seconds.
- Find the equation of the parabola that models the fire starter. Assume that the vertex of the parabolic mirror is the origin of the coordinate plane.
- Use the equation found in part (a) to find the depth of the fire starter.
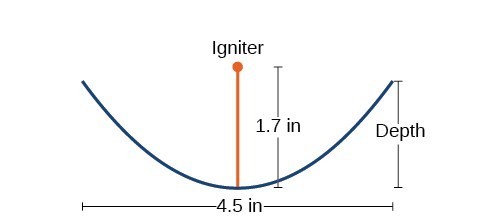
Cross-section of a travel-sized solar fire starter
Try It
Balcony-sized solar cookers have been designed for families living in India. The top of a dish has a diameter of 1600 mm. The sun’s rays reflect off the parabolic mirror toward the “cooker,” which is placed 320 mm from the base.
- Find an equation that models a cross-section of the solar cooker. Assume that the vertex of the parabolic mirror is the origin of the coordinate plane, and that the parabola opens to the right (i.e., has the x-axis as its axis of symmetry).
- Use the equation found in part (a) to find the depth of the cooker.
https://ohm.lumenlearning.com/multiembedq.php?id=87077&theme=oea&iframe_resize_id=mom2
