Learning Outcomes
- Recognize whether a system has one, none, or an infinite number of solutions based on its solution.
- Use correct notation to express solutions to systems of three equations.
Just as with systems of equations in two variables, we may come across an inconsistent system of equations in three variables, which means that it does not have a solution that satisfies all three equations. The equations could represent three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other two but not at the same location. The process of elimination will result in a false statement, such as [latex]3=7[/latex] or some other contradiction.
tip for success
As you discovered when solving systems that have one solution, well-organized work is essential to being certain about the result you obtain. It can take several steps for the contradiction in a system with no solution to appear, as in the example below. Patient effort is essential.
Example: Solving an Inconsistent System of Three Equations in Three Variables
Solve the following system.
[latex]\begin{align}x - 3y+z=4 && \left(1\right) \\ -x+2y - 5z=3 && \left(2\right) \\ 5x - 13y+13z=8 && \left(3\right) \end{align}[/latex]
Watch the video below for another example of using elimination in a system that has no solution.
Try It
Solve the system of three equations in three variables.
[latex]\begin{array}{l}\text{ }x+y+z=2\hfill \\ \text{ }y - 3z=1\hfill \\ 2x+y+5z=0\hfill \end{array}[/latex]
Expressing the Solution of a System of Dependent Equations Containing Three Variables
We know from working with systems of equations in two variables that a dependent system of equations has an infinite number of solutions. The same is true for dependent systems of equations in three variables. An infinite number of solutions can result from several situations. The three planes could be the same, so that a solution to one equation will be the solution to the other two equations. All three equations could be different but they intersect on a line, which has infinite solutions. Or two of the equations could be the same and intersect the third on a line.
tip for success
As you did with dependent two-by-two systems, you can write the general solution to a three-by-three system. See the example below for a demonstration, the try the following problem. It will take practice before it feels natural to write the general solution to a dependent system.
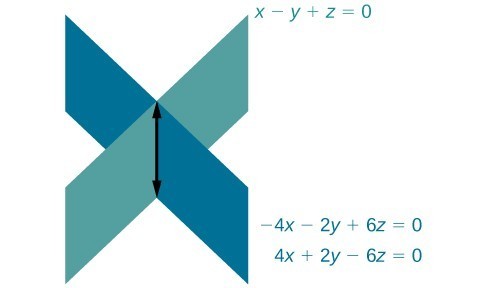
Example: Finding the Solution to a Dependent System of Equations
Find the solution to the given system of three equations in three variables.
[latex]\begin{align}2x+y - 3z=0 && \left(1\right)\\ 4x+2y - 6z=0 && \left(2\right)\\ x-y+z=0 && \left(3\right)\end{align}[/latex]
Q & A
Does the generic solution to a dependent system always have to be written in terms of [latex]x?[/latex]
No, you can write the generic solution in terms of any of the variables, but it is common to write it in terms of [latex]x[/latex] and if needed [latex]x[/latex] and [latex]y[/latex].
See the following video for another example of a dependent three-by-three system.
Try It
Solve the following system.
[latex]\begin{gathered}x+y+z=7 \\ 3x - 2y-z=4 \\ x+6y+5z=24 \end{gathered}[/latex]
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
- Question ID 29695. Authored by: Shahbazian, Roy. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Ex 4: System of Three Equations with Three Unknowns Using Elimination (No Solution).. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/ryNQsWrUoJw. License: CC BY: Attribution
- Ex 5: System of Three Equations with Three Unknowns Using Elimination (Infinite Solutions).. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/mThiwW8nYAU. License: CC BY: Attribution
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution