What you’ll learn to do: Create and evaluate expressions involving polynomials
Earl is building a doghouse whose front is in the shape of a square topped with a triangle. There will be a rectangular door through which the dog can enter and exit the house. Earl wants to find the area of the front of the doghouse so that he can purchase the correct amount of paint. Using the measurements of the front of the house shown in Figure 1 below, we can create an expression that combines several variable terms which allows us to solve this problem and others like it.
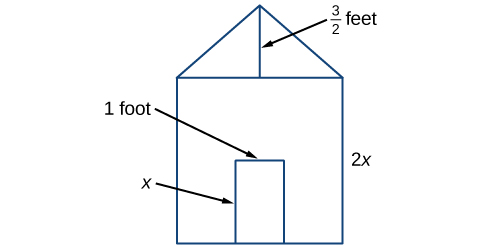
Figure 1
First, find the area of the square in square feet.
Then, find the area of the triangle in square feet.
Next, find the area of the rectangular door in square feet.
The area of the front of the doghouse can be found by adding the areas of the square and the triangle and then subtracting the area of the rectangle. When we do this, we get
[latex]4{x}^{2}+\frac{3}{2}x-x[/latex] ft2, or [latex]4{x}^{2}+\frac{1}{2}x[/latex] ft2.
In this module, we will examine expressions such as this one which combine several variable terms.
