Learning Outcomes
- Solve an Inverse variation problem.
- Write a formula for an inversely proportional relationship.
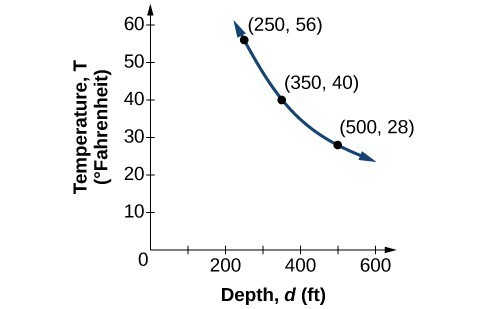
Water temperature in an ocean varies inversely to the water’s depth. Between the depths of 250 feet and 500 feet, the formula [latex]T=\frac{14,000}{d}[/latex] gives us the temperature in degrees Fahrenheit at a depth in feet below Earth’s surface. Consider the Atlantic Ocean, which covers 22% of Earth’s surface. At a certain location, at the depth of 500 feet, the temperature may be 28°F.
If we create a table we observe that, as the depth increases, the water temperature decreases.
| [latex]d[/latex], depth | [latex]T=\frac{\text{14,000}}{d}[/latex] | Interpretation |
|---|---|---|
| 500 ft | [latex]\frac{14,000}{500}=28[/latex] | At a depth of 500 ft, the water temperature is 28° F. |
| 350 ft | [latex]\frac{14,000}{350}=40[/latex] | At a depth of 350 ft, the water temperature is 40° F. |
| 250 ft | [latex]\frac{14,000}{250}=56[/latex] | At a depth of 250 ft, the water temperature is 56° F. |
We notice in the relationship between these variables that, as one quantity increases, the other decreases. The two quantities are said to be inversely proportional and each term varies inversely with the other. Inversely proportional relationships are also called inverse variations.
For our example, the graph depicts the inverse variation. We say the water temperature varies inversely with the depth of the water because, as the depth increases, the temperature decreases. The formula [latex]y=\dfrac{k}{x}[/latex] for inverse variation in this case uses [latex]k=14,000[/latex].
A General Note: Inverse Variation
If [latex]x[/latex] and [latex]y[/latex] are related by an equation of the form
[latex]y=\dfrac{k}{{x}^{n}}[/latex]
where [latex]k[/latex] is a nonzero constant, then we say that [latex]y[/latex] varies inversely with the [latex]n[/latex]th power of [latex]x[/latex]. In inversely proportional relationships, or inverse variations, there is a constant multiple [latex]k={x}^{n}y[/latex].
isolating the constant of variation
To isolate the constant of variation in an inverse variation, use the properties of equality to solve the equation for [latex]k[/latex].
[latex]y=\dfrac{k}{{x}^{n}}[/latex]
Isolate [latex]k[/latex] using algebra.
[latex]yx^n=k[/latex]
Example: Writing a Formula for an Inversely Proportional Relationship
A tourist plans to drive 100 miles. Find a formula for the time the trip will take as a function of the speed the tourist drives.
How To: Given a description of an inverse variation problem, solve for an unknown.
- Identify the input, [latex]x[/latex], and the output, [latex]y[/latex].
- Determine the constant of variation. You may need to multiply [latex]y[/latex] by the specified power of [latex]x[/latex] to determine the constant of variation.
- Use the constant of variation to write an equation for the relationship.
- Substitute known values into the equation to find the unknown.
Example: Solving an Inverse Variation Problem
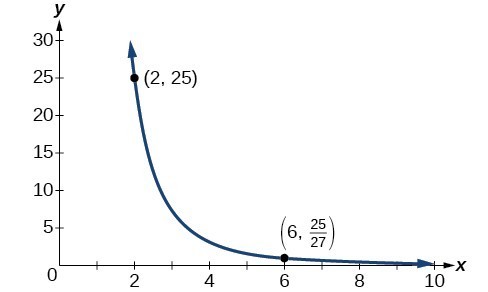
A quantity [latex]y[/latex] varies inversely with the cube of [latex]x[/latex]. If [latex]y=25[/latex] when [latex]x=2[/latex], find [latex]y[/latex] when [latex]x[/latex] is 6.
Try It
A quantity [latex]y[/latex] varies inversely with the square of [latex]x[/latex]. If [latex]y=8[/latex] when [latex]x=3[/latex], find [latex]y[/latex] when [latex]x[/latex] is 4.
https://ohm.lumenlearning.com/multiembedq.php?id=91393&theme=oea&iframe_resize_id=mom1
The following video presents a short lesson on inverse variation and includes more worked examples.
Joint Variation
Many situations are more complicated than a basic direct variation or inverse variation model. One variable often depends on multiple other variables. When a variable is dependent on the product or quotient of two or more variables, this is called joint variation. For example, the cost of busing students for each school trip varies with the number of students attending and the distance from the school. The variable [latex]c[/latex], cost, varies jointly with the number of students, [latex]n[/latex], and the distance, [latex]d[/latex].
A General Note: Joint Variation
Joint variation occurs when a variable varies directly or inversely with multiple variables.
For instance, if [latex]x[/latex] varies directly with both [latex]y[/latex] and [latex]z[/latex], we have [latex]x=kyz[/latex]. If [latex]x[/latex] varies directly with [latex]y[/latex] and inversely with [latex]z[/latex], we have [latex]x=\dfrac{ky}{z}[/latex]. Notice that we only use one constant in a joint variation equation.
isolating the constant of variation
To isolate the constant of variation in a joint variation, use the properties of equality to solve the equation for [latex]k[/latex].
[latex]x=kyz[/latex]
Isolate [latex]k[/latex] using algebra.
[latex]\dfrac{x}{yz}=k[/latex]
Example: Solving Problems Involving Joint Variation
A quantity [latex]x[/latex] varies directly with the square of [latex]y[/latex] and inversely with the cube root of [latex]z[/latex]. If [latex]x=6[/latex] when [latex]y=2[/latex] and [latex]z=8[/latex], find [latex]x[/latex] when [latex]y=1[/latex] and [latex]z=27[/latex].
Try It
[latex]x[/latex] varies directly with the square of [latex]y[/latex] and inversely with [latex]z[/latex]. If [latex]x=40[/latex] when [latex]y=4[/latex] and [latex]z=2[/latex], find [latex]x[/latex] when [latex]y=10[/latex] and [latex]z=25[/latex].
https://ohm.lumenlearning.com/multiembedq.php?id=91394&theme=oea&iframe_resize_id=mom1
The following video provides another worked example of a joint variation problem.