Learning Outcomes
- Solve a logarithmic equation algebraically.
- Solve a logarithmic equation graphically.
- Use the one-to-one property of logarithms to solve a logarithmic equation.
- Solve a radioactive decay problem.
Logarithmic Equations
We have already seen that every logarithmic equation [latex]{\mathrm{log}}_{b}\left(x\right)=y[/latex] is equal to the exponential equation [latex]{b}^{y}=x[/latex]. We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.
For example, consider the equation [latex]{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3[/latex]. To solve this equation, we can use rules of logarithms to rewrite the left side as a single log and then apply the definition of logs to solve for [latex]x[/latex]:
[latex]\begin{array}{l}{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3\hfill & \hfill \\ \text{ }{\mathrm{log}}_{2}\left(2\left(3x - 5\right)\right)=3\hfill & \text{Apply the product rule of logarithms}.\hfill \\ \text{ }{\mathrm{log}}_{2}\left(6x - 10\right)=3\hfill & \text{Distribute}.\hfill \\ \text{ }{2}^{3}=6x - 10\hfill & \text{Convert to exponential form}.\hfill \\ \text{ }8=6x - 10\hfill & \text{Calculate }{2}^{3}.\hfill \\ \text{ }18=6x\hfill & \text{Add 10 to both sides}.\hfill \\ \text{ }x=3\hfill & \text{Divide both sides by 6}.\hfill \end{array}[/latex]
A General Note: Using the Definition of a Logarithm to Solve Logarithmic Equations
For any algebraic expression S and real numbers b and c, where [latex]b>0,\text{ }b\ne 1[/latex],
[latex]{\mathrm{log}}_{b}\left(S\right)=c\text{ if and only if }{b}^{c}=S[/latex]
Example: Using Algebra to Solve a Logarithmic Equation
Solve [latex]2\mathrm{ln}x+3=7[/latex].
tip for success
As was the case when using the properties and rules of exponents and logarithms to rewrite expressions containing them, there can be more than one good way to solve a logarithmic equation. It is good practice to follow the examples given for each of the situations in this section, but you should think about alternative ways to creatively and correctly apply the properties and rules.
Try It
Solve [latex]6+\mathrm{ln}x=10[/latex].
Example: Using Algebra Before and After Using the Definition of the Natural Logarithm
Solve [latex]2\mathrm{ln}\left(6x\right)=7[/latex].
Try It
Solve [latex]2\mathrm{ln}\left(x+1\right)=10[/latex].
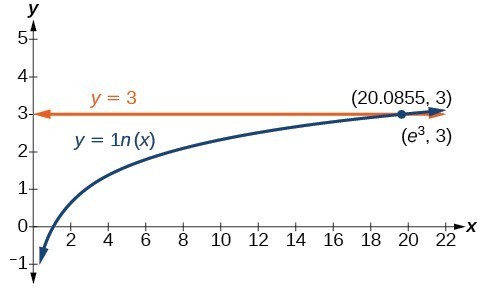
Example: Using a Graph to Understand the Solution to a Logarithmic Equation
Solve [latex]\mathrm{ln}x=3[/latex].
Try It
Use a graphing calculator to estimate the approximate solution to the logarithmic equation [latex]{2}^{x}=1000[/latex] to 2 decimal places.
Using the One-to-One Property of Logarithms to Solve Logarithmic Equations
As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers x > 0, S > 0, T > 0 and any positive real number b, where [latex]b\ne 1[/latex],
[latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\text{ if and only if }S=T[/latex]
For example,
[latex]\text{If }{\mathrm{log}}_{2}\left(x - 1\right)={\mathrm{log}}_{2}\left(8\right),\text{then }x - 1=8[/latex]
So if [latex]x - 1=8[/latex], then we can solve for x and we get x = 9. To check, we can substitute x = 9 into the original equation: [latex]{\mathrm{log}}_{2}\left(9 - 1\right)={\mathrm{log}}_{2}\left(8\right)=3[/latex]. In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.
For example, consider the equation [latex]\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)[/latex]. To solve this equation, we can use the rules of logarithms to rewrite the left side as a single logarithm and then apply the one-to-one property to solve for x:
[latex]\begin{array}{l}\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)\hfill & \hfill \\ \text{}\mathrm{log}\left(\frac{3x - 2}{2}\right)=\mathrm{log}\left(x+4\right)\hfill & \text{Apply the quotient rule of logarithms}.\hfill \\ \text{}\frac{3x - 2}{2}=x+4\hfill & \text{Apply the one-to-one property}.\hfill \\ \text{}3x - 2=2x+8\hfill & \text{Multiply both sides of the equation by }2.\hfill \\ \text{}x=10\hfill & \text{Subtract 2}x\text{ and add 2}.\hfill \end{array}[/latex]
To check the result, substitute x = 10 into [latex]\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)[/latex].
[latex]\begin{array}{l}\mathrm{log}\left(3\left(10\right)-2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(\left(10\right)+4\right)\hfill & \hfill \\ \text{}\mathrm{log}\left(28\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(14\right)\hfill & \hfill \\ \text{}\mathrm{log}\left(\frac{28}{2}\right)=\mathrm{log}\left(14\right)\hfill & \text{The solution checks}.\hfill \end{array}[/latex]
A General Note: Using the One-to-One Property of Logarithms to Solve Logarithmic Equations
For any algebraic expressions S and T and any positive real number b, where [latex]b\ne 1[/latex],
[latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\text{ if and only if }S=T[/latex]
Note, when solving an equation involving logarithms, always check to see if the answer is correct or if it is an extraneous solution.
How To: Given an equation containing logarithms, solve it using the one-to-one property
- Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation is of the form [latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T[/latex].
- Use the one-to-one property to set the arguments equal to each other.
- Solve the resulting equation, S = T, for the unknown.
Example: Solving an Equation Using the One-to-One Property of Logarithms
Solve [latex]\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}\left(2x+3\right)[/latex].
Try It
Solve [latex]\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}1[/latex].
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Question ID 14406. Authored by: Sousa, James. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
- Question ID 122911. Authored by: Lumen Learning. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL