Learning Outcomes
- Use the order of operations to simplify an algebraic expression.
- Use properties of real numbers to simplify algebraic expressions.
When we multiply a number by itself, we square it or raise it to a power of 2. For example, [latex]{4}^{2}=4\cdot 4=16[/latex]. We can raise any number to any power. In general, the exponential notation [latex]{a}^{n}[/latex] means that the number or variable [latex]a[/latex] is used as a factor [latex]n[/latex] times.
In this notation, [latex]{a}^{n}[/latex] is read as the nth power of [latex]a[/latex], where [latex]a[/latex] is called the base and [latex]n[/latex] is called the exponent. A term in exponential notation may be part of a mathematical expression, which is a combination of numbers and operations. For example, [latex]24+6\cdot \frac{2}{3}-{4}^{2}[/latex] is a mathematical expression.
To evaluate a mathematical expression, we perform the various operations. However, we do not perform them in any random order. We use the order of operations. This is a sequence of rules for evaluating such expressions.
Recall that in mathematics we use parentheses ( ), brackets [ ], and braces { } to group numbers and expressions so that anything appearing within the symbols is treated as a unit. Additionally, fraction bars, radicals, and absolute value bars are treated as grouping symbols. When evaluating a mathematical expression, begin by simplifying expressions within grouping symbols.
The next step is to address any exponents or radicals. Afterward, perform multiplication and division from left to right and finally addition and subtraction from left to right.
Let’s take a look at the expression provided.
There are no grouping symbols, so we move on to exponents or radicals. The number 4 is raised to a power of 2, so simplify [latex]{4}^{2}[/latex] as 16.
Next, perform multiplication or division, left to right.
Lastly, perform addition or subtraction, left to right.
Therefore, [latex]24+6\cdot \dfrac{2}{3}-{4}^{2}=12[/latex].
How was the fraction above simplified?
Recall, when mulitplying fractions, we multiply the numerators together and place the result over the product of the denominators.
- [latex]\dfrac{a}{b}\cdot\dfrac{c}{d}=\dfrac{ac}{bd}[/latex]
- [latex]6\cdot\dfrac{2}{3}=\dfrac{6}{1}\cdot\dfrac{2}{3}=\dfrac{12}{3}=4[/latex]
For some complicated expressions, several passes through the order of operations will be needed. For instance, there may be a radical expression inside parentheses that must be simplified before the parentheses are evaluated. Following the order of operations ensures that anyone simplifying the same mathematical expression will get the same result.
A General Note: Order of Operations
Operations in mathematical expressions must be evaluated in a systematic order, which can be simplified using the acronym PEMDAS:
P(arentheses)
E(xponents)
M(ultiplication) and D(ivision)
A(ddition) and S(ubtraction)
How To: Given a mathematical expression, simplify it using the order of operations.
- Simplify any expressions within grouping symbols.
- Simplify any expressions containing exponents or radicals.
- Perform any multiplication and division in order, from left to right.
- Perform any addition and subtraction in order, from left to right.
Example: Using the Order of Operations
Use the order of operations to evaluate each of the following expressions.
- [latex]{\left(3\cdot 2\right)}^{2}-4\left(6+2\right)[/latex]
- [latex]\dfrac{{5}^{2}-4}{7}-\sqrt{11 - 2}[/latex]
- [latex]6-|5 - 8|+3\left(4 - 1\right)[/latex]
- [latex]\dfrac{14 - 3\cdot 2}{2\cdot 5-{3}^{2}}[/latex]
- [latex]7\left(5\cdot 3\right)-2\left[\left(6 - 3\right)-{4}^{2}\right]+1[/latex]
Try It
Use the order of operations to evaluate the following expression:
[latex]\sqrt{(21-17)}-2(7+9^{2})+\dfrac{23-5}{3^2}[/latex]
https://ohm.lumenlearning.com/multiembedq.php?id=259&theme=oea&iframe_resize_id=mom5
https://ohm.lumenlearning.com/multiembedq.php?id=99379&theme=oea&iframe_resize_id=mom11
Watch the following video for more examples of using the order of operations to simplify an expression.
Recall: simplifying fractions
To simplify a fraction, look for common factors in the numerator and the denominator. In the video below, a fraction, [latex]\dfrac{14}{26}[/latex] must be simplified. Since [latex]\dfrac{14}{26}=\dfrac{2\cdot7}{2\cdot13}[/latex], and since [latex]\dfrac{2}{2} = 1[/latex], this fraction simplifies to [latex]\dfrac{7}{13}[/latex].
Using Properties of Real Numbers
For some activities we perform, the order of certain operations does not matter, but the order of other operations does. For example, it does not make a difference if we put on the right shoe before the left or vice-versa. However, it does matter whether we put on shoes or socks first. The same thing is true for operations in mathematics.
Commutative Properties
The commutative property of addition states that numbers may be added in any order without affecting the sum.
We can better see this relationship when using real numbers.
Similarly, the commutative property of multiplication states that numbers may be multiplied in any order without affecting the product.
Again, consider an example with real numbers.
It is important to note that neither subtraction nor division is commutative. For example, [latex]17 - 5[/latex] is not the same as [latex]5 - 17[/latex]. Similarly, [latex]20\div 5\ne 5\div 20[/latex].
Associative Properties
The associative property of multiplication tells us that it does not matter how we group numbers when multiplying. We can move the grouping symbols to make the calculation easier, and the product remains the same.
Consider this example.
The associative property of addition tells us that numbers may be grouped differently without affecting the sum.
This property can be especially helpful when dealing with negative integers. Consider this example.
Are subtraction and division associative? Review these examples.
As we can see, neither subtraction nor division is associative.
Distributive Property
The distributive property states that the product of a factor times a sum is the sum of the factor times each term in the sum.
This property combines both addition and multiplication (and is the only property to do so). Let us consider an example.
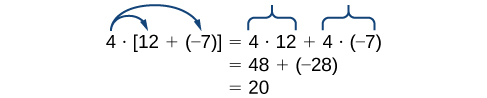
Note that 4 is outside the grouping symbols, so we distribute the 4 by multiplying it by 12, multiplying it by –7, and adding the products.
To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.
Multiplication does not distribute over subtraction, and division distributes over neither addition nor subtraction.
A special case of the distributive property occurs when a sum of terms is subtracted.
For example, consider the difference [latex]12-\left(5+3\right)[/latex]. We can rewrite the difference of the two terms 12 and [latex]\left(5+3\right)[/latex] by turning the subtraction expression into addition of the opposite. So instead of subtracting [latex]\left(5+3\right)[/latex], we add the opposite.
Now, distribute [latex]-1[/latex] and simplify the result.
This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.
Identity Properties
The identity property of addition states that there is a unique number, called the additive identity (0) that, when added to a number, results in the original number.
The identity property of multiplication states that there is a unique number, called the multiplicative identity (1) that, when multiplied by a number, results in the original number.
For example, we have [latex]\left(-6\right)+0=-6[/latex] and [latex]23\cdot 1=23[/latex]. There are no exceptions for these properties; they work for every real number, including 0 and 1.
Inverse Properties
The inverse property of addition states that, for every real number a, there is a unique number, called the additive inverse (or opposite), denoted−a, that, when added to the original number, results in the additive identity, 0.
For example, if [latex]a=-8[/latex], the additive inverse is 8, since [latex]\left(-8\right)+8=0[/latex].
The inverse property of multiplication holds for all real numbers except 0 because the reciprocal of 0 is not defined. The property states that, for every real number a, there is a unique number, called the multiplicative inverse (or reciprocal), denoted [latex]\frac{1}{a}[/latex], that, when multiplied by the original number, results in the multiplicative identity, 1.
For example, if [latex]a=-\frac{2}{3}[/latex], the reciprocal, denoted [latex]\frac{1}{a}[/latex], is [latex]-\frac{3}{2}[/latex] because
A General Note: Properties of Real Numbers
The following properties hold for real numbers a, b, and c.
| Addition | Multiplication | |
|---|---|---|
| Commutative Property | [latex]a+b=b+a[/latex] | [latex]a\cdot b=b\cdot a[/latex] |
| Associative Property | [latex]a+\left(b+c\right)=\left(a+b\right)+c[/latex] | [latex]a\left(bc\right)=\left(ab\right)c[/latex] |
| Distributive Property | [latex]a\cdot \left(b+c\right)=a\cdot b+a\cdot c[/latex] | |
| Identity Property | There exists a unique real number called the additive identity, 0, such that, for any real number a
[latex]a+0=a[/latex]
|
There exists a unique real number called the multiplicative identity, 1, such that, for any real number a
[latex]a\cdot 1=a[/latex]
|
| Inverse Property | Every real number a has an additive inverse, or opposite, denoted –a, such that
[latex]a+\left(-a\right)=0[/latex]
|
Every nonzero real number a has a multiplicative inverse, or reciprocal, denoted [latex]\frac{1}{a}[/latex], such that
[latex]a\cdot \left(\dfrac{1}{a}\right)=1[/latex]
|
Using the Inverse property of numbers: simplifying fractions
Recall when simplifying fractions, we look for common factors in the numerator and denominator to “cancel out.” What we mean by that is that common factors, [latex]\dfrac{a}{a}[/latex], divide to the number 1. This is based on the inverse property of multiplication.
Because the inverse property states that
[latex]a\cdot \left(\dfrac{1}{a}\right)=1[/latex],
and because fraction multiplication gives that
[latex]\dfrac{a}{b}\cdot\dfrac{c}{d} = \dfrac {ac}{bd}[/latex],
We have
[latex]\dfrac{a}{1}\cdot \left(\dfrac{1}{a}\right)=\dfrac{a}{a}=1[/latex]
Example: Using Properties of Real Numbers
Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.
- [latex]3\cdot 6+3\cdot 4[/latex]
- [latex]\left(5+8\right)+\left(-8\right)[/latex]
- [latex]6-\left(15+9\right)[/latex]
- [latex]\dfrac{4}{7}\cdot \left(\frac{2}{3}\cdot \dfrac{7}{4}\right)[/latex]
- [latex]100\cdot \left[0.75+\left(-2.38\right)\right][/latex]
Try It
Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.
- [latex]\left(-\dfrac{23}{5}\right)\cdot \left[11\cdot \left(-\dfrac{5}{23}\right)\right][/latex]
- [latex]5\cdot \left(6.2+0.4\right)[/latex]
- [latex]18-\left(7 - 15\right)[/latex]
- [latex]\dfrac{17}{18}+\cdot \left[\dfrac{4}{9}+\left(-\dfrac{17}{18}\right)\right][/latex]
- [latex]6\cdot \left(-3\right)+6\cdot 3[/latex]
https://ohm.lumenlearning.com/multiembedq.php?id=92360&theme=oea&iframe_resize_id=mom115
https://ohm.lumenlearning.com/multiembedq.php?id=92361&theme=oea&iframe_resize_id=mom120
