Learning Outcomes
- Verify that a radical and a polynomial function are inverses of each other
- Find the inverse of a polynomial function
Recall that two functions [latex]f[/latex] and [latex]g[/latex] are inverse functions if for every coordinate pair in [latex]f[/latex], [latex](a, b)[/latex], there exists a corresponding coordinate pair in the inverse function, [latex]g[/latex], [latex](b, a)[/latex]. In other words, the coordinate pairs of the inverse functions have the input and output interchanged.
Only one-to-one functions have inverses that are also functions. Recall that a one-to-one function has a unique output value for each input value and passes the horizontal line test.
For a function that is not one-to-one to have an inverse function, the function must be restricted on its domain to create a new function that is one-to-one and thus would have an inverse function.
Tip for success
The examples in this section will probably seem confusing at first. The best way to use such examples to study math is to write them out by hand slowly and carefully, perhaps more than once or twice, trying to explain each step to yourself as you work through it. Repeated practice will help you understand the concepts that have been applied in each example.
For example, suppose a water runoff collector is built in the shape of a parabolic trough as shown below. We can use the information in the figure to find the surface area of the water in the trough as a function of the depth of the water.
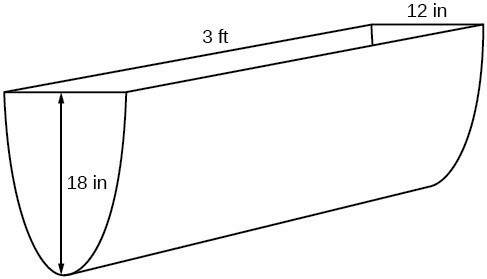
Because it will be helpful to have an equation for the parabolic cross-sectional shape, we will impose a coordinate system at the cross section, with [latex]x[/latex] measured horizontally and [latex]y[/latex] measured vertically, with the origin at the vertex of the parabola.
From this we find an equation for the parabolic shape. We placed the origin at the vertex of the parabola, so we know the equation will have form [latex]y\left(x\right)=a{x}^{2}[/latex]. Our equation will need to pass through the point (6, 18), from which we can solve for the stretch factor [latex]a[/latex].
[latex]\begin{align} 18&=a{6}^{2} \\[1mm] a&=\frac{18}{36} \\[1mm] a&=\frac{1}{2} \end{align}[/latex]
Our parabolic cross section has the equation
[latex]y\left(x\right)=\frac{1}{2}{x}^{2}[/latex]
We are interested in the surface area of the water, so we must determine the width at the top of the water as a function of the water depth. For any depth [latex]y[/latex] the width will be given by [latex]2x[/latex], so we need to solve the equation above for [latex]x[/latex] and find the inverse function. However, notice that the original function is not one-to-one, and indeed, given any output there are two inputs that produce the same output, one positive and one negative.
To find an inverse, we can restrict our original function to a limited domain on which it is one-to-one. In this case, it makes sense to restrict ourselves to positive [latex]x[/latex] values. On this domain, we can find an inverse by solving for the input variable:
[latex]\begin{align}y&=\frac{1}{2}{x}^{2} \\[1mm] 2y&={x}^{2} \\[1mm] x&=\pm \sqrt{2y} \end{align}[/latex]
This is not a function as written. We are limiting ourselves to positive [latex]x[/latex] values, so we eliminate the negative solution, giving us the inverse function we’re looking for.
[latex]y=\dfrac{{x}^{2}}{2},\text{ }x>0[/latex]
Because [latex]x[/latex] is the distance from the center of the parabola to either side, the entire width of the water at the top will be [latex]2x[/latex]. The trough is 3 feet (36 inches) long, so the surface area will then be:
[latex]\begin{align}\text{Area} &=l\cdot w \\[1mm] &=36\cdot 2x \\[1mm] &=72x \\[1mm] &=72\sqrt{2y} \end{align}[/latex]
This example illustrates two important points:
- When finding the inverse function of a quadratic, we have to limit ourselves to a domain on which the function is one-to-one.
- The inverse function of a quadratic function is a square root function. Both are toolkit functions and different types of power functions.
Functions involving roots are often called radical functions. While it is not possible to find an inverse function of most polynomial functions, some basic polynomials do have inverses that are functions. Such functions are called invertible functions, and we use the notation [latex]{f}^{-1}\left(x\right)[/latex].
Warning: [latex]{f}^{-1}\left(x\right)[/latex] is not the same as the reciprocal of the function [latex]f\left(x\right)[/latex]. This use of –1 is reserved to denote inverse functions. To denote the reciprocal of a function [latex]f\left(x\right)[/latex], we would need to write [latex]{\left(f\left(x\right)\right)}^{-1}=\frac{1}{f\left(x\right)}[/latex].
An important relationship between inverse functions is that they “undo” each other. If [latex]{f}^{-1}[/latex] is the inverse of a function [latex]f[/latex], then [latex]f[/latex] is the inverse of the function [latex]{f}^{-1}[/latex]. In other words, whatever the function [latex]f[/latex] does to [latex]x[/latex], [latex]{f}^{-1}[/latex] undoes it—and vice-versa. More formally, we write
[latex]{f}^{-1}\left(f\left(x\right)\right)=x,\text{for all }x\text{ in the domain of }f[/latex]
and
[latex]f\left({f}^{-1}\left(x\right)\right)=x,\text{for all }x\text{ in the domain of }{f}^{-1}[/latex]
A General Note: Verifying Two Functions Are Inverses of One Another
Two functions, [latex]f[/latex] and [latex]g[/latex], are inverses of one another if for all [latex]x[/latex] in the domain of [latex]f[/latex] and [latex]g[/latex].
[latex]g\left(f\left(x\right)\right)=f\left(g\left(x\right)\right)=x[/latex]
How To: Given a polynomial function, find the inverse of the function by restricting the domain in such a way that the new function is one-to-one.
- Verify that [latex]f[/latex] is a one-to-one function.
- Replace [latex]f\left(x\right)[/latex] with [latex]y[/latex].
- Interchange [latex]x[/latex] and [latex]y[/latex].
- Solve for [latex]y[/latex], and rename the function [latex]{f}^{-1}\left(x\right)[/latex].
Example: Verifying Inverse Functions
Show that [latex]f\left(x\right)=\dfrac{1}{x+1}[/latex] and [latex]{f}^{-1}\left(x\right)=\dfrac{1}{x}-1[/latex] are inverses, for [latex]x\ne 0,-1[/latex] .
Try It
Show that [latex]f\left(x\right)=\dfrac{x+5}{3}[/latex] and [latex]{f}^{-1}\left(x\right)=3x - 5[/latex] are inverses.
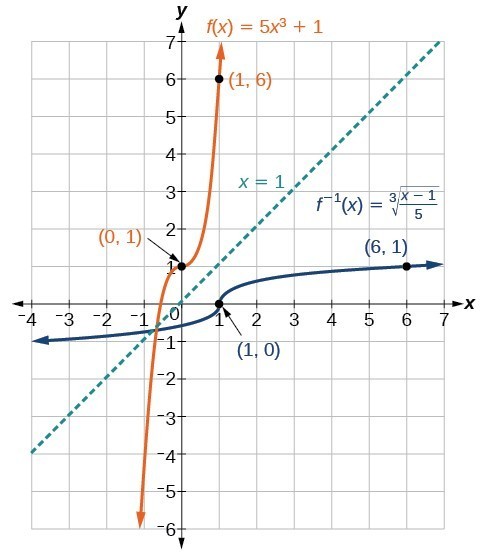
Example: Finding the Inverse of a Cubic Function
Find the inverse of the function [latex]f\left(x\right)=5{x}^{3}+1[/latex].
Try It
Find the inverse function of [latex]f\left(x\right)=\sqrt[3]{x+4}[/latex].
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Question ID 15856. Authored by: Sousa,James. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2