Learning Outcomes
- Identify binomial coefficients given the formula for a combination.
- Expand a binomial using the binomial theorem.
- Use the binomial to find a single term in a binomial.
expanding [latex]\left(x+y\right)^n[/latex]
Earlier, we learned how to use the distributive property to multiply binomials together. We found that certain binomial products resulted in a nice pattern such as [latex](a+b)^2 = a^2 + 2ab + b^2[/latex]. But multiplying more than three binomials together was a tedious process.
We will learn now that there is a pattern we can apply to greater powers of binomial factors.
Previously, we studied combinations. In the shortcut to finding [latex]{\left(x+y\right)}^{n}[/latex], we will need to use combinations to find the coefficients that will appear in the expansion of the binomial. In this case, we use the notation [latex]\left(\begin{gathered}n\\ r\end{gathered}\right)[/latex] instead of [latex]C\left(n,r\right)[/latex], but it can be calculated in the same way. So
[latex]\left(\begin{gathered}n\\ r\end{gathered}\right)=C\left(n,r\right)=\dfrac{n!}{r!\left(n-r\right)!}[/latex]
The combination [latex]\left(\begin{gathered}n\\ r\end{gathered}\right)[/latex] is called a binomial coefficient. An example of a binomial coefficient is [latex]\left(\begin{gathered}5\\ 2\end{gathered}\right)=C\left(5,2\right)=10[/latex].
A General Note: Binomial Coefficients
If [latex]n[/latex] and [latex]r[/latex] are integers greater than or equal to 0 with [latex]n\ge r[/latex], then the binomial coefficient is
[latex]\left(\begin{gathered}n\\ r\end{gathered}\right)=C\left(n,r\right)=\dfrac{n!}{r!\left(n-r\right)!}[/latex]
Q & A
Is a binomial coefficient always a whole number?
Yes. Just as the number of combinations must always be a whole number, a binomial coefficient will always be a whole number.
Example: Finding Binomial Coefficients
Find each binomial coefficient.
- [latex]\left(\begin{gathered}5\\ 3\end{gathered}\right)[/latex]
- [latex]\left(\begin{gathered}9\\ 2\end{gathered}\right)[/latex]
- [latex]\left(\begin{gathered}9\\ 7\end{gathered}\right)[/latex]
Try It
Find each binomial coefficient.
- [latex]\left(\begin{gathered}7\\ 3\end{gathered}\right)[/latex]
- [latex]\left(\begin{gathered}11\\ 4\end{gathered}\right)[/latex]
tip for success
The patterns that emerge from calculating binomial coefficients and that are present in Pascal’s Triangle are handy and should be memorized over time as mathematical facts much in the same way that you just “know” [latex]4[/latex] and [latex]3[/latex] make [latex]7[/latex]. Of course, that will take a lot of time and patient practice. If you are continuing in mathematics beyond this course, it will be well worth the effort.
Start by working through the next several paragraphs and the examples that follow on paper, perhaps more than once or twice, to begin to get familiar with the patterns and processes. Don’t be discouraged if it takes time to become clear. It is a challenging concept.
When we expand [latex]{\left(x+y\right)}^{n}[/latex] by multiplying, the result is called a binomial expansion, and it includes binomial coefficients. If we wanted to expand [latex]{\left(x+y\right)}^{52}[/latex], we might multiply [latex]\left(x+y\right)[/latex] by itself fifty-two times. This could take hours! If we examine some simple binomial expansions, we can find patterns that will lead us to a shortcut for finding more complicated binomial expansions.
[latex]\begin{align}&{\left(x+y\right)}^{2}={x}^{2}+2xy+{y}^{2} \\ &{\left(x+y\right)}^{3}={x}^{3}+3{x}^{2}y+3x{y}^{2}+{y}^{3} \\ &{\left(x+y\right)}^{4}={x}^{4}+4{x}^{3}y+6{x}^{2}{y}^{2}+4x{y}^{3}+{y}^{4} \end{align}[/latex]
First, let’s examine the exponents. With each successive term, the exponent for [latex]x[/latex] decreases and the exponent for [latex]y[/latex] increases. The sum of the two exponents is [latex]n[/latex] for each term.
Next, let’s examine the coefficients. Notice that the coefficients increase and then decrease in a symmetrical pattern. The coefficients follow a pattern:
[latex]\left(\begin{gathered}n\\ 0\end{gathered}\right),\left(\begin{gathered}n\\ 1\end{gathered}\right),\left(\begin{gathered}n\\ 2\end{gathered}\right),\dots,\left(\begin{gathered}n\\ n\end{gathered}\right)[/latex].
These patterns lead us to the Binomial Theorem, which can be used to expand any binomial.
[latex]\begin{align}{\left(x+y\right)}^{n}& =\sum\limits _{k=0}^{n}\left(\begin{gathered}n\\ k\end{gathered}\right){x}^{n-k}{y}^{k} \\ & ={x}^{n}+\left(\begin{gathered}n\\ 1\end{gathered}\right){x}^{n - 1}y+\left(\begin{gathered}{c}n\\ 2\end{gathered}\right){x}^{n - 2}{y}^{2}+\dots+\left(\begin{gathered}n\\ n - 1\end{gathered}\right)x{y}^{n - 1}+{y}^{n} \end{align}[/latex]
Another way to see the coefficients is to examine the expansion of a binomial in general form, [latex]x+y[/latex], to successive powers 1, 2, 3, and 4.
[latex]\begin{align}&{\left(x+y\right)}^{1}=x+y \\ &{\left(x+y\right)}^{2}={x}^{2}+2xy+{y}^{2} \\ &{\left(x+y\right)}^{3}={x}^{3}+3{x}^{2}y+3x{y}^{2}+{y}^{3} \\ &{\left(x+y\right)}^{4}={x}^{4}+4{x}^{3}y+6{x}^{2}{y}^{2}+4x{y}^{3}+{y}^{4} \end{align}[/latex]
Can you guess the next expansion for the binomial [latex]{\left(x+y\right)}^{5}?[/latex]

Above is an illustration the following:
- There are [latex]n+1[/latex] terms in the expansion of [latex]{\left(x+y\right)}^{n}[/latex].
- The degree (or sum of the exponents) for each term is [latex]n[/latex].
- The powers on [latex]x[/latex] begin with [latex]n[/latex] and decrease to 0.
- The powers on [latex]y[/latex] begin with 0 and increase to [latex]n[/latex].
- The coefficients are symmetric.
To determine the expansion on [latex]{\left(x+y\right)}^{5}[/latex], we see [latex]n=5[/latex], thus, there will be 5+1 = 6 terms. Each term has a combined degree of 5. In descending order for powers of [latex]x[/latex], the pattern is as follows:
- Introduce [latex]{x}^{5}[/latex], and then for each successive term reduce the exponent on [latex]x[/latex] by 1 until [latex]{x}^{0}=1[/latex] is reached.
- Introduce [latex]{y}^{0}=1[/latex], and then increase the exponent on [latex]y[/latex] by 1 until [latex]{y}^{5}[/latex] is reached.
[latex]{x}^{5},{x}^{4}y,{x}^{3}{y}^{2},{x}^{2}{y}^{3},x{y}^{4},{y}^{5}[/latex]
The next expansion would be
[latex]{\left(x+y\right)}^{5}={x}^{5}+5{x}^{4}y+10{x}^{3}{y}^{2}+10{x}^{2}{y}^{3}+5x{y}^{4}+{y}^{5}[/latex].
But where do those coefficients come from? The binomial coefficients are symmetric. We can see these coefficients in an array known as Pascal’s Triangle.
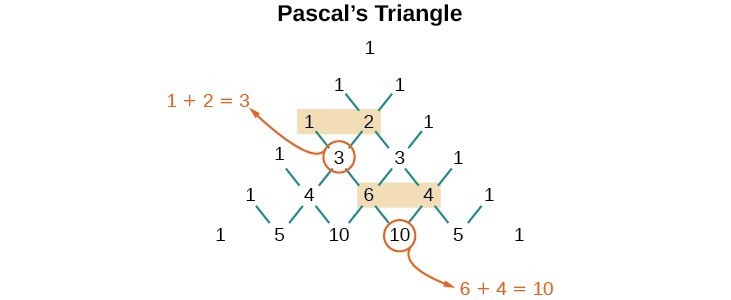
To generate Pascal’s Triangle, we start by writing a 1. In the row below, row 2, we write two 1’s. In the 3rd row, flank the ends of the rows with 1’s, and add [latex]1+1[/latex] to find the middle number, 2. In the [latex]n\text{th}[/latex] row, flank the ends of the row with 1’s. Each element in the triangle is the sum of the two elements immediately above it.
To see the connection between Pascal’s Triangle and binomial coefficients, let us revisit the expansion of the binomials in general form.
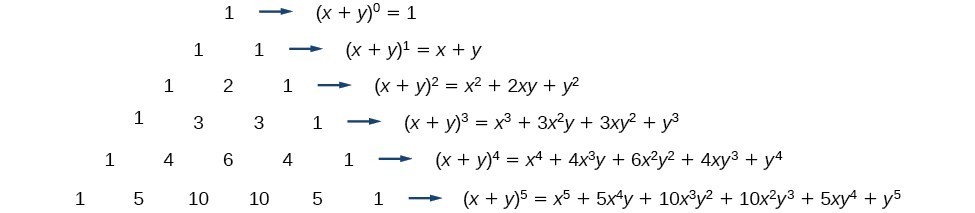
A General Note: The Binomial Theorem
The Binomial Theorem is a formula that can be used to expand any binomial.
[latex]\begin{align}{\left(x+y\right)}^{n}& =\sum\limits _{k=0}^{n}\left(\begin{gathered}n\\ k\end{gathered}\right){x}^{n-k}{y}^{k} \\ & ={x}^{n}+\left(\begin{gathered}n\\ 1\end{gathered}\right){x}^{n - 1}y+\left(\begin{gathered}{c}n\\ 2\end{gathered}\right){x}^{n - 2}{y}^{2}+\dots+\left(\begin{gathered}n\\ n - 1\end{gathered}\right)x{y}^{n - 1}+{y}^{n} \end{align}[/latex]
How To: Given a binomial, write it in expanded form.
- Determine the value of [latex]n[/latex] according to the exponent.
- Evaluate the [latex]k=0[/latex] through [latex]k=n[/latex] using the Binomial Theorem formula.
- Simplify.
tip for success
Remember to try the examples and practice problems before looking at the answers!
Example: Expanding a Binomial
Write in expanded form.
- [latex]{\left(x+y\right)}^{5}[/latex]
- [latex]{\left(3x-y\right)}^{4}[/latex]
Try It
Write in expanded form.
- [latex]{\left(x-y\right)}^{5}[/latex]
- [latex]{\left(2x+5y\right)}^{3}[/latex]
https://ohm.lumenlearning.com/multiembedq.php?id=156714&theme=oea&iframe_resize_id=mom1
Using the Binomial Theorem to Find a Single Term
Expanding a binomial with a high exponent such as [latex]{\left(x+2y\right)}^{16}[/latex] can be a lengthy process.
Sometimes we are interested only in a certain term of a binomial expansion. We do not need to fully expand a binomial to find a single specific term.
Note the pattern of coefficients in the expansion of [latex]{\left(x+y\right)}^{5}[/latex].
[latex]{\left(x+y\right)}^{5}={x}^{5}+\left(\begin{gathered}5\\ 1\end{gathered}\right){x}^{4}y+\left(\begin{gathered}5\\ 2\end{gathered}\right){x}^{3}{y}^{2}+\left(\begin{gathered}5\\ 3\end{gathered}\right){x}^{2}{y}^{3}+\left(\begin{gathered}5\\ 4\end{gathered}\right)x{y}^{4}+{y}^{5}[/latex]
The second term is [latex]\left(\begin{gathered}5\\ 1\end{gathered}\right){x}^{4}y[/latex]. The third term is [latex]\left(\begin{gathered}5\\ 2\end{gathered}\right){x}^{3}{y}^{2}[/latex]. We can generalize this result.
[latex]\left(\begin{gathered}n\\ r\end{gathered}\right){x}^{n-r}{y}^{r}[/latex]
A General Note: The (r+1)th Term of a Binomial Expansion
The [latex]\left(r+1\right)\text{th}[/latex] term of the binomial expansion of [latex]{\left(x+y\right)}^{n}[/latex] is:
[latex]\left(\begin{gathered}n\\ r\end{gathered}\right){x}^{n-r}{y}^{r}[/latex]
How To: Given a binomial, write a specific term without fully expanding.
- Determine the value of [latex]n[/latex] according to the exponent.
- Determine [latex]\left(r+1\right)[/latex].
- Determine [latex]r[/latex].
- Replace [latex]r[/latex] in the formula for the [latex]\left(r+1\right)\text{th}[/latex] term of the binomial expansion.
tip for success
No peeking! Remember to try the examples and practice problems before looking at the answers.
Example: Writing a Given Term of a Binomial Expansion
Find the tenth term of [latex]{\left(x+2y\right)}^{16}[/latex] without fully expanding the binomial.
Try It
Find the sixth term of [latex]{\left(3x-y\right)}^{9}[/latex] without fully expanding the binomial.
