Correlational Research

One of the primary methods used to study abnormal behavior is the correlational method. Correlation means that there is a relationship between two or more variables (such between the variables of negative thinking and depressive symptoms), but this relationship does not necessarily imply cause and effect. When two variables are correlated, it simply means that as one variable changes, so does the other. We can measure correlation by calculating a statistic known as a correlation coefficient. A correlation coefficient is a number from negative one to positive one that indicates the strength and direction of the relationship between variables. The association between two variables can be summarized statistically using the correlation coefficient (abbreviated as r).

The number portion of the correlation coefficient indicates the strength of the relationship. The closer the number is to one (be it negative or positive), the more strongly related the variables are, and the more predictable changes in one variable will be as the other variable changes. The closer the number is to zero, the weaker the relationship, and the less predictable the relationships between the variables becomes. For instance, a correlation coefficient of 0.9 indicates a far stronger relationship than a correlation coefficient of 0.3. If the variables are not related to one another at all, the correlation coefficient is zero. The example above about negative thinking and depressive symptoms is an example of two variables that we might expect to have a relationship to each other. When higher values in one variable (negative thinking) are associated with higher values in the other variable (depressive symptoms), there is a positive correlation between the variables.

The sign—positive or negative—of the correlation coefficient indicates the direction of the relationship. Positive correlations carry positive signs; negative correlations carry negative signs. A positive correlation means that the variables move in the same direction. Put another way, it means that as one variable increases so does the other, and conversely, when one variable decreases so does the other. A negative correlation means that the variables move in opposite directions. If two variables are negatively correlated, a decrease in one variable is associated with an increase in the other and vice versa.

Other examples of positive correlations are the relationship between depression and disturbance in normal sleep patterns. One might expect then that scores on a measure of depression would be positively correlated with scores on a measure of sleep disturbances.

One might expect a negative correlation to exist between between depression and self-esteem. The more depressed people are, the lower their scores are on the Rosenberg self-esteem scale (RSES), a self-esteem measure widely used in social-science research. Keep in mind that a negative correlation is not the same as no correlation. For example, we would probably find no correlation between depression and someone’s height. 

In correlational research, scientists passively observe and measure phenomena.  Here, we do not intervene and change behavior, as we do in experiments. In correlational research, we identify patterns of relationships, but we usually cannot infer what causes what. Importantly, with correlational research, you can examine only two variables at a time, no more and no less.

As mentioned earlier, correlations have predictive value. So, what if you wanted to test whether spending on others is related to happiness, but you don’t have $20 to give to each participant? You could use a correlational design—which is exactly what Professor Dunn did, too. She asked people how much of their income they spent on others or donated to charity, and later she asked them how happy they were. Do you think these two variables were related? Yes, they were! The more money people reported spending on others, the happier they were.

More Details about the Correlation

To find out how well two variables correspond, we can plot the relationship between the two scores on what is known as a scatterplot (Figure 1). In the scatterplot, each dot represents a data point. (In this case it’s individuals, but it could be some other unit.) Importantly, each dot provides us with two pieces of information—in this case, information about how good the person rated the past month (x-axis) and how happy the person felt in the past month (y-axis). Which variable is plotted on which axis does not matter.

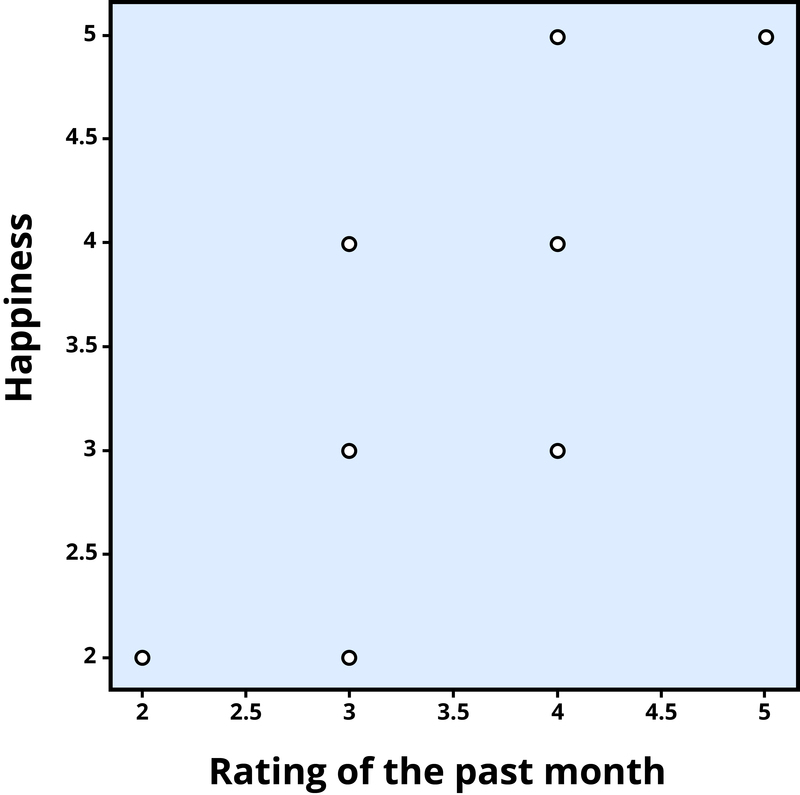
Figure 1. Scatterplot of the association between happiness and ratings of the past month, a positive correlation (r = .81). Each dot represents an individual.

For the example above, the direction of the association is positive. This means that people who perceived the past month as being good reported feeling more happy, whereas people who perceived the month as being bad reported feeling less happy.

In a scatterplot, the dots form a pattern that extends from the bottom left to the upper right (just as they do in Figure 1). The r value for a positive correlation is indicated by a positive number (although, the positive sign is usually omitted). Here, the r value is 0.81.

Figure 2 shows a negative correlation, the association between the average height of males in a country (y-axis) and the pathogen prevalence, or commonness of disease, of that country (x-axis). In this scatterplot, each dot represents a country. Notice how the dots extend from the top left to the bottom right. What does this mean in real-world terms? It means that people are shorter in parts of the world where there is more disease. The r value for a negative correlation is indicated by a negative number—that is, it has a minus (−) sign in front of it. Here, it is −0.83.

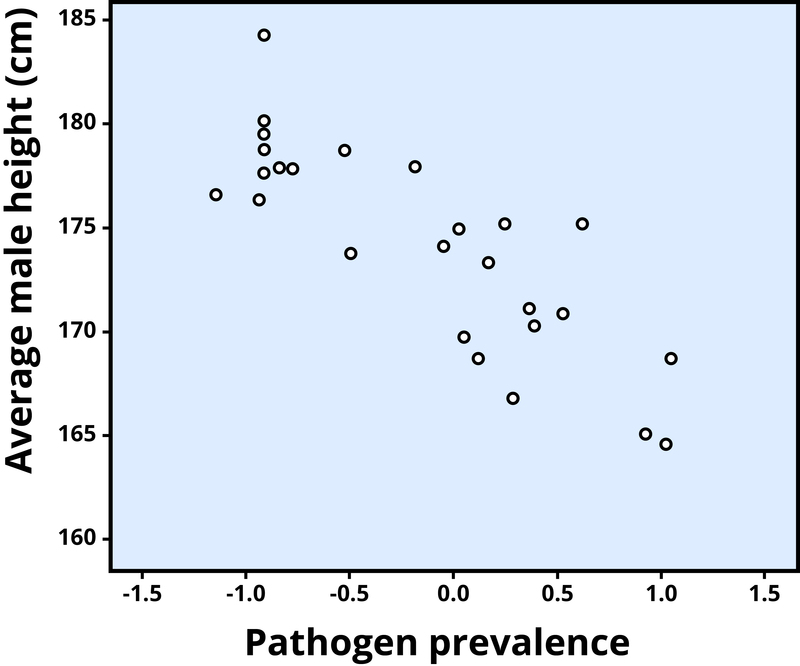
Figure 2. Scatterplot showing the association between average male height and pathogen prevalence, a negative correlation (r = –0.83). Each dot represents a country (Chiao, 2009).

The strength of a correlation has to do with how well the two variables align. Recall that in Professor Dunn’s correlational study, spending on others positively correlated with happiness: the more money people reported spending on others, the happier they reported to be. At this point, you may be thinking to yourself, “I know a very generous person who gave away lots of money to other people but is miserable!” Or maybe you know of a very stingy person who is happy as can be. Yes, there might be exceptions. If an association has many exceptions, it is considered a weak correlation. If an association has few or no exceptions, it is considered a strong correlation. A strong correlation is one in which the two variables always, or almost always, go together. In the example of happiness and how good the month has been, the association is strong. The stronger a correlation is, the tighter the dots in the scatterplot will be arranged along a sloped line.^[1]