Place Value in Whole Numbers

Learning Objectives

  • Use place value to define all digits of a whole number

Our number system is called a place value system because the value of a digit depends on its position, or place, in a number. The number [latex]537[/latex] has a different value than the number [latex]735[/latex]. Even though they use the same digits, their value is different because of the different placement of the [latex]3[/latex] and the [latex]7[/latex] and the [latex]5[/latex].

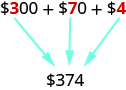
Money gives us a familiar model of place value. Suppose a wallet contains three $100 bills, seven $10 bills, and four $1 bills. The amounts are summarized in the image below. How much money is in the wallet?

An image of three stacks of American currency. First stack from left to right is a stack of 3 $100 bills, then a stack of 7 $10 bills, then a stack of 4 $1 bills. 3 time $100 equals $300, 7 times $10 equals $70, and 4 times $1 equals $4.
Find the total value of each kind of bill, and then add to find the total. The wallet contains $374.

$300 plus $70 plus $4 equals $374
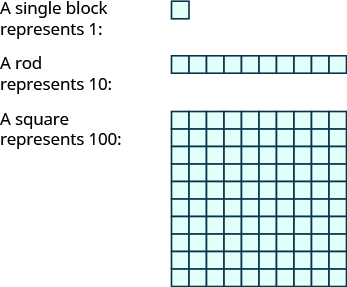
Base-10 blocks provide another way to model place value, as shown in the image below. The blocks can be used to represent hundreds, tens, and ones. Notice that the tens rod is made up of [latex]10[/latex] ones, and the hundreds square is made of [latex]10[/latex] tens, or [latex]100[/latex] ones.

An image with three items. The first item is a single block with the label "A single block represents 1". The second item is row of ten squares with the label "A rod represents 10". The third items is a square made up of smaller squares with the label "A square represents 100".
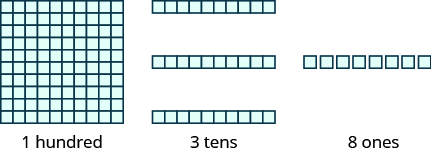
The image below shows the number [latex]138[/latex] modeled with base-10 blocks.

We use place value notation to show the value of the number [latex]138[/latex].

An image consisting of three items. The first item is a square of 100 blocks, 10 blocks wide and 10 blocks tall, with the label 1 hundred. Then 3 separate rows of squares with the label 3 tens. Then 8 single squares with the label 8 ones.

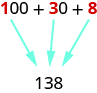
The equation 100 plus 30 plus 8. Taking the hundredth's, tenth's and one's place from each number, respectively, the sum is 138.

Digit Place value Number Value Total value
[latex]1[/latex] hundreds [latex]1[/latex] [latex]100[/latex] [latex]100\phantom{\rule{1 em}{0ex}}[/latex]
[latex]3[/latex] tens [latex]3[/latex] [latex]10[/latex] [latex]30\phantom{\rule{1 em}{0ex}}[/latex]
[latex]8[/latex] ones [latex]8[/latex] [latex]1[/latex] [latex]+\phantom{\rule{.5 em}{0ex}}8\phantom{\rule{1 em}{0ex}}[/latex]
[latex]\text{Sum =}138\phantom{\rule{1 em}{0ex}}[/latex]

example

Use place value notation to find the value of the number modeled by the base-10 blocks shown.

An image consisting of three items. The first item is two squares of 100 blocks each, 10 blocks wide and 10 blocks tall. The second item is one horizontal rod containing 10 blocks. The third item is 5 individual blocks.

Try it

By looking at money and base-[latex]10[/latex] blocks, we saw that each place in a number has a different value. A place value chart is a useful way to summarize this information. The place values are separated into groups of three, called periods. The periods are ones, thousands, millions, billions, trillions, and so on. In a written number, commas separate the periods.

Just as with the base-[latex]10[/latex] blocks, where the value of the tens rod is ten times the value of the ones block and the value of the hundreds square is ten times the tens rod, the value of each place in the place-value chart is ten times the value of the place to the right of it.

The chart below shows how the number [latex]5,278,194[/latex] is written in a place value chart.

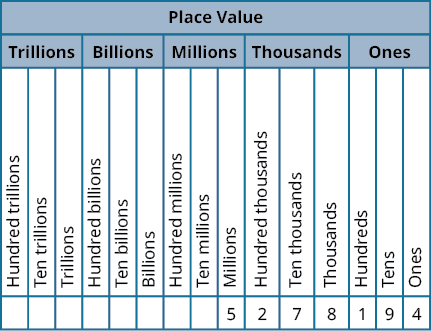
A chart titled 'Place Value' with fifteen columns and 4 rows, with the columns broken down into five groups of three. The header row shows Trillions, Billions, Millions, Thousands, and Ones. The next row has the values 'Hundred trillions', 'Ten trillions', 'trillions', 'hundred billions', 'ten billions', 'billions', 'hundred millions', 'ten millions', 'millions', 'hundred thousands', 'ten thousands', 'thousands', 'hundreds', 'tens', and 'ones'. The first 8 values in the next row are blank. Starting with the ninth column, the values are '5', '2', '7', '8', '1', '9', and '4'.

  • The digit [latex]5[/latex] is in the millions place. Its value is [latex]5,000,000[/latex].
  • The digit [latex]2[/latex] is in the hundred thousands place. Its value is [latex]200,000[/latex].
  • The digit [latex]7[/latex] is in the ten thousands place. Its value is [latex]70,000[/latex].
  • The digit [latex]8[/latex] is in the thousands place. Its value is [latex]8,000[/latex].
  • The digit [latex]1[/latex] is in the hundreds place. Its value is [latex]100[/latex].
  • The digit [latex]9[/latex] is in the tens place. Its value is [latex]90[/latex].
  • The digit [latex]4[/latex] is in the ones place. Its value is [latex]4[/latex].

example

In the number [latex]63,407,218[/latex]; find the place value of each of the following digits:

  1. [latex]7[/latex]
  2. [latex]0[/latex]
  3. [latex]1[/latex]
  4. [latex]6[/latex]
  5. [latex]3[/latex]

try it

The video below shows more examples of how to determine the place value of a digit in a number.