Using the Pythagorean Theorem to Solve Problems

Learning Outcomes

Use the Pythagorean theorem to find the unknown side length of a right triangle

The Pythagorean theorem is a special property of right triangles that has been used since ancient times. It is named after the Greek philosopher and mathematician Pythagoras who lived around [latex]500[/latex] BCE.

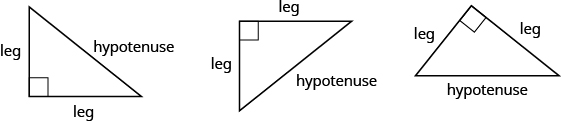
Remember that a right triangle has a [latex]90^\circ[/latex] angle, which we usually mark with a small square in the corner. The side of the triangle opposite the [latex]90^\circ[/latex] angle is called the hypotenuse, and the other two sides are called the legs. See the triangles below.

In a right triangle, the side opposite the [latex]90^\circ[/latex] angle is called the hypotenuse and each of the other sides is called a leg.

Three right triangles are shown. Each has a box representing the right angle. The first one has the right angle in the lower left corner, the next in the upper left corner, and the last one at the top. The two sides touching the right angle are labeled “leg” in each triangle. The sides across from the right angles are labeled “hypotenuse.”
The Pythagorean theorem tells how the lengths of the three sides of a right triangle relate to each other. It states that in any right triangle, the sum of the squares of the two legs equals the square of the hypotenuse.

The Pythagorean Theorem

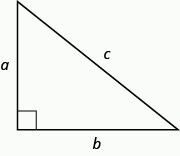
In any right triangle [latex]\Delta ABC[/latex],

[latex]{a}^{2}+{b}^{2}={c}^{2}[/latex]

where [latex]c[/latex] is the length of the hypotenuse [latex]a[/latex] and [latex]b[/latex] are the lengths of the legs.

A right triangle is shown. The right angle is marked with a box. Across from the box is side c. The sides touching the right angle are marked a and b.

To solve problems that use the Pythagorean theorem, we will need to find square roots. Previously, we introduced the notation [latex]\sqrt{m}[/latex] and defined it in this way:

[latex]\text{If }m={n}^{2},\text{ then }\sqrt{m}=n\text{ for }n\ge 0[/latex]

For example, we found that [latex]\sqrt{25}[/latex] is [latex]5[/latex] because [latex]{5}^{2}=25[/latex].

We will use this definition of square roots to solve for the length of a side in a right triangle.

example

Use the Pythagorean theorem to find the length of the hypotenuse.

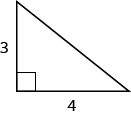
Right triangle with legs labeled as 3 and 4.

Solution

Step 1. Read the problem.
Step 2. Identify what you are looking for.	the length of the hypotenuse of the triangle
Step 3. Name. Choose a variable to represent it.	Let [latex]c=\text{the length of the hypotenuse}[/latex]
Step 4. Translate. Write the appropriate formula. Substitute.	[latex]{a}^{2}+{b}^{2}={c}^{2}[/latex] [latex]{3}^{2}+{4}^{2}={c}^{2}[/latex]
Step 5. Solve the equation.	[latex]9+16={c}^{2}[/latex] [latex]25={c}^{2}[/latex] [latex]\sqrt{25}={c}[/latex] [latex]5=c[/latex]
Step 6. Check:	[latex]{3}^{2}+{4}^{2}=\color{red}{{5}^{2}}[/latex] [latex]9+16\stackrel{?}{=}25[/latex] [latex]25+25\checkmark[/latex]
Step 7. Answer the question.	The length of the hypotenuse is [latex]5[/latex].

try it

example

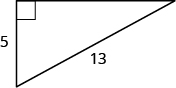
Use the Pythagorean theorem to find the length of the longer leg.

Right triangle is shown with one leg labeled as 5 and hypotenuse labeled as 13.

Show Solution

try it

example

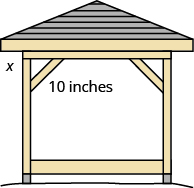
Kelvin is building a gazebo and wants to brace each corner by placing a [latex]\text{10-inch}[/latex] wooden bracket diagonally as shown. How far below the corner should he fasten the bracket if he wants the distances from the corner to each end of the bracket to be equal? Approximate to the nearest tenth of an inch.

A picture of a gazebo is shown. Beneath the roof is a rectangular shape. There are two braces from the top to each side. The brace on the left is labeled as 10 inches. From where the brace hits the side to the roof is labeled as x.

Show Solution

try it

In the following video we show two more examples of how to use the Pythagorean theorem to solve application problems.

Step 1. Read the problem.
Step 2. Identify what you are looking for.	The length of the leg of the triangle
Step 3. Name. Choose a variable to represent it.	Let [latex]b=\text{the leg of the triangle}[/latex] Label side b
Step 4. Translate. Write the appropriate formula. Substitute.	[latex]{a}^{2}+{b}^{2}={c}^{2}[/latex] [latex]{5}^{2}+{b}^{2}={13}^{2}[/latex]
Step 5. Solve the equation. Isolate the variable term. Use the definition of the square root. Simplify.	[latex]25+{b}^{2}=169[/latex] [latex]{b}^{2}=144[/latex] [latex]{b}=\sqrt{144}[/latex] [latex]b=12[/latex]
Step 6. Check: [latex]{5}^{2}+\color{red}{12}^{2}\stackrel{?}{=}{13}^{2}[/latex] [latex]25+144\stackrel{?}{=}169[/latex] [latex]169=169\checkmark[/latex]
Step 7. Answer the question.	The length of the leg is [latex]12[/latex].

Step 1. Read the problem.
Step 2. Identify what you are looking for.	the distance from the corner that the bracket should be attached
Step 3. Name. Choose a variable to represent it.	Let x = the distance from the corner
Step 4. Translate. Write the appropriate formula. Substitute.	[latex]{a}^{2}+{b}^{2}={c}^{2}[/latex] [latex]{x}^{2}+{x}^{2}={10}^{2}[/latex]
Step 5. Solve the equation. Isolate the variable. Use the definition of the square root. Simplify. Approximate to the nearest tenth.	[latex]2x^2=100[/latex] [latex]x^2=50[/latex] [latex]x=\sqrt{50}[/latex] [latex]b\approx{7.1}[/latex]
Step 6. Check: [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex] [latex](\color{red}{7.1})^2+(\color{red}{7.1})^{2}\stackrel{\text{?}}{\approx}{10}^{2}[/latex] [latex]50.41+50.41=100.82\approx{100}\quad\checkmark[/latex] Yes.
Step 7. Answer the question.	Kelvin should fasten each piece of wood approximately [latex]7.1in[/latex] from the corner.

Module 8: Geometry