Learning Outcomes
- Use properties of triangles
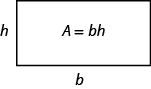
We now know how to find the area of a rectangle. We can use this fact to help us visualize the formula for the area of a triangle. In the rectangle below, we’ve labeled the length [latex]b[/latex] and the width [latex]h[/latex], so it’s area is [latex]bh[/latex].
The area of a rectangle is the base, [latex]b[/latex], times the height, [latex]h[/latex].
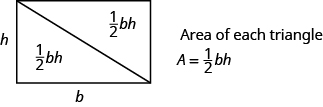
We can divide this rectangle into two congruent triangles (see the image below). Triangles that are congruent have identical side lengths and angles, and so their areas are equal. The area of each triangle is one-half the area of the rectangle, or [latex]\Large\frac{1}{2}\normalsize bh[/latex]. This example helps us see why the formula for the area of a triangle is [latex]A=\Large\frac{1}{2}\normalsize bh[/latex].
A rectangle can be divided into two triangles of equal area. The area of each triangle is one-half the area of the rectangle.
The formula for the area of a triangle is [latex]A=\Large\frac{1}{2}\normalsize bh[/latex], where [latex]b[/latex] is the base and [latex]h[/latex] is the height.
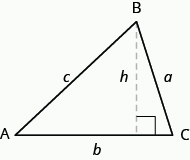
To find the area of the triangle, you need to know its base and height. The base is the length of one side of the triangle, usually the side at the bottom. The height is the length of the line that connects the base to the opposite vertex, and makes a [latex]\text{90}^ \circ[/latex] angle with the base. The image below shows three triangles with the base and height of each marked.
The height [latex]h[/latex] of a triangle is the length of a line segment that connects the the base to the opposite vertex and makes a [latex]\text{90}^ \circ[/latex] angle with the base.

Triangle Properties
For any triangle [latex]\Delta ABC[/latex], the sum of the measures of the angles is [latex]\text{180}^ \circ[/latex].
[latex]m\angle{A}+m\angle{B}+m\angle{C}=180^\circ[/latex]
The perimeter of a triangle is the sum of the lengths of the sides.
[latex]P=a+b+c[/latex]
The area of a triangle is one-half the base, [latex]b[/latex], times the height, [latex]h[/latex].
[latex]A={\Large\frac{1}{2}}bh[/latex]
example
Find the area of a triangle whose base is [latex]11[/latex] inches and whose height is [latex]8[/latex] inches.
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. |  |
| Step 2. Identify what you are looking for. | the area of the triangle |
| Step 3. Name. Choose a variable to represent it. | let A = area of the triangle |
| Step 4.Translate.
Write the appropriate formula. Substitute. |
 |
| Step 5. Solve the equation. | [latex]A=44[/latex] square inches. |
| Step 6. Check:
[latex]A={ \Large\frac{1}{2}}bh[/latex] [latex]44\stackrel{?}{=}{ \Large\frac{1}{2}}(11)8[/latex] [latex]44=44\quad\checkmark[/latex] |
|
| Step 7. Answer the question. | The area is [latex]44[/latex] square inches. |
try it
The following video provides another example of how to use the area formula for triangles.
example
The perimeter of a triangular garden is [latex]24[/latex] feet. The lengths of two sides are [latex]4[/latex] feet and [latex]9[/latex] feet. How long is the third side?
try it
example
The area of a triangular church window is [latex]90[/latex] square meters. The base of the window is [latex]15[/latex] meters. What is the window’s height?
try it
In our next video, we show another example of how to find the height of a triangle given it’s area.
Isosceles and Equilateral Triangles
Besides the right triangle, some other triangles have special names. A triangle with two sides of equal length is called an isosceles triangle. A triangle that has three sides of equal length is called an equilateral triangle. The image below shows both types of triangles.
In an isosceles triangle, two sides have the same length, and the third side is the base. In an equilateral triangle, all three sides have the same length.
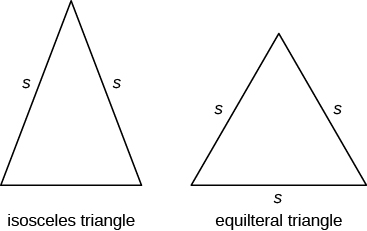
Isosceles and Equilateral Triangles
An isosceles triangle has two sides the same length.
An equilateral triangle has three sides of equal length.
example
The perimeter of an equilateral triangle is [latex]93[/latex] inches. Find the length of each side.
try it
example
Arianna has [latex]156[/latex] inches of beading to use as trim around a scarf. The scarf will be an isosceles triangle with a base of [latex]60[/latex] inches. How long can she make the two equal sides?
try it
Candela Citations
- Question ID 146531, 146528, 146526, 146525. Authored by: Lumen Learning. License: CC BY: Attribution
- Ex: Find the Area of a Triangle (Whole Number). Authored by: James Sousa (mathispower4u.com). Located at: https://youtu.be/jXbPAk2jorM. License: CC BY: Attribution
- Ex: Find the Height of a Triangle Given Area (Even Base). Authored by: James Sousa (mathispower4u.com). Located at: https://youtu.be/C0vUVK_o5r0. License: CC BY: Attribution
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@9.757









