The most common root is the square root. First, we will define what square roots are and how you find the square root of a number. Then we will apply similar ideas to define and evaluate nth roots.

Roots are the inverse of exponents, much like multiplication is the inverse of division. Recall that exponents are defined and written as repeated multiplication.

Exponent: [latex]{{3}^{2}}[/latex], [latex]{{4}^{5}}[/latex], [latex]{{x}^{3}}[/latex], [latex]{{x}^{\text{n}}}[/latex]

Name: “Three squared” or “Three to the second power”, “Four to the fifth power”, “x cubed”, “x to the nth power”

Repeated Multiplication: [latex]3\cdot 3[/latex],  [latex]4\cdot 4\cdot 4\cdot 4\cdot 4[/latex],  [latex]x\cdot x\cdot x[/latex],  [latex]\underbrace{x\cdot x\cdot x...\cdot x}_{n\text{ times}}[/latex].

Conversely,  when you are trying to find the square root of a number (say, [latex]25[/latex]), you are trying to find a number that can be multiplied by itself to create that original number. In the case of [latex]25[/latex], you find that [latex]5\cdot5=25[/latex], so [latex]5[/latex] must be the square root.

Find the square roots of the following numbers:

1. [latex]36[/latex]
2. [latex]81[/latex]
3. [latex]-49[/latex]
4. [latex]0[/latex]

 

1. We want to find a number whose square is [latex]36[/latex]. [latex]6^2=36[/latex] therefore,  the nonnegative square root of [latex]36[/latex] is [latex]6[/latex] and the negative square root of [latex]36[/latex] is [latex]-6[/latex]
2. We want to find a number whose square is [latex]81[/latex]. [latex]9^2=81[/latex] therefore,  the nonnegative square root of [latex]81[/latex] is [latex]9[/latex] and the negative square root of [latex]81[/latex] is [latex]-9[/latex]
3. We want to find a number whose square is [latex]-49[/latex]. When you square a real number, the result is always positive. Stop and think about that for a second. A negative number times itself is positive, and a positive number times itself is positive.  Therefore, [latex]-49[/latex] does not have square roots, there are no real number solutions to this question.
4. We want to find a number whose square is [latex]0[/latex]. [latex]0^2=0[/latex] therefore,  the nonnegative square root of [latex]0[/latex] is [latex]0[/latex].  We do not assign [latex]0[/latex] a sign, so it has only one square root, and that is [latex]0[/latex].

The symbol for the square root is called a radical symbol and looks like this: [latex]\sqrt{\,\,\,}[/latex]. The expression [latex]\sqrt{25}[/latex] is read “the square root of twenty-five” or “radical twenty-five.” The number that is written under the radical symbol is called the radicand.

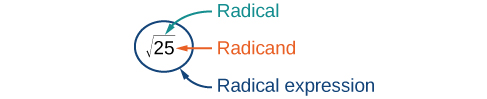
The notation that we use to express a square root for any real number, a, is as follows:

Consider [latex]\sqrt{25}[/latex] again. You may realize that there is another value that, when multiplied by itself, also results in [latex]25[/latex]. That number is [latex]−5[/latex].

[latex]\begin{array}{r}5\cdot 5=25\\-5\cdot -5=25\end{array}[/latex]

By definition, the square root symbol always means to find the positive root called the principal root. So while [latex]5\cdot5[/latex] and [latex]−5\cdot−5[/latex] both equal [latex]25[/latex], only [latex]5[/latex] is the principal root. You should also know that zero is special because it has only one square root: itself (since [latex]0\cdot0=0[/latex]).

Let’s do an example similar to the example from above, this time using square root notation.  Note that using the square root notation means that you are only finding the principal root – the nonnegative root.

The last problem in the previous example shows us an important relationship between squares and square roots, and we can summarize it as follows:

The following table shows different radicals and their equivalent written and simplified forms.

Radical	Name	Simplified Form
[latex]\sqrt{36}[/latex]	“Square root of thirty-six” “Radical thirty-six”	[latex]\sqrt{36}=\sqrt{6^2}=6[/latex]
[latex]\sqrt{100}[/latex]	“Square root of one hundred” “Radical one hundred”	[latex]\sqrt{100}=\sqrt{10^2}=10[/latex]
[latex]\sqrt{225}[/latex]	“Square root of two hundred twenty-five” “Radical two hundred twenty-five”	[latex]\sqrt{225}=\sqrt{15^2}=15[/latex]

In the video that follows, we simplify more square roots using the fact that  [latex]\sqrt{a^2}=a[/latex] means finding the principal square root.

Finding Square Roots Using Factoring

What if you are working with a number whose square you do not know right away?  We can use factoring and the product rule for square roots to find square roots such as [latex]\sqrt{144}[/latex], or  [latex]\sqrt{225}[/latex].

In the examples that follow we will bring together these ideas to simplify square roots of numbers that are not obvious at first glance:

• square root of a square,
• the product rule for square roots
• factoring

 

 

Let’s look at some more examples of expressions with square roots.  Pay particular attention to how number 3 is evaluated.

In the following video, we present more examples of how to find a principal square root.

The last example we showed leads reminds us of an important characteristic of square roots. You can only take the square root of values that are non-negative.

So far, you have seen examples that are perfect squares. That is, each is a number whose square root is an integer. But many radical expressions are not perfect squares. Some of these radicals can still be simplified by finding perfect square factors. The example below illustrates how to factor the radicand, looking for pairs of factors that can be expressed as a square.

The final answer [latex]3\sqrt{7}[/latex] may look a bit odd, but it is in simplified form. You can read this as “three radical seven” or “three times the square root of seven.”

In the next example, we take a bit of a shortcut by making use of the common squares we know, instead of using prime factors. It helps to have the squares of the numbers between [latex]0[/latex] and [latex]10[/latex] fresh in your mind to make simplifying radicals faster.

• [latex]0^2=0[/latex]
• [latex]2^2=4[/latex]
• [latex]3^2=9[/latex]
• [latex]4^2=16[/latex]
• [latex]5^2=25[/latex]
• [latex]6^2=36[/latex]
• [latex]7^2=49[/latex]
• [latex]8^2=64[/latex]
• [latex]9^2=81[/latex]
• [latex]10^2=100[/latex]

In this last video, we show examples of simplifying radicals that are not perfect squares.

 

Estimate Roots

An approach to handling roots that are not perfect squares is to approximate them by comparing the values to perfect squares. Suppose you wanted to know the square root of [latex]17[/latex]. Let us look at how you might approximate it.

This approximation is pretty close. If you kept using this trial and error strategy, then you could continue to find the square root to the thousandths, ten-thousandths, and hundred-thousandths places, but eventually it would become too tedious to do by hand.

For this reason, when you need to find a more precise approximation of a square root, you should use a calculator. Most calculators have a square root key [latex](\sqrt{{}})[/latex] that will give you the square root approximation quickly. On a simple [latex]4[/latex]-function calculator, you would likely key in the number that you want to take the square root of and then press the square root key.

Try to find [latex]\sqrt{17}[/latex] using your calculator. Note that you will not be able to get an “exact” answer because [latex]\sqrt{17}[/latex] is an irrational number, a number that cannot be expressed as a fraction, and the decimal never terminates or repeats. To nine decimal positions, [latex]\sqrt{17}[/latex] is approximated as [latex]4.123105626[/latex]. A calculator can save a lot of time and yield a more precise square root when you are dealing with numbers that are not perfect squares.

The following video shows another example of how to estimate a square root.

Summary

The square root of a number is the number which, when multiplied by itself, gives the original number. Principal square roots are always positive and the square root of [latex]0[/latex] is [latex]0[/latex]. You can only take the square root of values that are nonnegative. The square root of a perfect square will be an integer. Other square roots can be simplified by identifying factors that are perfect squares and taking their square root.  Square roots that are not perfect can also be estimated by finding the perfect square above and below your number.  Also, using a calculator is useful for finding a more precise approximation of a square root.