Learning Outcomes
- Identify radicals that can be added or subtracted
- Add and subtract radical expressions
Adding and subtracting radicals is much like combining like terms with variables. We can add and subtract expressions with variables like this:
[latex]5x+3y - 4x+7y=x+10y[/latex]
There are two keys to combining radicals by addition or subtraction: look at the index, and look at the radicand. If these are the same, then addition and subtraction are possible. If not, then you cannot combine the two radicals.
Remember the index is the degree of the root and the radicand is the term or expression under the radical. In the diagram below, the index is n, and the radicand is [latex]100[/latex]. The radicand is placed under the root symbol and the index is placed outside the root symbol to the left:
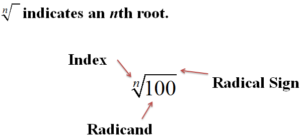
Index and radicand
In the graphic below, the index of the expression [latex]12\sqrt[3]{xy}[/latex] is [latex]3[/latex] and the radicand is [latex]xy[/latex].
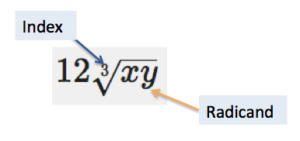
Practice identifying radicals that are compatible for addition and subtraction by looking at the index and radicand of the roots in the following example.
Example
Identify the roots that have the same index and radicand.
[latex] 10\sqrt{6}[/latex]
[latex] -1\sqrt[3]{6}[/latex]
[latex] \sqrt{25}[/latex]
[latex] 12\sqrt{6}[/latex]
[latex] \frac{1}{2}\sqrt[3]{25}[/latex]
[latex] -7\sqrt[3]{6}[/latex]
Making sense of a string of radicals may be difficult. One helpful tip is to think of radicals as variables, and treat them the same way. When you add and subtract variables, you look for like terms, which is the same thing you will do when you add and subtract radicals.
Let’s use this concept to add some radicals.
In this first example, both radicals have the same radicand and index.
Example
Add. [latex] 3\sqrt{11}+7\sqrt{11}[/latex]
It may help to think of radical terms with words when you are adding and subtracting them. The last example could be read “three square roots of eleven plus [latex]7[/latex] square roots of eleven”.
This next example contains more addends, or terms that are being added together. Notice how you can combine like terms (radicals that have the same root and index) but you cannot combine unlike terms.
Example
Add. [latex] 5\sqrt{2}+\sqrt{3}+4\sqrt{3}+2\sqrt{2}[/latex]
Notice that the expression in the previous example is simplified even though it has two terms: [latex] 7\sqrt{2}[/latex] and [latex] 5\sqrt{3}[/latex]. It would be a mistake to try to combine them further! (Some people make the mistake that [latex] 7\sqrt{2}+5\sqrt{3}=12\sqrt{5}[/latex]. This is incorrect because[latex] \sqrt{2}[/latex] and [latex]\sqrt{3}[/latex] are not like radicals so they cannot be added.)
Example
Add. [latex] 3\sqrt{x}+12\sqrt[3]{xy}+\sqrt{x}[/latex]
In the following video, we show more examples of how to identify and add like radicals.
Try It
Sometimes you may need to add and simplify the radical. If the radicals are different, try simplifying first—you may end up being able to combine the radicals at the end, as shown in these next two examples.
Example
Add and simplify. [latex] 2\sqrt[3]{40}+\sqrt[3]{135}[/latex]
Example
Add and simplify. [latex] x\sqrt[3]{x{{y}^{4}}}+y\sqrt[3]{{{x}^{4}}y}[/latex]
The following video shows more examples of adding radicals that require simplification.
Subtracting Radicals
Subtraction of radicals follows the same set of rules and approaches as addition—the radicands and the indices (plural of index) must be the same for two (or more) radicals to be subtracted. In the examples that follow, subtraction has been rewritten as addition of the opposite.
Example
Subtract. [latex] 5\sqrt{13}-3\sqrt{13}[/latex]
Example
Subtract. [latex] 4\sqrt[3]{5a}-\sqrt[3]{3a}-2\sqrt[3]{5a}[/latex]
In the video examples that follow, we show more examples of how to add and subtract radicals that don’t need to be simplified beforehand.
Example
Subtract and simplify. [latex] 5\sqrt[4]{{{a}^{5}}b}-a\sqrt[4]{16ab}[/latex], where [latex]a\ge 0[/latex] and [latex]b\ge 0[/latex]
In our last videos, we show more examples of subtracting radicals that require simplifying.
Summary
Combining radicals is possible when the index and the radicand of two or more radicals are the same. Radicals with the same index and radicand are known as like radicals. It is often helpful to treat radicals just as you would treat variables: like radicals can be added and subtracted in the same way that like variables can be added and subtracted. Sometimes, you will need to simplify a radical expression before it is possible to add or subtract like terms.
