Classifying Polynomials

Learning Outcomes

  • Identify polynomials, monomials, binomials, and trinomials
  • Determine the degree of polynomials

Polynomials come in many forms. They can vary by how many terms, or monomials, make up the polynomial and they also can vary by the degrees of the monomials in the polynomial. In this section, we will look at different ways that we classify polynomials. First, we will classify polynomials by the number of terms in the polynomial and then we will classify them by the monomial with the largest exponent.

Identify Polynomials, Monomials, Binomials, and Trinomials

A monomial, or a sum and/or difference of monomials, is called a polynomial.  A polynomial containing two terms, such as [latex]2x - 9[/latex], is called a binomial.  A polynomial containing three terms, such as [latex]-3{x}^{2}+8x - 7[/latex], is called a trinomial.

Polynomials

polynomial—A monomial, or two or more monomials, combined by addition or subtraction (“poly” means many)
monomial—A polynomial with exactly one term (“mono” means one)
binomial— A polynomial with exactly two terms (“bi” means two)
trinomial—A polynomial with exactly three terms (“tri” means three)

Here are some examples of polynomials:

Polynomial [latex]b+1[/latex] [latex]4{y}^{2}-7y+2[/latex] [latex]5{x}^{5}-4{x}^{4}+{x}^{3}+8{x}^{2}-9x+1[/latex]
Monomial [latex]5[/latex] [latex]4{b}^{2}[/latex] [latex]-9{x}^{3}[/latex]
Binomial [latex]3a - 7[/latex] [latex]{y}^{2}-9[/latex] [latex]17{x}^{3}+14{x}^{2}[/latex]
Trinomial [latex]{x}^{2}-5x+6[/latex] [latex]4{y}^{2}-7y+2[/latex] [latex]5{a}^{4}-3{a}^{3}+a[/latex]

Notice that every monomial, binomial, and trinomial is also a polynomial. They are special members of the family of polynomials and so they have special names. We use the words ‘monomial’, ‘binomial’, and ‘trinomial’ when referring to these special polynomials and just call all the rest ‘polynomials’.

example

Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial:

1. [latex]8{x}^{2}-7x - 9[/latex]
2. [latex]-5{a}^{4}[/latex]
3. [latex]{x}^{4}-7{x}^{3}-6{x}^{2}+5x+2[/latex]
4. [latex]11 - 4{y}^{3}[/latex]
5. [latex]n[/latex]

Solution

Polynomial Number of terms Type
1. [latex]8{x}^{2}-7x - 9[/latex] [latex]3[/latex] Trinomial
2. [latex]-5{a}^{4}[/latex] [latex]1[/latex] Monomial
3. [latex]{x}^{4}-7{x}^{3}-6{x}^{2}+5x+2[/latex] [latex]5[/latex] Polynomial
4. [latex]11 - 4{y}^{3}[/latex] [latex]2[/latex] Binomial
5. [latex]n[/latex] [latex]1[/latex] Monomial

Example

For the following expressions, determine whether they are a polynomial. If so, categorize them as a monomial, binomial, or trinomial.

  1. [latex]\frac{x-3}{1-x}+x^2[/latex]
  2. [latex]t^2+2t-3[/latex]
  3. [latex]x^3+\frac{x}{8}[/latex]
  4. [latex]\frac{\sqrt{y}}{2}-y-1[/latex]

try it

In the following video, you will be shown more examples of how to identify and categorize polynomials.

Determining the Degree of Polynomials

We can find the degree of a polynomial by identifying the highest power of the variable that occurs in the polynomial. Polynomials can be classified by the degree of the polynomial. The degree of a polynomial is the degree of its highest degree term. So the degree of [latex]2x^{3}+3x^{2}+8x+5[/latex] is 3.

A polynomial is said to be written in standard form when the terms are arranged from the highest degree to the lowest degree. When it is written in standard form it is easy to determine the degree of the polynomial.  The term with the highest degree is called the leading term because it is written first in standard form. The coefficient of the leading term is called the leading coefficient.

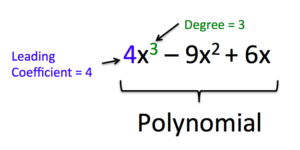
4x^3 - 9x^2 + 6x, with the text "degree = 3" and an arrow pointing at the exponent on x^3, and the text "leading term =4" with an arrow pointing at the 4.

How to: Given a polynomial expression, identify the degree and leading coefficient

  1. Find the highest power of the variable (usually x) to determine the degree.
  2. Identify the term containing the highest power of the variable to find the leading term.
  3. Identify the coefficient of the leading term.

Degree of a Polynomial

The degree of a term is the exponent of its variable.
The degree of a constant is [latex]0[/latex].
The degree of a polynomial is the highest degree of all its terms.

When the coefficient of a polynomial term is [latex]0[/latex], you usually do not write the term at all (because [latex]0[/latex] times anything is [latex]0[/latex], and adding [latex]0[/latex] does not change the value).

A term without a variable is called a constant term, and the degree of that term is [latex]0[/latex].  In the polynomial [latex]3x+13[/latex], we could have written the polynomial as [latex]3x^{1}+13x^{0}[/latex].  Although this is not how we would normally write this, it allows us to see that [latex]13[/latex] is the constant term because its degree is 0 and the degree of [latex]3x[/latex] is 1.  The degree of this binomial is 1.

If a polynomial does not have a constant term, like in the polynomial [latex]14x^{3}+3x[/latex] we would say that the constant term is [latex]0[/latex].

Let’s see how this works by looking at several polynomials. We’ll take it step by step, starting with monomials, and then progressing to polynomials with more terms.

Remember: Any base written without an exponent has an implied exponent of [latex]1[/latex].

This table has 11 rows and 5 columns. The first column is a header column, and it names each row. The first row is named “Monomial,” and each cell in this row contains a different monomial. The second row is named “Degree,” and each cell in this row contains the degree of the monomial above it. The degree of 14 is 0, the degree of 8y squared is 2, the degree of negative 9x cubed y to the fifth power is 8, and the degree of negative 13a is 1. The third row is named “Binomial,” and each cell in this row contains a different binomial. The fourth row is named “Degree of each term,” and each cell contains the degrees of the two terms in the binomial above it. The fifth row is named “Degree of polynomial,” and each cell contains the degree of the binomial as a whole.” The degrees of the terms in a plus 7 are 0 and 1, and the degree of the whole binomial is 1. The degrees of the terms in 4b squared minus 5b are 2 and 1, and the degree of the whole binomial is 2. The degrees of the terms in x squared y squared minus 16 are 4 and 0, and the degree of the whole binomial is 4. The degrees of the terms in 3n cubed minus 9n squared are 3 and 2, and the degree of the whole binomial is 3. The sixth row is named “Trinomial,” and each cell in this row contains a different trinomial. The seventh row is named “Degree of each term,” and each cell contains the degrees of the three terms in the trinomial above it. The eighth row is named “Degree of polynomial,” and each cell contains the degree of the trinomial as a whole. The degrees of the terms in x squared minus 7x plus 12 are 2, 1, and 0, and the degree of the whole trinomial is 2. The degrees of the terms in 9a squared plus 6ab plus b squared are 2, 2, and 2, and the degree of the trinomial as a whole is 2. The degrees of the terms in 6m to the fourth power minus m cubed n squared plus 8mn to the fifth power are 4, 5, and 6, and the degree of the whole trinomial is 6. The degrees of the terms in z to the fourth power plus 3z squared minus 1 are 4, 2, and 0, and the degree of the whole trinomial is 4. The ninth row is named “Polynomial,” and each cell contains a different polynomial. The tenth row is named “Degree of each term,” and the eleventh row is named “Degree of polynomial.” The degrees of the terms in b plus 1 are 1 and 0, and the degree of the whole polynomial is 1. The degrees of the terms in 4y squared minus 7y plus 2 are 2, 1, and 0, and the degree of the whole polynomial is 2. The degrees of the terms in 4x to the fourth power plus x cubed plus 8x squared minus 9x plus 1 are 4, 3, 2, 1, and 0, and the degree of the whole polynomial is 4.

 

example

Find the degree of the following polynomials:

1. [latex]4x[/latex]
2. [latex]3{x}^{3}-5x+7[/latex]
3. [latex]-11[/latex]
4. [latex]-6{x}^{2}+9x - 3[/latex]
5. [latex]8x+2[/latex]

Working with polynomials is easier when you list the terms in descending order of degrees. When a polynomial is written this way, it is said to be in standard form. Look back at the polynomials in the previous example. Notice that they are all written in standard form. Get in the habit of writing the term with the highest degree first.

try it

Example

For the following polynomials, identify the degree, the leading term, and the leading coefficient.

  1. [latex]3+2{x}^{2}-4{x}^{3}[/latex]
  2. [latex]5{t}^{5}-2{t}^{3}+7t[/latex]
  3. [latex]6p-{p}^{3}-2[/latex]

In the following video, we will identify the terms, leading coefficient, and degree of a polynomial.