Classifying Real Numbers

Learning Outcomes

  • Identify rational numbers and irrational numbers
  • Classify different types of real numbers

The real numbers can be divided into three subsets: negative real numbers, zero, and positive real numbers. Each subset includes fractions, decimals, and irrational numbers according to their algebraic sign (+ or –). In this section we will further define real numbers and use their properties to solve linear equations and inequalities.

To begin, we will review the natural numbers, whole numbers, and integers that have already been covered in this course.  We will then discuss the rational numbers and irrational numbers in greater detail.

Natural numbers

The most familiar numbers are the natural numbers (sometimes called counting numbers): [latex]1, 2, 3[/latex], and so on.  These are numbers we use for counting, or enumerating items.  The mathematical symbol for the set of all natural numbers is written as [latex]\mathbb{N}[/latex].  We describe them in set notation as [latex]\{1, 2, 3, ...\}[/latex] where the ellipsis (…) indicates that the numbers continue to infinity. The natural numbers are, of course, also called the counting numbers. Any time we enumerate the members of a team, count the coins in a collection, or tally the trees in a grove, we are using the set of natural numbers.

Whole numbers

The set of whole numbers includes all natural numbers as well as  [latex]0[/latex]:  [latex]\{0, 1, 2, 3,...\}[/latex].

Integers

When the set of negative numbers is combined with the set of natural numbers (including 0), the result is defined as the set of integers, [latex]\mathbb{Z}[/latex].  The set of integers adds the opposites of the natural numbers to the set of whole numbers: {…−3,−2,−1,0,1,2,3,…}{…−3,−2,−1,0,1,2,3,…}. It is useful to note that the set of integers is made up of three distinct subsets: negative integers, zero, and positive integers. In this sense, the positive integers are just the natural numbers. Another way to think about it is that the natural numbers are a subset of the integers.

[latex]\begin{array}{lll}{\text{negative integers}}\hfill & {\text{zero}}\hfill & {\text{positive integers}}\\{\dots ,-3,-2,-1,}\hfill & {0,}\hfill & {1,2,3,\dots }\end{array}[/latex]

Rational numbers

What type of numbers would you get if you started with all the integers and then included all the fractions? The numbers you would have form the set of rational numbers. A rational number is a number that can be written as a ratio of two integers.

Rational Numbers

A rational number is a number that can be written in the form [latex]{\Large\frac{p}{q}}[/latex], where [latex]p[/latex] and [latex]q[/latex] are integers and [latex]q\ne 0[/latex].

A rational number, [latex]\mathbb{Q}[/latex], is a number that can be expressed as a fraction with an integer numerator and a positive integer denominator.  The set of rational numbers is written as [latex]\left\{\dfrac{m}{n}\normalsize |m\text{ and }{n}\text{ are integers and }{n}\ne{ 0 }\right\}[/latex]. Notice from the definition that rational numbers are fractions (or quotients) containing integers in both the numerator and the denominator, and the denominator is never [latex]0[/latex]. We can also see that every natural number, whole number, and integer is a rational number with a denominator of [latex]1[/latex].

All fractions, both positive and negative, are rational numbers. A few examples are

[latex]\Large\frac{4}{5}\normalsize ,-\Large\frac{7}{8}\normalsize ,\Large\frac{13}{4}\normalsize ,\text{and}-\Large\frac{20}{3}[/latex]

Each numerator and each denominator is an integer.

We need to look at all the numbers we have used so far and verify that they are rational. The definition of rational numbers tells us that all fractions are rational. We will now look at the counting numbers, whole numbers, integers, and decimals to make sure they are rational.

Integers are rational

Are integers rational numbers? To decide if an integer is a rational number, we try to write it as a ratio of two integers. An easy way to do this is to write it as a fraction with denominator one.

[latex]3=\Large\frac{3}{1}\normalsize ,\space-8=\Large\frac{-8}{1}\normalsize ,\space0=\Large\frac{0}{1}[/latex]

Since any integer can be written as the ratio of two integers, all integers are rational numbers. Remember that all the counting numbers and all the whole numbers are also integers, and so they, too, are rational.

Decimals are rational

What about decimals? Are they rational? Let’s look at a few to see if we can write each of them as the ratio of two integers. We’ve already seen that integers are rational numbers. The integer [latex]-8[/latex] could be written as the decimal [latex]-8.0[/latex]. So, clearly, some decimals are rational.

Think about the decimal [latex]7.3[/latex]. Can we write it as a ratio of two integers? Because [latex]7.3[/latex] means [latex]7\Large\frac{3}{10}[/latex], we can write it as an improper fraction, [latex]\Large\frac{73}{10}[/latex]. So [latex]7.3[/latex] is the ratio of the integers [latex]73[/latex] and [latex]10[/latex]. It is a rational number.

In general, any decimal that ends after a number of digits such as [latex]7.3[/latex] or [latex]-1.2684[/latex] is a rational number. We can use the place value of the last digit as the denominator when writing the decimal as a fraction.

example

Write each as the ratio of two integers:

1. [latex]-15[/latex]

2. [latex]6.81[/latex]

3. [latex]-3\Large\frac{6}{7}[/latex]

Solution:

1.
[latex]-15[/latex]
Write the integer as a fraction with denominator 1. [latex]\Large\frac{-15}{1}[/latex]
2.
[latex]6.81[/latex]
Write the decimal as a mixed number. [latex]6\Large\frac{81}{100}[/latex]
Then convert it to an improper fraction. [latex]\Large\frac{681}{100}[/latex]
3.
[latex]-3\Large\frac{6}{7}[/latex]
Convert the mixed number to an improper fraction. [latex]-\Large\frac{27}{7}[/latex]

 

try it

Rational numbers as decimals

Let’s look at the decimal form of the numbers we know are rational. We have seen that every integer is a rational number, since [latex]a=\Large\frac{a}{1}[/latex] for any integer, [latex]a[/latex]. We can also change any integer to a decimal by adding a decimal point and a zero.

Integer [latex]-2,-1,0,1,2,3[/latex]

Decimal [latex]-2.0,-1.0,0.0,1.0,2.0,3.0[/latex]

These decimal numbers stop.

We have also seen that every fraction is a rational number. Look at the decimal form of the fractions we just considered.

Ratio of Integers [latex]\Large\frac{4}{5}\normalsize ,\Large\frac{7}{8}\normalsize ,\Large\frac{13}{4}\normalsize ,\Large\frac{20}{3}[/latex]

Decimal Forms [latex]0.8,-0.875,3.25,-6.666\ldots,-6.\overline{66}[/latex]

These decimals either stop or repeat.

What do these examples tell you? Every rational number can be written both as a ratio of integers and as a decimal that either stops or repeats. The table below shows the numbers we looked at expressed as a ratio of integers and as a decimal.

Rational Numbers
Fractions Integers
Number [latex]\Large\frac{4}{5}\normalsize ,-\Large\frac{7}{8}\normalsize ,\Large\frac{13}{4}\normalsize ,\Large\frac{-20}{3}[/latex] [latex]-2,-1,0,1,2,3[/latex]
Ratio of Integer [latex]\Large\frac{4}{5}\normalsize ,\Large\frac{-7}{8}\normalsize ,\Large\frac{13}{4}\normalsize ,\Large\frac{-20}{3}[/latex] [latex]\Large\frac{-2}{1}\normalsize ,\Large\frac{-1}{1}\normalsize ,\Large\frac{0}{1}\normalsize ,\Large\frac{1}{1}\normalsize ,\Large\frac{2}{1}\normalsize ,\Large\frac{3}{1}[/latex]
Decimal number [latex]0.8,-0.875,3.25,-6.\overline{6}[/latex] [latex]-2.0,-1.0,0.0,1.0,2.0,3.0[/latex]

 

Because they are fractions, any rational number can also be expressed in decimal form. Any rational number can be represented as either:

  1. a terminating decimal: [latex]\dfrac{15}{8}\normalsize =1.875[/latex], or
  2. a repeating decimal: [latex]\dfrac{4}{11}\normalsize =0.36363636\dots =0.\overline{36}[/latex]

We use a line drawn over the repeating block of numbers instead of writing the group multiple times.

 

Example

Write each of the following as a rational number.

  1. [latex]7[/latex]
  2. [latex]0[/latex]
  3. [latex]–8[/latex]

Example

Write each of the following rational numbers as either a terminating or repeating decimal.

  1. [latex]-\dfrac{5}{7}[/latex]
  2. [latex]\dfrac{15}{5}[/latex]
  3. [latex]\dfrac{13}{25}[/latex]

Irrational Numbers

Are there any decimals that do not stop or repeat? Yes.  At some point in the ancient past, someone discovered that not all numbers are rational numbers. A builder, for instance, may have found that the diagonal of a square with unit sides was not [latex]2[/latex] or even [latex]\dfrac{3}{2}[/latex], but was something else. Or a garment maker might have observed that the ratio of the circumference to the diameter of a roll of cloth was a little bit more than [latex]3[/latex], but still not a rational number.  The number [latex]\pi[/latex] (the Greek letter pi, pronounced ‘pie’), which is very important in describing circles, has a decimal form that does not stop or repeat ([latex]\pi =\text{3.141592654.......}[/latex]).  Such numbers are said to be irrational because they cannot be written as fractions. These numbers make up the set of irrational numbers. Irrational numbers cannot be expressed as a fraction of two integers. It is impossible to describe this set of numbers by a single rule except to say that a number is irrational if it is not rational. So we write this as {h | h is not a rational number}.

Similarly, the decimal representations of square roots of numbers that are not perfect squares never stop and never repeat. For example,

[latex]\sqrt{5}=\text{2.236067978.....}[/latex]

A decimal that does not stop and does not repeat cannot be written as the ratio of integers. We call this kind of number an irrational number.

Irrational Number

An irrational number is a number that cannot be written as the ratio of two integers. Its decimal form does not stop and does not repeat.

Let’s summarize a method we can use to determine whether a number is rational or irrational.
If the decimal form of a number

  • stops or repeats, the number is rational.
  • does not stop and does not repeat, the number is irrational.

example

Identify each of the following as rational or irrational:
1. [latex]0.58\overline{3}[/latex]
2. [latex]0.475[/latex]
3. [latex]3.605551275\dots[/latex]

 

try it

 

Let’s think about square roots now. Square roots of perfect squares are always whole numbers, so they are rational. But the decimal forms of square roots of numbers that are not perfect squares never stop and never repeat, so these square roots are irrational.

example

Identify each of the following as rational or irrational:
1. [latex]\sqrt{36}[/latex]
2. [latex]\sqrt{44}[/latex]

 

try it

In the following video we show more examples of how to determine whether a number is irrational or rational.

Example

Determine whether each of the following numbers is rational or irrational. If it is rational, determine whether it is a terminating or repeating decimal.

  1. [latex]\sqrt{25}[/latex]
  2. [latex]\dfrac{33}{9}[/latex]
  3. [latex]\sqrt{11}[/latex]
  4. [latex]\dfrac{17}{34}[/latex]
  5. [latex]0.3033033303333\dots[/latex]

Real numbers

Given any number n, we know that n is either rational or irrational. It cannot be both. The sets of rational and irrational numbers together make up the set of real numbers.

Real Numbers

Real numbers are numbers that are either rational or irrational.

The real numbers include all the measuring numbers. The symbol for the real numbers is [latex]\mathbb{R}[/latex]. Real numbers are usually represented by using decimal numerals.  As we saw with integers, the real numbers can be divided into three subsets: negative real numbers, zero, and positive real numbers. Each subset includes fractions, decimals, and irrational numbers according to their algebraic sign (+ or –). Zero is considered neither positive nor negative.

The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as [latex]0[/latex], with negative numbers to the left of [latex]0[/latex] and positive numbers to the right of [latex]0[/latex]. A fixed unit distance is then used to mark off each integer (or other basic value) on either side of [latex]0[/latex]. Any real number corresponds to a unique position on the number line.  The converse is also true: Each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line as shown below.

A number line that is marked incrementing by 1 from negative five to five

The real number line.

 

Example

Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?

  1. [latex]-\dfrac{10}{3}[/latex]
  2. [latex]\sqrt{5}[/latex]
  3. [latex]-\sqrt{289}[/latex]
  4. [latex]-6\pi[/latex]
  5. [latex]0.615384615384\dots[/latex]

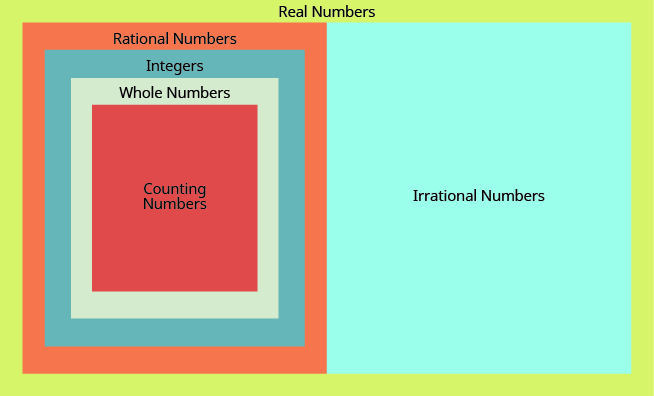
We have seen that all counting numbers are whole numbers, all whole numbers are integers, and all integers are rational numbers. Irrational numbers are a separate category of their own. When we put together the rational numbers and the irrational numbers, we get the set of real numbers.  Beginning with the natural numbers, we have expanded each set to form a larger set, meaning that there is a subset relationship between the sets of numbers we have encountered so far. These relationships become more obvious when seen as a diagram.

This diagram illustrates the relationships between the different types of real numbers.

The image shows a large rectangle labeled “Real Numbers”. The rectangle is split in half vertically. The right half is labeled “Irrational Numbers”. The left half is labeled “Rational Numbers” and contains three concentric rectangles. The outer most rectangle is labeled “Integers”, the next rectangle is “Whole Numbers” and the inner most rectangle is “Natural Numbers”.

Here is another visualization of the subsets of the real numbers.

A large box labeled: Real Numbers encloses five circles. Four of these circles enclose each other and the other is separate from the rest. The innermost circle contains: 1, 2, 3… N. The circle enclosing that circle contains: 0 W. The circle enclosing that circle contains: …, -3, -2, -1 I. The outermost circle contains: m/n, n not equal to zero Q. The separate circle contains: pi, square root of two, etc Q´.

Sets of numbers.   N: the set of natural numbers   W: the set of whole numbers   I: the set of integers   Q: the set of rational numbers   Q´: the set of irrational numbers

A General Note: Sets of Numbers

The set of natural numbers includes the numbers used for counting: [latex]\{1,2,3,\dots\}[/latex].

The set of whole numbers is the set of natural numbers and zero: [latex]\{0,1,2,3,\dots\}[/latex].

The set of integers adds the negative natural numbers to the set of whole numbers: [latex]\{\dots,-3,-2,-1,0,1,2,3,\dots\}[/latex].

The set of rational numbers includes fractions written as [latex]\{\dfrac{m}{n}\normalsize |m\text{ and }n\text{ are integers and }n\ne 0\}[/latex].

The set of irrational numbers is the set of numbers that are not rational. They are nonrepeating and nonterminating decimals: [latex]\{h|h\text{ is not a rational number}\}[/latex].

Does the term “real numbers” seem strange to you? Are there any numbers that are not “real”, and, if so, what could they be? For centuries, the only numbers people knew about were what we now call the real numbers. Then mathematicians discovered the set of imaginary numbers. You won’t encounter imaginary numbers in this module, but you will later on in your studies of algebra.

example

Determine whether each of the numbers in the following list is a 1. whole number, 2. integer, 3. rational number, 4. irrational number, and 5. real number.

[latex]-7,\Large\frac{14}{5}\normalsize ,8,\sqrt{5},5.9,-\sqrt{64}[/latex]

Solution:
1. The whole numbers are [latex]0,1,2,3\dots[/latex] The number [latex]8[/latex] is the only whole number given.

2. The integers are the whole numbers, their opposites, and [latex]0[/latex]. From the given numbers, [latex]-7[/latex] and [latex]8[/latex] are integers. Also, notice that [latex]64[/latex] is the square of [latex]8[/latex] so [latex]-\sqrt{64}=-8[/latex]. So the integers are [latex]-7,8,-\sqrt{64}[/latex].

3. Since all integers are rational, the numbers [latex]-7,8,\text{and}-\sqrt{64}[/latex] are also rational. Rational numbers also include fractions and decimals that terminate or repeat, so [latex]\Large\frac{14}{5}\normalsize\text{and}5.9[/latex] are rational.

4. The number [latex]5[/latex] is not a perfect square, so [latex]\sqrt{5}[/latex] is irrational.

5. All of the numbers listed are real.

We’ll summarize the results in a table.

Number Whole Integer Rational Irrational Real
[latex]-7[/latex] [latex]\quad\checkmark[/latex] [latex]\quad\checkmark[/latex] [latex]\quad\checkmark[/latex]
[latex]\Large\frac{14}{5}[/latex] [latex]\quad\checkmark[/latex] [latex]\quad\checkmark[/latex]
[latex]8[/latex] [latex]\quad\checkmark[/latex] [latex]\quad\checkmark[/latex] [latex]\quad\checkmark[/latex] [latex]\quad\checkmark[/latex]
[latex]\sqrt{5}[/latex] [latex]\quad\checkmark[/latex] [latex]\quad\checkmark[/latex]
[latex]5.9[/latex] [latex]\quad\checkmark[/latex] [latex]\quad\checkmark[/latex]
[latex]-\sqrt{64}[/latex] [latex]\quad\checkmark[/latex] [latex]\quad\checkmark[/latex] [latex]\quad\checkmark[/latex]

Example

Classify each number as being a natural number (N), whole number (W), integer (I), rational number (Q), and/or irrational number (Q’).

  1. [latex]\sqrt{36}[/latex]
  2. [latex]\dfrac{8}{3}[/latex]
  3. [latex]\sqrt{73}[/latex]
  4. [latex]-6[/latex]
  5. [latex]3.2121121112\dots[/latex]

 

try it

The following mini-lesson provides more examples of how to classify real numbers.