Learning Outcomes
- Divide decimals
Just as with multiplication, division of decimals is very much like dividing whole numbers. We just have to figure out where the decimal point must be placed.
To understand decimal division, let’s consider the multiplication problem
[latex]\left(0.2\right)\left(4\right)=0.8[/latex]
Remember, a multiplication problem can be rephrased as a division problem. So we can write
[latex]0.8\div 4=0.2[/latex]
We can think of this as “If we divide 8 tenths into four groups, how many are in each group?” The number line below shows that there are four groups of two-tenths in eight-tenths. So [latex]0.8\div 4=0.2[/latex].

Using long division notation, we would write
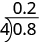
Notice that the decimal point in the quotient is directly above the decimal point in the dividend.
To divide a decimal by a whole number, we place the decimal point in the quotient above the decimal point in the dividend and then divide as usual. Sometimes we need to use extra zeros at the end of the dividend to keep dividing until there is no remainder.
Divide a decimal by a whole number.
- Write as long division, placing the decimal point in the quotient above the decimal point in the dividend.
- Divide as usual.
For a review on how to use the long division algorithm to divide multiple-digit numbers, click here.
example
Divide: [latex]0.12\div 3[/latex]
Solution
| [latex]0.12\div 3[/latex] | |
| Write as long division, placing the decimal point in the quotient above the decimal point in the dividend. | |
| Divide as usual. Since [latex]3[/latex] does not go into [latex]0[/latex] or [latex]1[/latex] we use zeros as placeholders. |  |
| [latex]0.12\div 3=0.04[/latex] |
try it
Watch the following video to see another example of how to divide a decimal by a whole number.
example
In everyday life, we divide whole numbers into decimals—money—to find the price of one item. For example, suppose a case of [latex]24[/latex] water bottles cost [latex]$3.99[/latex]. To find the price per water bottle, we would divide [latex]$3.99[/latex] by [latex]24[/latex], and round the answer to the nearest cent (hundredth).
Divide: [latex]$3.99\div 24[/latex]
try it
Divide a Decimal by Another Decimal
So far, we have divided a decimal by a whole number. What happens when we divide a decimal by another decimal? Let’s look at the same multiplication problem we looked at earlier, but in a different way.
[latex]\left(0.2\right)\left(4\right)=0.8[/latex]
Remember, again, that a multiplication problem can be rephrased as a division problem. This time we ask, “How many times does [latex]0.2[/latex] go into [latex]0.8\text{?"}[/latex] Because [latex]\left(0.2\right)\left(4\right)=0.8[/latex], we can say that [latex]0.2[/latex] goes into [latex]0.8[/latex] four times. This means that [latex]0.8[/latex] divided by [latex]0.2[/latex] is [latex]4[/latex].
[latex]0.8\div 0.2=4[/latex]

We would get the same answer, [latex]4[/latex], if we divide [latex]8[/latex] by [latex]2[/latex], both whole numbers. Why is this so? Let’s think about the division problem as a fraction.
[latex]\begin{array}{c}{\Large\frac{0.8}{0.2}}\\ \\ {\Large\frac{\left(0.8\right)10}{\left(0.2\right)10}}\\ \\ {\Large\frac{8}{2}}\\ \\ 4\end{array}[/latex]
We multiplied the numerator and denominator by [latex]10[/latex] and ended up just dividing [latex]8[/latex] by [latex]4[/latex]. To divide decimals, we multiply both the numerator and denominator by the same power of [latex]10[/latex] to make the denominator a whole number. Because of the Equivalent Fractions Property, we haven’t changed the value of the fraction. The effect is to move the decimal points in the numerator and denominator the same number of places to the right.
We use the rules for dividing positive and negative numbers with decimals, too. When dividing signed decimals, first determine the sign of the quotient and then divide as if the numbers were both positive. Finally, write the quotient (that is, the solution) with the appropriate sign.
It may help to review the vocabulary for division:
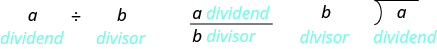
Divide decimal numbers
- Determine the sign of the quotient.
- Make the divisor a whole number by moving the decimal point all the way to the right. Move the decimal point in the dividend the same number of places to the right, writing zeros as needed.
- Divide. Place the decimal point in the quotient above the decimal point in the dividend.
- Write the quotient with the appropriate sign.
example
Divide: [latex]-2.89\div \text{(}3.4\text{)}[/latex]
try it
example
Divide: [latex]-25.65\div \text{(}-0.06\text{)}[/latex]
try it
In the next example we show how to divide two decimals that include negatives.
Now we will divide a whole number by a decimal number.
example
Divide: [latex]4\div 0.05[/latex]
try it
The following example shows how to divide a whole number by a decimal using base ten blocks.
Candela Citations
- Question ID 146607, 146604, 146601,146600. Authored by: Lumen Learning. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Ex: Dividing a Decimal by a Whole Number. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/LkbSiL6uvtU. License: Public Domain: No Known Copyright
- Ex: Dividing Signed Decimals. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/o2ad4UzTlj0. License: CC BY: Attribution
- Ex: Determine the Quotient of a Whole Number and Decimal using Base Ten Blocks. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/LmWzhGvDt58. License: CC BY: Attribution
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@9.757




