Learning Outcomes
- Find the volume and surface area of cylinders
If you have ever seen a can of soda, you know what a cylinder looks like. A cylinder is a solid figure with two parallel circles of the same size at the top and bottom. The top and bottom of a cylinder are called the bases. The height [latex]h[/latex] of a cylinder is the distance between the two bases. For all the cylinders we will work with here, the sides and the height, [latex]h[/latex] , will be perpendicular to the bases.
A cylinder has two circular bases of equal size. The height is the distance between the bases.

Rectangular solids and cylinders are somewhat similar because they both have two bases and a height. The formula for the volume of a rectangular solid, [latex]V=Bh[/latex] , can also be used to find the volume of a cylinder.
For the rectangular solid, the area of the base, [latex]B[/latex] , is the area of the rectangular base, length × width. For a cylinder, the area of the base, [latex]B[/latex], is the area of its circular base, [latex]\pi {r}^{2}[/latex]. The image below compares how the formula [latex]V=Bh[/latex] is used for rectangular solids and cylinders.
Seeing how a cylinder is similar to a rectangular solid may make it easier to understand the formula for the volume of a cylinder.

To understand the formula for the surface area of a cylinder, think of a can of vegetables. It has three surfaces: the top, the bottom, and the piece that forms the sides of the can. If you carefully cut the label off the side of the can and unroll it, you will see that it is a rectangle. See the image below.
By cutting and unrolling the label of a can of vegetables, we can see that the surface of a cylinder is a rectangle. The length of the rectangle is the circumference of the cylinder’s base, and the width is the height of the cylinder.

The distance around the edge of the can is the circumference of the cylinder’s base it is also the length [latex]L[/latex] of the rectangular label. The height of the cylinder is the width [latex]W[/latex] of the rectangular label. So the area of the label can be represented as

To find the total surface area of the cylinder, we add the areas of the two circles to the area of the rectangle.

The surface area of a cylinder with radius [latex]r[/latex] and height [latex]h[/latex], is
[latex]S=2\pi {r}^{2}+2\pi rh[/latex]
Volume and Surface Area of a Cylinder
For a cylinder with radius [latex]r[/latex] and height [latex]h:[/latex]

example
A cylinder has height [latex]5[/latex] centimeters and radius [latex]3[/latex] centimeters. Find 1. the volume and 2. the surface area.
Solution
| Step 1. Read the problem. Draw the figure and label
it with the given information. |
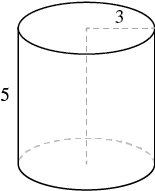 |
| 1. | |
| Step 2. Identify what you are looking for. | The volume of the cylinder |
| Step 3. Name. Choose a variable to represent it. | Let V = volume. |
| Step 4. Translate.
Write the appropriate formula. Substitute. (Use [latex]3.14[/latex] for [latex]\pi[/latex] ) |
[latex]V=\pi {r}^{2}h[/latex]
[latex]V\approx \left(3.14\right)({3}cm)^{2}\cdot 5cm[/latex] |
| Step 5. Solve. | [latex]V\approx 141.3cm^3[/latex] |
| Step 6. Check: We leave it to you to check your calculations. | |
| Step 7. Answer the question. | The volume is approximately [latex]141.3[/latex] cubic centimeters. |
| 2. | |
| Step 2. Identify what you are looking for. | The surface area of the cylinder |
| Step 3. Name. Choose a variable to represent it. | Let S = surface area. |
| Step 4. Translate.
Write the appropriate formula. Substitute. (Use [latex]3.14[/latex] for [latex]\pi[/latex] ) |
[latex]S=2\pi {r}^{2}+2\pi rh[/latex]
[latex]S\approx 2\left(3.14\right)({3}cm)^{2}+2\left(3.14\right)\left(3cm\right)5cm[/latex] |
| Step 5. Solve. | [latex]S\approx 150.72cm^2[/latex] |
| Step 6. Check: We leave it to you to check your calculations. | |
| Step 7. Answer the question. | The surface area is approximately [latex]150.72[/latex] square centimeters. |
try it
example
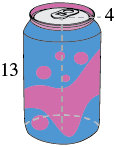
Find 1. the volume and 2. the surface area of a can of soda. The radius of the base is [latex]4[/latex] centimeters and the height is [latex]13[/latex] centimeters. Assume the can is shaped exactly like a cylinder.
try it
The following video shows an example of how to find the volume of a cylinder.
In the next example video we show how to find the surface area of a cylinder.
Candela Citations
- Question ID 146815, 146810. Authored by: Lumen Learning. License: CC BY: Attribution
- Ex: Volume of a Cylinder. Authored by: James Sousa (mathispower4u.com). Located at: https://youtu.be/oDgfx-Kztrk. License: CC BY: Attribution
- Find the Surface Area of a Cylinder. Authored by: James Sousa (mathispower4u.com). Located at: https://youtu.be/CN_7ZxmixXY. License: CC BY: Attribution
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@9.757