Learning Outcomes
- Use the definition of a logarithm to solve logarithmic equations
- Use the rules of logarithms and one-to-one property of logarithms to solve a logarithmic equation
We have already seen that every logarithmic equation [latex]{\mathrm{log}}_{b}\left(x\right)=y[/latex] can be written as the exponential equation [latex]{b}^{y}=x[/latex]. We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.
For example, consider the equation [latex]{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3[/latex]. To solve this equation, we can use rules of logarithms to rewrite the left side in condensed form and then apply the definition of logs to solve for x:
Example
Solve [latex]2\mathrm{ln}x+3=7[/latex].
Analysis of the Solution
The solution for the previous equation was [latex]x={e}^{2}[/latex]; this is often referred to as the exact solution. Sometimes, you may be asked to give an approximation, which would be more useful to someone using the result for a financial, scientific, or engineering application. The approximation for [latex]x={e}^{2}[/latex] can be found with a calculator. [latex]x={e}^{2}\approx{7.4}[/latex]
In general, we can describe using the definition of a logarithm to solve logarithmic equations as follows:
For any algebraic expression S and real numbers b and c, where [latex]b>0,\text{ }b\ne 1[/latex],
Example
Solve [latex]2\mathrm{ln}\left(6x\right)=7[/latex].
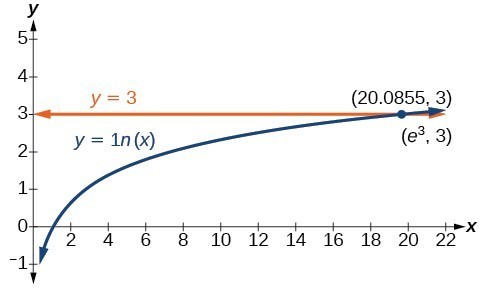
In our next example, we will show you the power of using graphs to analyze solutions to logarithmic equations. By turning each side of the equation into a function and plotting them on the same set of axes, we can see how they interact with each other. In this case, we get a logarithmic function and a horizontal line and find that the solution is the point where the two intersect.
Example
Solve [latex]\mathrm{ln}x=3[/latex].
In the same way that a story can help you understand a complex concept, graphs can help us understand a wide variety of concepts in mathematics. Visual representations of the parts of an equation can be created by turning each side into a function and plotting the functions on the same set of axes.
Use the One-to-One Property of Logarithms to Solve Logarithmic Equations
As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers [latex]x\gt0, S\gt0, T\gt0[/latex] and any positive real number b, where [latex]b\ne 1[/latex],
For example,
So, if [latex]x - 1=8[/latex], then we can solve for x, and we get [latex]x=9[/latex]. To check, we can substitute [latex]x=9[/latex] into the original equation: [latex]{\mathrm{log}}_{2}\left(9 - 1\right)={\mathrm{log}}_{2}\left(8\right)=3[/latex]. In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.
Example
Solve [latex]\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)[/latex].
Check your results.
Note, when solving an equation involving logarithms, always check to see if the answer is correct or if there is an extraneous solution.
In general, we can summarize solving logarithmic equations as follows:
For [latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\text{ if and only if }S=T[/latex]
- Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation has the form [latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T[/latex].
- Use the one-to-one property to set the arguments equal to each other.
- Solve the resulting equation, [latex]S=T[/latex], for the unknown.
Example
Solve [latex]\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}\left(2x+3\right)[/latex].
Analysis of the Solution
There are two solutions: [latex]x=3[/latex] or [latex]x=–1[/latex]. The solution [latex]x=–1[/latex] is negative, but it checks when substituted into the original equation because the argument of the logarithm function is still positive.
In the following video, we show more examples of solving logarithmic equations.
Summary
We can combine the definition of logarithms and algebraic tools used for solving linear equations to solve logarithmic equations. Graphing each side of a logarithmic equation helps you analyze the solution.