Locating and Ordering Decimals With a Number Line

Learning Outcomes

  • Locate decimals on the number line
  • Order decimals

Since decimals are forms of fractions, locating decimals on the number line is similar to locating fractions on the number line.

Exercises

Locate [latex]0.4[/latex] on a number line.

Solution
The decimal [latex]0.4[/latex] is equivalent to [latex]{\Large\frac{4}{10}}[/latex], so [latex]0.4[/latex] is located between [latex]0[/latex] and [latex]1[/latex]. On a number line, divide the interval between [latex]0[/latex] and [latex]1[/latex] into [latex]10[/latex] equal parts and place marks to separate the parts.

Label the marks [latex]0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0[/latex]. We write [latex]0[/latex] as [latex]0.0[/latex] and [latex]1[/latex] as [latex]1.0[/latex], so that the numbers are consistently in tenths. Finally, mark [latex]0.4[/latex] on the number line.

A number line is shown with 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0 labeled. There is a red dot at 0.4.

 

try it

  2. Locate [latex]0.6[/latex] on a number line.

 

example

Locate [latex]-0.74[/latex] on a number line.

 

try it

In the next video we show more examples of how to locate a decimal on the number line.

Order Decimals

Which is larger, [latex]0.04[/latex] or [latex]0.40?[/latex]

If you think of this as money, you know that [latex]$0.40[/latex] (forty cents) is greater than [latex]$0.04[/latex] (four cents). So,

[latex]0.40>0.04[/latex]

In previous chapters, we used the number line to order numbers.

[latex]\begin{array}{}\\ ab\text{ , }a\text{ is greater than }b\text{ when }a\text{ is to the right of }b\text{ on the number line}\hfill \end{array}[/latex]

Where are [latex]0.04[/latex] and [latex]0.40[/latex] located on the number line?

A number line is shown with 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0 labeled. There is a red dot between 0.0 and 0.1 labeled as 0.04. There is another red dot at 0.4.
We see that [latex]0.40[/latex] is to the right of [latex]0.04[/latex]. So we know [latex]0.40>0.04[/latex].

How does [latex]0.31[/latex] compare to [latex]0.308?[/latex] This doesn’t translate into money to make the comparison easy. But if we convert [latex]0.31[/latex] and [latex]0.308[/latex] to fractions, we can tell which is larger.

[latex]0.31[/latex] [latex]0.308[/latex]
Convert to fractions. [latex]{\Large\frac{31}{100}}[/latex] [latex]{\Large\frac{308}{1000}}[/latex]
We need a common denominator to compare them. [latex]{\Large\frac{31\cdot\color{red}{10}}{100\cdot\color{red}{10}}}[/latex] [latex]{\Large\frac{308}{1000}}[/latex]
[latex]{\Large\frac{310}{1000}}[/latex] [latex]{\Large\frac{308}{1000}}[/latex]

Because [latex]310>308[/latex], we know that [latex]{\Large\frac{310}{1000}}>{\Large\frac{308}{1000}}[/latex]. Therefore, [latex]0.31>0.308[/latex].

Notice what we did in converting [latex]0.31[/latex] to a fraction—we started with the fraction [latex]\Large\frac{31}{100}[/latex] and ended with the equivalent fraction [latex]\Large\frac{310}{1000}[/latex]. Converting [latex]\Large\frac{310}{1000}[/latex] back to a decimal gives [latex]0.310[/latex]. So [latex]0.31[/latex] is equivalent to [latex]0.310[/latex]. Writing zeros at the end of a decimal does not change its value.

[latex]{\Large\frac{31}{100}}={\Large\frac{310}{1000}}\text{ and }0.31=0.310[/latex]

If two decimals have the same value, they are said to be equivalent decimals.

[latex]0.31=0.310[/latex]

We say [latex]0.31[/latex] and [latex]0.310[/latex] are equivalent decimals.

Equivalent Decimals

Two decimals are equivalent decimals if they convert to equivalent fractions.

Remember, writing zeros at the end of a decimal does not change its value.

Order decimals

  1. Check to see if both numbers have the same number of decimal places. If not, write zeros at the end of the one with fewer digits to make them match.
  2. Compare the numbers to the right of the decimal point as if they were whole numbers.
  3. Order the numbers using the appropriate inequality sign.

 

example

Order the following decimals using [latex]<\text{ or }\text{>}[/latex]:

  1. [latex]0.64[/latex] ____ [latex]0.6[/latex]
  2. [latex]0.83[/latex] ____ [latex]0.803[/latex]

 

try it

When we order negative decimals, it is important to remember how to order negative integers. Recall that larger numbers are to the right on the number line. For example, because [latex]-2[/latex] lies to the right of [latex]-3[/latex] on the number line, we know that [latex]-2>-3[/latex]. Similarly, smaller numbers lie to the left on the number line. For example, because [latex]-9[/latex] lies to the left of [latex]-6[/latex] on the number line, we know that [latex]-9<-6[/latex]. 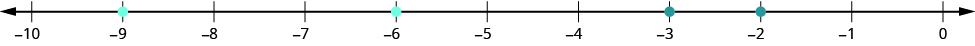A number line is shown with integers from negative 10 to 0. Blue dots are placed on negative nine and negative six. Red dots are placed at negative two and negative three.
If we zoomed in on the interval between [latex]0[/latex] and [latex]-1[/latex], we would see in the same way that [latex]-0.2>-0.3\text{ and}-0.9<-0.6[/latex].

example

Use [latex]<\text{or}>[/latex]; to order. [latex]-0.1[/latex] ____ [latex]- 0.8[/latex].

 

try it

In the following video lesson we show how to order decimals using inequality notation by comparing place values, and by using fractions.