Now we are ready to plot fractions on the number line. This will help us visualize fractions and understand their values.

Let us locate [latex]{\dfrac{1}{5}, \dfrac{4}{5}}, 3, 3{\dfrac{1}{3}, \dfrac{7}{4}, \dfrac{9}{2}}, 5[/latex], and [latex]{\dfrac{8}{3}}[/latex] on the number line.

We will start with the whole numbers [latex]3[/latex] and [latex]5[/latex] because they are the easiest to plot.

The proper fractions listed are [latex]{\dfrac{1}{5}}[/latex] and [latex]{\dfrac{4}{5}}[/latex]. We know proper fractions have values less than one, so [latex]{\dfrac{1}{5}}[/latex] and [latex]{\dfrac{4}{5}}[/latex] are located between the whole numbers [latex]0[/latex] and [latex]1[/latex]. The denominators are both [latex]5[/latex], so we need to divide the segment of the number line between [latex]0[/latex] and [latex]1[/latex] into five equal parts. We can do this by drawing four equally spaced marks on the number line, which we can then label as [latex]{\dfrac{1}{5},\dfrac{2}{5},\dfrac{3}{5}}[/latex], and [latex]{\dfrac{4}{5}}[/latex].

Now plot points at [latex]{\dfrac{1}{5}}[/latex] and [latex]{\dfrac{4}{5}}[/latex].

The only mixed number to plot is [latex]3{\dfrac{1}{3}}[/latex]. Between what two whole numbers is [latex]3{\dfrac{1}{3}}[/latex]? Remember that a mixed number is a whole number plus a proper fraction, so [latex]3{\dfrac{1}{3}}>3[/latex]. Since it is greater than [latex]3[/latex], but not a whole unit greater, [latex]3{\dfrac{1}{3}}[/latex] is between [latex]3[/latex] and [latex]4[/latex]. We need to divide the portion of the number line between [latex]3[/latex] and [latex]4[/latex] into three equal pieces (thirds) and plot [latex]3{\dfrac{1}{3}}[/latex] at the first mark.

Finally, look at the improper fractions [latex]{\dfrac{7}{4},\dfrac{9}{2}}[/latex], and [latex]{\dfrac{8}{3}}[/latex]. Locating these points will be easier if you change each of them to a mixed number.

[latex]{\dfrac{7}{4}}=1{\dfrac{3}{4}},{\dfrac{9}{2}}=4{\dfrac{1}{2}},{\dfrac{8}{3}}=2{\dfrac{2}{3}}[/latex]

Here is the number line with all the points plotted.

Example

Locate and label the following on a number line: [latex]{\dfrac{3}{4},\dfrac{4}{3},\dfrac{5}{3}},4{\dfrac{1}{5}}[/latex], and [latex]{\dfrac{7}{2}}[/latex].

Solution:
Start by locating the proper fraction [latex]{\dfrac{3}{4}}[/latex]. It is between [latex]0[/latex] and [latex]1[/latex]. To do this, divide the distance between [latex]0[/latex] and [latex]1[/latex] into four equal parts. Then plot [latex]{\dfrac{3}{4}}[/latex].

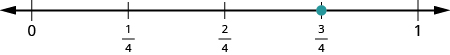
Next, locate the mixed number [latex]4{\dfrac{1}{5}}[/latex]. It is between [latex]4[/latex] and [latex]5[/latex] on the number line. Divide the number line between [latex]4[/latex] and [latex]5[/latex] into five equal parts, and then plot [latex]4{\dfrac{1}{5}}[/latex] one-fifth of the way between [latex]4[/latex] and [latex]5[/latex] .

Now locate the improper fractions [latex]{\dfrac{4}{3}}[/latex] and [latex]{\dfrac{5}{3}}[/latex]. It is easier to plot them if we convert them to mixed numbers first.

[latex]{\dfrac{4}{3}}=1{\dfrac{1}{3}},{\dfrac{5}{3}}=1{\dfrac{2}{3}}[/latex]
Divide the distance between [latex]1[/latex] and [latex]2[/latex] into thirds.

Next let us plot [latex]{\dfrac{7}{2}}[/latex]. We write it as a mixed number, [latex]{\dfrac{7}{2}}=3{\dfrac{1}{2}}[/latex] . Plot it between [latex]3[/latex] and [latex]4[/latex].

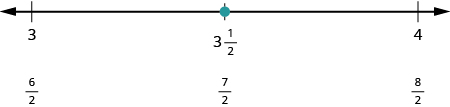
The number line shows all the numbers located on the number line.

Watch the following video to see more examples of how to locate fractions on a number line.

We previously defined the opposite of a number. It is the number that is the same distance from zero on the number line but on the opposite side of zero. We saw, for example, that the opposite of [latex]7[/latex] is [latex]-7[/latex] and the opposite of [latex]-7[/latex] is [latex]7[/latex].

Fractions have opposites, too. The opposite of [latex]{\dfrac{3}{4}}[/latex] is [latex]-{\dfrac{3}{4}}[/latex]. It is the same distance from [latex]0[/latex] on the number line, but on the opposite side of [latex]0[/latex].

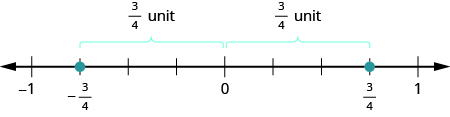
Thinking of negative fractions as the opposite of positive fractions will help us locate them on the number line. To locate [latex]-{\dfrac{15}{8}}[/latex] on the number line, first think of where [latex]{\dfrac{15}{8}}[/latex] is located. It is an improper fraction, so we first convert it to the mixed number [latex]1{\dfrac{7}{8}}[/latex] and see that it will be between [latex]1[/latex] and [latex]2[/latex] on the number line. So its opposite, [latex]-{\dfrac{15}{8}}[/latex], will be between [latex]-1[/latex] and [latex]-2[/latex] on the number line.

Example

Locate and label the following on the number line: [latex]{\dfrac{1}{4}},-{\dfrac{1}{4}},1{\dfrac{1}{3}},-1{\dfrac{1}{3}},{\dfrac{5}{2}}[/latex], and [latex]-{\dfrac{5}{2}}[/latex].

Show Solution

Solution:
Draw a number line. Mark [latex]0[/latex] in the middle and then mark several units to the left and right.

To locate [latex]{\dfrac{1}{4}}[/latex], divide the interval between [latex]0[/latex] and [latex]1[/latex] into four equal parts. Each part represents one-quarter of the distance. So plot [latex]{\dfrac{1}{4}}[/latex] at the first mark.

To locate [latex]-{\dfrac{1}{4}}[/latex], divide the interval between [latex]0[/latex] and [latex]-1[/latex] into four equal parts. Plot [latex]-{\dfrac{1}{4}}[/latex] at the first mark to the left of [latex]0[/latex].

Since [latex]1{\dfrac{1}{3}}[/latex] is between [latex]1[/latex] and [latex]2[/latex], divide the interval between [latex]1[/latex] and [latex]2[/latex] into three equal parts. Plot [latex]1{\dfrac{1}{3}}[/latex] at the first mark to the right of [latex]1[/latex]. Then since [latex]-1{\dfrac{1}{3}}[/latex] is the opposite of [latex]1{\dfrac{1}{3}}[/latex] it is between [latex]-1[/latex] and [latex]-2[/latex]. Divide the interval between [latex]-1[/latex] and [latex]-2[/latex] into three equal parts. Plot [latex]-1{\dfrac{1}{3}}[/latex] at the first mark to the left of [latex]-1[/latex].

To locate [latex]{\dfrac{5}{2}}[/latex] and [latex]-{\dfrac{5}{2}}[/latex], it may be helpful to rewrite them as the mixed numbers [latex]2{\dfrac{1}{2}}[/latex] and [latex]-2{\dfrac{1}{2}}[/latex].

Since [latex]2{\dfrac{1}{2}}[/latex] is between [latex]2[/latex] and [latex]3[/latex], divide the interval between [latex]2[/latex] and [latex]3[/latex] into two equal parts. Plot [latex]{\dfrac{5}{2}}[/latex] at the mark. Then since [latex]-2{\dfrac{1}{2}}[/latex] is between [latex]-2[/latex] and [latex]-3[/latex], divide the interval between [latex]-2[/latex] and [latex]-3[/latex] into two equal parts. Plot [latex]-{\dfrac{5}{2}}[/latex] at the mark.

In the next video we give more examples of how to locate negative and positive fractions on a number line.

Order Fractions and Mixed Numbers

We can use the inequality symbols to order fractions. Remember that [latex]a>b[/latex] means that [latex]a[/latex] is to the right of [latex]b[/latex] on the number line. As we move from left to right on a number line, the values increase.

In the following video we show another example of how to order integers, fractions and mixed numbers using inequality symbols.

Contribute!

Improve this pageLearn More