Learning Outcomes
- Translate word phrases into mathematical expressions representing multiplication
- Solve word problems by using multiplication
Translate Word Phrases to Math Notation
Earlier in this section, we translated math notation into words. Now we’ll reverse the process and translate word phrases into math notation. Some of the words that indicate multiplication are given in the table below.
| Operation | Word Phrase | Example | Expression |
|---|---|---|---|
| Multiplication | times
product twice |
[latex]3[/latex] times [latex]8[/latex]
the product of [latex]3[/latex] and [latex]8[/latex] twice [latex]4[/latex] |
[latex]3\times 8,3\cdot 8,\left(3\right)\left(8\right)[/latex]
[latex]\left(3\right)8,\text{ or }8\left(3\right)[/latex] [latex]2\cdot 4[/latex] |
example
Translate and simplify: the product of [latex]12[/latex] and [latex]27[/latex].
Solution:
The word product tells us to multiply. The words of [latex]12[/latex] and [latex]27[/latex] tell us the two factors.
| the product of [latex]12[/latex] and [latex]27[/latex] | |
| Translate. | [latex]12\cdot 27[/latex] |
| Multiply. | [latex]324[/latex] |
example
Translate and simplify: twice two hundred eleven.
Multiply Whole Numbers in Applications
We will use the same strategy we used previously to solve applications of multiplication. First, we need to determine what we are looking for. Then we write a phrase that gives the information to find it. We then translate the phrase into math notation and simplify to get the answer. Finally, we write a sentence to answer the question.
example
Humberto bought [latex]4[/latex] sheets of stamps. Each sheet had [latex]20[/latex] stamps. How many stamps did Humberto buy?
example
When Rena cooks rice, she uses twice as much water as rice. How much water does she need to cook [latex]4[/latex] cups of rice?
example
Van is planning to build a patio. He will have [latex]8[/latex] rows of tiles, with [latex]14[/latex] tiles in each row. How many tiles does he need for the patio?
If we want to know the size of a wall that needs to be painted or a floor that needs to be carpeted, we will need to find its area. The area is a measure of the amount of surface that is covered by the shape. Area is measured in square units. We often use square inches, square feet, square centimeters, or square miles to measure area. A square centimeter is a square that is one centimeter (cm.) on a side. A square inch is a square that is one inch on each side, and so on.

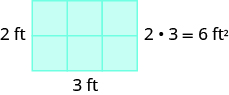
For a rectangular figure, the area is the product of the length and the width. The figure below shows a rectangular rug with a length of [latex]2[/latex] feet and a width of [latex]3[/latex] feet. Each square is [latex]1[/latex] foot wide by [latex]1[/latex] foot long, or [latex]1[/latex] square foot. The rug is made of [latex]6[/latex] squares. The area of the rug is [latex]6[/latex] square feet.
The area of a rectangle is the product of its length and its width, or [latex]6[/latex] square feet.
example
Jen’s kitchen ceiling is a rectangle that measures [latex]9[/latex] feet long by [latex]12[/latex] feet wide. What is the area of Jen’s kitchen ceiling?
In the following video, we show another example of using multiplication to solve application problems.

