Plotting Points on the Coordinate Plane

Learning Outcomes

  • Identify quadrants on the coordinate plane
  • Plot points on a rectangular coordinate system

Introduction to the Coordinate Plane

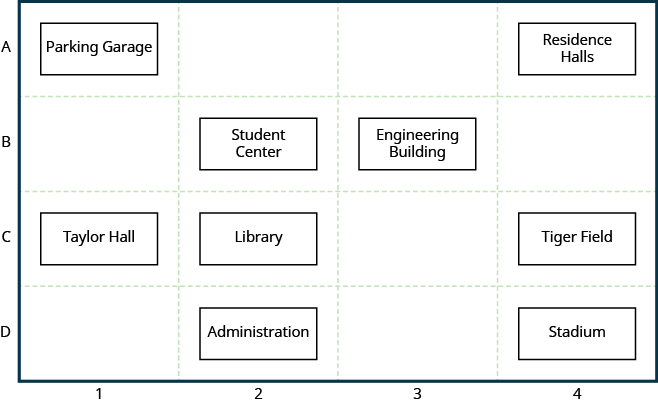
You have likely used a coordinate plane before. For example, have you ever used a gridded overlay to map the position of an object or location? Many maps, such as the Campus Map shown below, use a grid system to identify locations. This map uses a horizontal and vertical grid to convey information about an object’s location. Do you see the numbers [latex]1,2,3[/latex], and [latex]4[/latex] across the top and bottom of the map and the letters A, B, C, and D along the sides? Every location on the map can be identified by a number and a letter.

The general location of any item on this map can be found by using the letter and number of its grid square. For example, the Student Center is in section 2B. It is located in the grid section above the number [latex]2[/latex] and next to the letter B. In which grid section is the Stadium? The Stadium is in section 4D.

The figure shows a labeled grid representing the Campus Map. The columns are labeled 1 through 4 and the rows are labeled A through D. At position A-1 is the title Parking Garage. At position A-4 is a rectangle labeled Residence Halls. At position B-2 is a rectangle labeled Student Center. At position B-3 is a rectangle labeled Engineering Building. At position C-1 is a rectangle labeled Taylor Hall. At position C-2 is a rectangle labeled Library. At position C-4 is a rectangle labeled Tiger Field. At position D-4 is a rectangle labeled Stadium.

example

Use the map above.

  1. Find the grid section of the Residence Halls.
  2. What is located in grid section 4C?

 

Rectangular Coordinate System

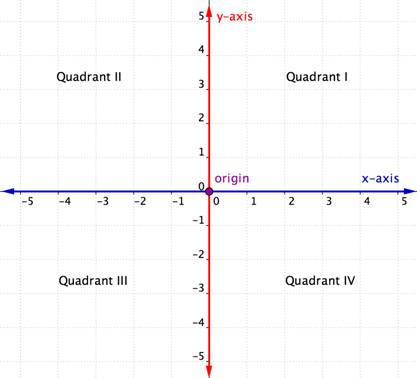
The coordinate plane has similar elements to the grid shown above.  Look at the Rectangular Coordinate System show in the box below. It consists of a horizontal axis and a vertical axis, number lines that intersect at right angles. (They are perpendicular to each other.)

The horizontal axis in the coordinate plane is called the [latex]x-axis[/latex]. The vertical axis is called the [latex]y-axis[/latex]. The point at which the two axes intersect is called the origin. The origin is at [latex]0[/latex] on the [latex]x-axis[/latex] and [latex]0[/latex] on the [latex]y-axis[/latex].

The intersecting x- and y-axes of the coordinate plane divide it into four sections. These four sections are called quadrants. Quadrants are named using the Roman numerals I, II, III, and IV beginning with the top right quadrant and moving counter clockwise.

The rectangular coordinate system

A graph with an x-axis running horizontally and a y-axis running vertically. The location where these axes cross is labeled the origin, and is the point zero, zero. The axes also divide the graph into four equal quadrants. The top right area is quadrant one. The top left area is quadrant two. The bottom left area is quadrant three. The bottom right area is quadrant four.

Locations on the coordinate plane are described as ordered pairs. An ordered pair tells you the location of a point by relating the point’s location along the x-axis (the first value of the ordered pair) and along the [latex]y-axis[/latex] (the second value of the ordered pair).

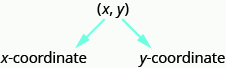
In an ordered pair, such as [latex](x, y)[/latex], the first value is called the x-coordinate and the second value is the y-coordinate. Note that the x-coordinate is listed before the y-coordinate. Since the origin has an x-coordinate of [latex]0[/latex] and a y-coordinate of [latex]0[/latex], its ordered pair is written [latex](0, 0)[/latex].

Ordered Pair

An ordered pair, [latex]\left(x,y\right)[/latex] gives the coordinates of a point in a rectangular coordinate system.

[latex]\begin{array}{c}\text{The first number is the }x\text{-coordinate}.\hfill \\ \text{The second number is the }y\text{-coordinate}.\hfill \end{array}[/latex]

The ordered pair x y is labeled with the first coordinate x labeled as “x-coordinate” and the second coordinate y labeled as “y-coordinate”

Plotting Points in the Coordinate Plane

Now that you know the components of a rectangular system, let’s learn how to plot ordered pairs, that is locate a point on the coordinate system given an ordered pair. Just remember, the process start at the origin—the beginning!

Let’s try locating the point [latex]\left(2,5\right)[/latex]. In this ordered pair, the [latex]x[/latex]-coordinate is [latex]2[/latex] and the [latex]y[/latex]-coordinate is [latex]5[/latex] .

We start by locating the [latex]x[/latex] value, [latex]2[/latex], on the [latex]x\text{-axis.}[/latex] Then we lightly sketch a vertical line through [latex]x=2[/latex], as shown in the image below.

The graph shows the x y-coordinate plane. The x and y-axis each run from -6 to 6. There is a vertical dotted line passing through 2 on the x-axis.
Now we locate the [latex]y[/latex] value, [latex]5[/latex], on the [latex]y[/latex] -axis and sketch a horizontal line through [latex]y=5[/latex] . The point where these two lines meet is the point with coordinates [latex]\left(2,5\right)[/latex]. We plot the point there, as shown in the image below.

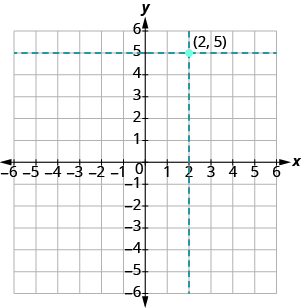
The graph shows the x y-coordinate plane. The x and y-axis each run from -6 to 6. An arrow starts at the origin and extends right to the number 2 on the x-axis. An arrow starts at the end of the first arrow at 2 on the x-axis and goes vertically 5 units to a point labeled “2, 5” in parentheses.

Reminder:  Any ordered pair, such as (2,5), represents one single point on the graph.

example

Plot [latex]\left(1,3\right)[/latex] and [latex]\left(3,1\right)[/latex] in the same rectangular coordinate system.

 

Now, let’s take another look at how to plot the ordered pair (1,3).  The method show below is slightly different from the method shown above, but yields the same result.

Example

Plot the point [latex](1, 3)[/latex].

 

try it

 

In the previous examples, both the x- and y-coordinates were positive. When one (or both) of the coordinates of an ordered pair is negative, you will need to move in the negative direction along one or both axes. Consider the example below in which both coordinates are negative.

Example

Plot the point [latex](−4,−2)[/latex].

Graph with blue arrow pointing from origin to four units to the left. A red arrow points down 2 spaces to the point negative 4, negative 2.

The x-coordinate is [latex]−4[/latex] because it comes first in the ordered pair. Start at the origin and move [latex]4[/latex] units in a negative direction (left) along the x-axis.

The y-coordinate is [latex]−2[/latex] because it comes second in the ordered pair. Now move [latex]2[/latex] units in a negative direction (down). If you look over to the y-axis, you should be lined up with [latex]−2[/latex] on that axis.

Now draw a point at that location and label it.

The steps for plotting a point are summarized below.

Steps for Plotting an Ordered Pair (x, y) in the Coordinate Plane

  • Determine the x-coordinate. Beginning at the origin, move horizontally, the direction of the x-axis, the distance given by the x-coordinate. If the x-coordinate is positive, move to the right; if the x-coordinate is negative, move to the left.
  • Determine the y-coordinate. Beginning at the x-coordinate, move vertically, the direction of the y-axis, the distance given by the y-coordinate. If the y-coordinate is positive, move up; if the y-coordinate is negative, move down.
  • Draw a point at the ending location. Label the point with the ordered pair.
  • An ordered pair is represented by a single point on the graph.

example

How do the signs affect the location of the points?

Plot each point:

1. [latex]\left(-5,2\right)[/latex]
2. [latex]\left(-5,-2\right)[/latex]
3. [latex]\left(5,2\right)[/latex]
4. [latex]\left(5,-2\right)[/latex]

 

try it

Watch the video below for more examples of how to plot ordered pairs.

Identify quadrants and use them to plot points

Recall that when we described the rectangular coordinate system above, we mentioned the four quadrants, quadrants I, II, III, and IV.  These quadrants can be useful for locating points because ordered pairs within any particular quadrant share certain characteristics. Look at each quadrant in the graph below. What do you notice about the signs of the x- and y-coordinates of the points within each quadrant?

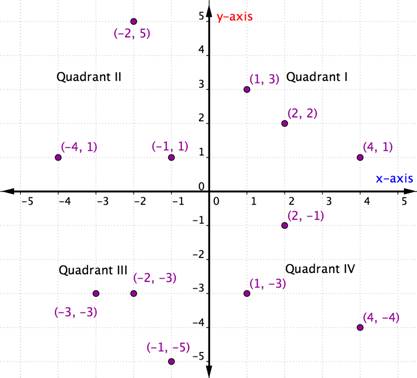
A graph with many plotted points in different quadrants. Quadrant 1 has the point (1,3); the point (2,2); and the point (4,1). Quadrant 2 has the point negative 1, one; the point negative 2, 5; and the point negative 4, one. Quadrant 3 has the point negative 2, negative 3; the point negative 3, negative 3; and the point negative 1, negative 5. Quadrant 4 has the point 2, negative 1; the point 1, negative 3; and the point 4, negative 4.

Within each quadrant, the signs of the x-coordinates and y-coordinates of each ordered pair are the same. They also follow a pattern, which is outlined in the table below.

Quadrant General Form of Point in this Quadrant Example Description
I [latex](+,+)[/latex] [latex](5,4)[/latex] Starting from the origin, go along the x-axis in a positive direction (right) and along the y-axis in a positive direction (up).
II [latex](−,+)[/latex] [latex](−5,4)[/latex] Starting from the origin, go along the x-axis in a negative direction (left) and along the y-axis in a positive direction (up).
III [latex](−,−)[/latex] [latex](−5,−4)[/latex] Starting from the origin, go along the x-axis in a negative direction (left) and along the y-axis in a negative direction (down).
IV [latex](+,−)[/latex] [latex](5,−4)[/latex] Starting from the origin, go along the x-axis in a positive direction (right) and along the y-axis in a negative direction (down).

Once you know about the quadrants in the coordinate plane, you can determine the quadrant of an ordered pair without even graphing it by looking at the chart above. Here’s another way to think about it.

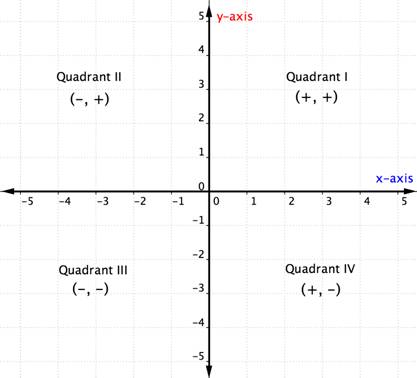
Graph with quadrants. Quadrant 1 is positive, positive. Quadrant 2 is negative, positive. Quadrant 3 is negative, negative. Quadrant 4 is positive, negative.

The example below details how to determine the quadrant location of a point just by thinking about the signs of its coordinates. Thinking about the quadrant location before plotting a point can help you prevent a mistake. It is also useful knowledge for checking that you have plotted a point correctly.

Example

In which quadrant is the point [latex](−7,10)[/latex] located?

Example

In which quadrant is the point [latex](−10,−5)[/latex] located?

 

Exercises

Plot each point in the rectangular coordinate system and identify the quadrant in which the point is located:

1. [latex]\left(-1,3\right)[/latex]
2. [latex]\left(-3,-4\right)[/latex]
3. [latex]\left(2,-3\right)[/latex]
4. [latex]\left(3,{\dfrac{5}{2}}\right)[/latex]

 

try it

 

You can watch the video below to see more examples of how to identify the quadrant that a point is located in.

 Points on the Axes

What happens if an ordered pair has an x– or y-coordinate of zero? The example below shows the graph of the ordered pair [latex](0,4)[/latex]. Notice how the point [latex]\left(0,4\right)[/latex] is located on the [latex]y[/latex]-axis.

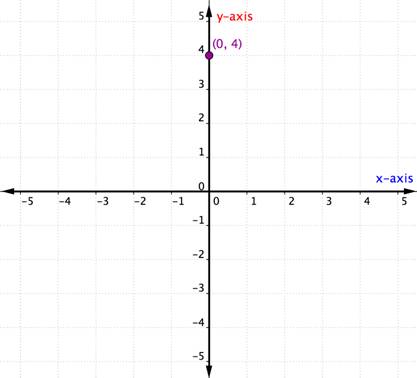
Graph of the point (0,4). The point is on the y-axis.

A point located on one of the axes is not considered to be in a quadrant. It is simply on one of the axes. Whenever the x-coordinate is [latex]0[/latex], the point is located on the y-axis. Similarly, any point that has a y-coordinate of [latex]0[/latex] will be located on the x-axis.

Points on the Axes

Points with a [latex]y\text{-coordinate}[/latex] equal to [latex]0[/latex] are on the [latex]x\text{-axis}[/latex], and have coordinates [latex]\left(a,0\right)[/latex].

Points with an [latex]x\text{-coordinate}[/latex] equal to [latex]0[/latex] are on the [latex]y\text{-axis}[/latex], and have coordinates [latex]\left(0,b\right)[/latex].

What is the ordered pair of the point where the axes cross, or interesect? At that point both coordinates are zero, so its ordered pair is [latex]\left(0,0\right)[/latex] . The point has a special name. It is called the origin.

The Origin

The point [latex]\left(0,0\right)[/latex] is called the origin. It is the point where the x-axis and y-axis intersect.

ExAMPLE

Plot each point on a coordinate grid:

1. [latex]\left(0,5\right)[/latex]
2. [latex]\left(4,0\right)[/latex]
3. [latex]\left(-3,0\right)[/latex]
4. [latex]\left(0,0\right)[/latex]
5. [latex]\left(0,-1\right)[/latex]

 

TRY IT