Cost and Revenue Problems

Learning Outcomes

Solve cost and revenue problems

A skateboard manufacturer introduces a new line of boards. The manufacturer tracks its costs, which is the amount it spends to produce the boards, and its revenue, which is the amount it earns through sales of its boards. How can the company determine if it is making a profit with its new line? How many skateboards must be produced and sold before a profit is possible?

Skateboarders at a skating rink by the beach.

Using what we have learned about systems of equations, we can answer these questions. The skateboard manufacturer’s revenue equation is the equation used to calculate the amount of money that comes into the business. It can be represented as [latex]y=xp[/latex], where [latex]x=[/latex] quantity and [latex]p=[/latex] price. The revenue equation is shown in orange in the graph below.

The cost equation is the equation used to calculate the costs of doing business. It includes fixed costs, such as rent and salaries, and variable costs, such as utilities. The cost equation is shown in blue in the graph below. The [latex]x[/latex] -axis represents quantity in hundreds of units. The [latex]y-axis[/latex] represents both cost and revenue in hundreds of dollars. We won’t learn how to write a cost equation in this example, they will be given to you. If you take any business or economics courses, you will learn more about how to write a cost equation.

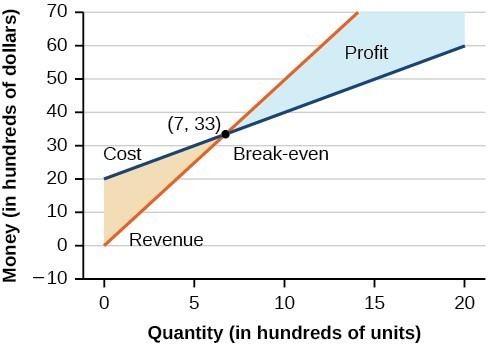
A graph showing money in hundreds of dollars on the y axis and quantity in hundreds of units on the x axis. A line representing cost and a line representing revenue cross at the point (7,33), which is marked break-even. The shaded space between the two lines to the right of the break-even point is labeled profit.

The point at which the two lines intersect is called the break-even point, we learned that this is the solution to the system of linear equations that in this case comprise the cost and revenue equations.

Read the axes of the graph carefully, note that quantity is in hundreds, and money is in thousands. The solution to the graphed system is [latex](7, 33)[/latex]. This means that if [latex]700[/latex] units are produced, the cost to make them is [latex]$3,300[/latex] and the revenue is also [latex]$3,300[/latex]. In other words, the company breaks even if they produce and sell [latex]700[/latex] units. They neither make money nor lose money.

The shaded region to the right of the break-even point represents quantities for which the company makes a profit. The shaded region to the left represents quantities for which the company suffers a loss.

Example

A business wants to manufacture bike frames. Before they start production, they need to make sure they can make a profit with the materials and labor force they have. Their accountant has given them a cost equation of [latex]y=0.85x+35,000[/latex] and a revenue equation of [latex]y=1.55x[/latex]:

Interpret [latex]x[/latex] and [latex]y[/latex] for the cost equation
Interpret [latex]x[/latex] and [latex]y[/latex] for the revenue equation

Show Solution

Equation Type	[latex]x[/latex] represents	[latex]y[/latex] represents
Revenue Eqn.	number of frames	amount of money made selling frames
Cost Eqn.	number of frames	cost for making frames

Example

Given the same cost and revenue equations from the previous example, find the break-even point for the bike manufacturer. Interpret the solution with words.

Cost: [latex]y=0.85x+35,000[/latex]

Revenue: [latex]y=1.55x[/latex]

Show Solution

Read and Understand: We want the break even point for this system that represents cost and revenue. This means we want to find where the two lines cross, and we have learned a few different methods for doing this because this is the solution to the system of equations! Substitution looks like the easiest method since the revenue equation is already solved for [latex]y[/latex], [latex]y=1.55x[/latex].

Define and Translate: Write the system of equations.

[latex]\begin{array}{l}\\ y=0.85x+35,000\hfill \\ y=1.55x\hfill \end{array}\\[/latex]

Write and Solve: The equations are already written for us, so we just need to solve the system using substitution.

Substitute the expression [latex]0.85x+35,000[/latex] from the first equation into the second equation and solve for [latex]x[/latex].
[latex]\begin{array}{r}0.85x+35,000=1.55x\\ 35,000=0.7x\,\,\,\\ 50,000=x\,\,\,\,\,\,\,\,\,\,\end{array}\\[/latex]
Then, we substitute [latex]x=50,000[/latex] into either the cost equation or the revenue equation.
[latex]1.55\left(50,000\right)=77,500\\[/latex]
The break-even point is [latex]\left(50,000,77,500\right)[/latex].

Check and Interpret:

The solution to this system is[latex]\left(50,000,77,500\right)[/latex], but what does that mean? Think of a point as [latex]\left(x,y\right)[/latex], where in this case x is the quantity of bikes manufactured and [latex]y[/latex] is an amount of money. For our system [latex]y[/latex] represents two different things and [latex]x[/latex] represents one thing. Refer to the table we made in the first example, shown below:

Equation Type	[latex]x[/latex] represents	[latex]y[/latex] represents
Revenue Eqn.	number of frames	amount of money made selling frames
Cost Eqn.	number of frames	cost for making frames

Let’s interpret the solution with respect to the Cost equation first. [latex]x = 50,000[/latex] and [latex]y = 77,500[/latex]. Using our table, we can translate this as “the cost for producing [latex]50,000[/latex] bike frames is [latex]$75,500[/latex]“.

In the same way, the Revenue equation can be interpreted as “the amount of money the company makes from selling [latex]50,000[/latex] bike frames is [latex]$77,500[/latex]“.

Try It

In our last video you will see an example of how to find the break even point for a small snow cone business.

We have seen that systems of linear equations and inequalities can help to define market behaviors that are very helpful to businesses. The intersection of cost and revenue equations gives the break even point, and also helps define the region for which a company will make a profit.

Contribute!

Did you have an idea for improving this content? We’d love your input.

Improve this page Learn More

Module 16: Linear Systems

Learning Outcomes

Example

Example

Check and Interpret:

Try It

Contribute!