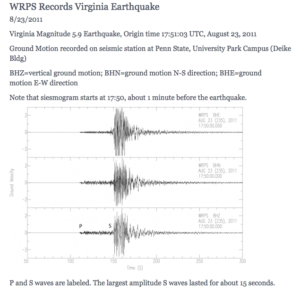
Ground Motion recorded on seismic station at Penn State, University Park Campus (Deike Bldg).

In the beginning of this module, we left Joan with a plan to try and stump her grandfather, the geologist, with the following math problem.

He was so excited to have found something he and Joan could talk about; he beamed when he saw that she had a problem for him to solve.

“I probably knew how to solve that at one time, but it has been a long time,” said grandpa. “Will you show me?”

First, Joan explained to her grandpa that the goal of the problem was to get the argument out of the logarithm. She remembered that a logarithm is an exponent, so her first step was to rewrite the logarithm as an exponential:

[latex]\begin{array}{l}8.5=\mathrm{log}\left(\frac{A}{A_{0}}\right)\\{10}^{8.5}=\frac{A}{A_{0}}\\{10}^{8.5}\cdot{A_{0}}={A}\end{array}[/latex]

Joan entered [latex]{10}^{8.5}[/latex] into a calculator and got the following number:

[latex]316,227,766.017[/latex]

Wow, the amplitude of the waves that caused the Alaska earthquake of [latex]1964[/latex] was [latex]3[/latex] million times greater than the baseline reading!

When working with values that are very large or very small, it is very helpful to work in logarithmic or exponential scales.  It helps scientists be able to avoid having to do calculations with massive numbers.  Additionally, it makes comparisons between different measurements easier to understand.