At the beginning of the module, Joan had applied for a credit card with airmiles so she could pay her regular bills with it. Her hope was to build up enough miles to take a trip. Joan has planned to use her air miles card for the following things each month:
- gas = [latex]$30[/latex]
- car insurance = [latex]$40[/latex]
- mobile phone bill = [latex]$65[/latex]
- groceries = [latex]$150[/latex]
- entertainment – restaurants, movies, and live music = [latex]$50[/latex]
The total monthly expenses she plans to put on her card is [latex]$335[/latex].
Each dollar she spends gives her [latex]1.25[/latex] air miles, and she expects to need about [latex]1200[/latex] air miles to buy the ticket she wants. For signing up, the card gave Joan [latex]100[/latex] free miles.
Help Joan plan for her trip by figuring out how many months she needs to pay her bills with her card before she has enough air miles. Because she earns a fixed amount of air miles for each dollar spent, this is a good candidate for a linear function.
Since we know the amount of air miles earned depends on the number of dollars spent, we can write a function with an input of dollars:
[latex]A(d)=\text{Number of air miles earned as a function of dollars spent}[/latex]
The initial amount of air miles Joan has is [latex]100[/latex], so our function will look like:
[latex]A(d)=100+1.25d[/latex]
Since Joan needs to earn 1200 air miles to buy the ticket she wants, set the function [latex]A(d)=1200[/latex].
[latex]1200=100+1.25d[/latex]
[latex]1100=1.25d[/latex]
[latex]880=d[/latex]
Joan needs to spend $880 before she has enough air miles to buy the ticket she wants. Divide $880 by Joan’s monthly expenses of $335 to determine the number of months Joan needs to pay her bills with her card before having enough air miles.
[latex]\dfrac{880}{335}\approx2.63[/latex]
Since the answer has to be in months and two months would not earn Joan enough air miles, Joan would need to pay her bills for three months with her card before having enough air miles to purchase her ticket.
We began this module by considering how polynomials can be used by computers to create digital images (remember the dolphin?). Let us close with a different example of polynomials in real life, the profits of a cell phone company. In the following polynomial function, the variable [latex]x[/latex] represents the number of phones manufactured.
[latex]P(x)=-0.09x^2+5000x-750,000[/latex]
Using an online graphing calculator, we generated the graph of the profit equation as seen below.
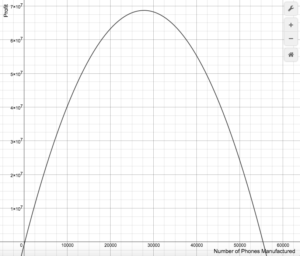
The x-axis represents the number of phones manufactured, and the y-axis represents the profit earned by the company. Because the company must invest money into machinery and workforce to manufacture phones, when no phones have been made, the profit for the company is negative. In other words, the point [latex](0,-750,000)[/latex] represents no phones made and [latex]$750,000[/latex] invested.
The top of the curve represents the “sweet spot” that many business would like to achieve between making and spending money. Using some tools from later math classes, we can find that the maximum amount of profit that can be gained from producing [latex]27,777[/latex] phones.
Polynomials have many practical uses and have been studied widely by mathematicians for many years. Our vast knowledge of how they behave mixed with high speed computing allows us to continue to find even more uses for them.
