Learning Outcomes
- Divide a fraction by a whole number
- Divide a fraction by a fraction
Divide Fractions
There are times when you need to use division to solve a problem. For example, if painting one coat of paint on the walls of a room requires [latex]3[/latex] quarts of paint and you have a bucket that contains [latex]6[/latex] quarts of paint, how many coats of paint can you paint on the walls? You divide [latex]6[/latex] by [latex]3[/latex] for an answer of [latex]2[/latex] coats. There will also be times when you need to divide by a fraction. Suppose painting a closet with one coat only required [latex]\dfrac{1}{2}[/latex] quart of paint. How many coats could be painted with the 6 quarts of paint? To find the answer, you need to divide [latex]6[/latex] by the fraction, [latex]\dfrac{1}{2}[/latex].
Divide a Fraction by a Whole Number
When you divide by a whole number, you are also multiplying by the reciprocal. Review how to find a reciprocal here. In the painting example where you need [latex]3[/latex] quarts of paint for a coat and have [latex]6[/latex] quarts of paint, you can find the total number of coats that can be painted by dividing [latex]6[/latex] by [latex]3[/latex], [latex]6\div3=2[/latex]. You can also multiply [latex]6[/latex] by the reciprocal of [latex]3[/latex], which is [latex]\dfrac{1}{3}[/latex], so the multiplication problem becomes
[latex]\dfrac{6}{1}\cdot\dfrac{1}{3}=\dfrac{6}{3}=\normalsize2[/latex]
Dividing is Multiplying by the Reciprocal
For all division, you can turn the operation into multiplication by using the reciprocal. Dividing is the same as multiplying by the reciprocal.
If you have a recipe that needs to be divided in half, you can divide each ingredient by [latex]2[/latex], or you can multiply each ingredient by [latex]\dfrac{1}{2}[/latex] to find the new amount.
If you have [latex]\dfrac{3}{4}[/latex] of a candy bar and need to divide it among [latex]5[/latex] people, each person gets [latex]\dfrac{1}{5}[/latex] of the available candy:
[latex]\dfrac{1}{5}\normalsize\text{ of }\dfrac{3}{4}=\dfrac{1}{5}\cdot\dfrac{3}{4}=\dfrac{3}{20}[/latex]
Each person gets [latex]\dfrac{3}{20}[/latex] of a whole candy bar.
If you have [latex]\dfrac{3}{2}[/latex] of a pizza left over, how can you divide what is left (the red shaded region) among [latex]6[/latex] people fairly?
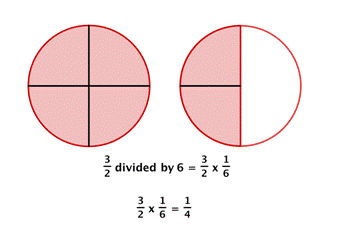
Each person gets one piece, so each person gets [latex]\dfrac{1}{4}[/latex] of a pizza.
Dividing a fraction by a whole number is the same as multiplying by the reciprocal, so you can always use multiplication of fractions to solve division problems.
Example
Find [latex]\dfrac{2}{3}\div \normalsize 4[/latex]
The same idea will work when the divisor (the number being divided) is a fraction.
Divide a Whole Number by a Fraction
Let’s use money to model [latex]2\div\Large\frac{1}{4}[/latex]. We often read [latex]\Large\frac{1}{4}[/latex] as a ‘quarter’, and we know that a quarter is one-fourth of a dollar as shown in the image below. So we can think of [latex]2\div\Large\frac{1}{4}[/latex] as, “How many quarters are there in two dollars?” One dollar is [latex]4[/latex] quarters, so [latex]2[/latex] dollars would be [latex]8[/latex] quarters. So again, [latex]2\div\dfrac{1}{4}=\dfrac{2}{1}\cdot\dfrac{4}{1}=8[/latex].
The U.S. coin called a quarter is worth one-fourth of a dollar.

Let’s look at another way to model [latex]2\div\Large\frac{1}{4}[/latex].
Example
Divide: [latex]2\div\Large\frac{1}{4}[/latex]
Try It
Divide: [latex]2\div\Large\frac{1}{3}[/latex]
Divide: [latex]3\div\Large\frac{1}{2}[/latex]
Try It
The next video shows more examples of how to divide a whole number by a fraction.
Example
Divide. [latex]9\div\dfrac{1}{2}[/latex]
Divide a Fraction by a Fraction
Sometimes you need to solve a problem that requires dividing a fraction by a fraction. Suppose we want to find the quotient: [latex]\Large\frac{1}{2}\normalsize\div\Large\frac{1}{6}[/latex]. We need to figure out how many [latex]\Large\frac{1}{6}\normalsize\text{s}[/latex] there are in [latex]\Large\frac{1}{2}[/latex]. We can use fraction tiles to model this division. We start by lining up the half and sixth fraction tiles as shown below. Notice, there are three [latex]\Large\frac{1}{6}[/latex] tiles in [latex]\Large\frac{1}{2}[/latex], so [latex]\Large\frac{1}{2}\normalsize\div\Large\frac{1}{6}\normalsize=3[/latex].

Example
Model: [latex]\Large\frac{1}{4}\normalsize\div\Large\frac{1}{8}[/latex]
Solution:
We want to determine how many [latex]\Large\frac{1}{8}\normalsize\text{s}[/latex] are in [latex]\Large\frac{1}{4}[/latex]. Start with one [latex]\Large\frac{1}{4}[/latex] tile. Line up [latex]\Large\frac{1}{8}[/latex] tiles underneath the [latex]\Large\frac{1}{4}[/latex] tile.

There are two [latex]\Large\frac{1}{8}[/latex]s in [latex]\Large\frac{1}{4}[/latex].
So, [latex]\Large\frac{1}{4}\normalsize\div\Large\frac{1}{8}\normalsize=2[/latex].
Try It
Model: [latex]\Large\frac{1}{3}\normalsize\div\Large\frac{1}{6}[/latex]
Model: [latex]\Large\frac{1}{2}\normalsize\div\Large\frac{1}{4}[/latex]
The following video shows another way to model division of two fractions.
Using fraction tiles, we showed that [latex]\Large\frac{1}{2}\normalsize\div\Large\frac{1}{6}\normalsize=3[/latex]. Notice that [latex]\Large\frac{1}{2}\cdot \frac{6}{1}\normalsize=3[/latex] also. How are [latex]\Large\frac{1}{6}[/latex] and [latex]\Large\frac{6}{1}[/latex] related? They are reciprocals. This leads us to the procedure for fraction division. Suppose you have a pizza that is already cut into [latex]4[/latex] slices. How many [latex]\dfrac{1}{2}[/latex] slices are there?
 |
 |
There are [latex]8[/latex] slices. You can see that dividing [latex]4[/latex] by [latex]\dfrac{1}{2}[/latex] gives the same result as multiplying [latex]4[/latex] by [latex]2[/latex].
What would happen if you needed to divide each slice into thirds?
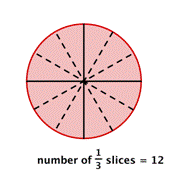
You would have [latex]12[/latex] slices, which is the same as multiplying [latex]4[/latex] by [latex]3[/latex].
Fraction Division
If [latex]a,b,c,\text{ and }d[/latex] are numbers where [latex]b\ne 0,c\ne 0,\text{ and }d\ne 0[/latex], then
[latex]\Large\frac{a}{b}\normalsize\div\Large\frac{c}{d}=\frac{a}{b}\cdot \frac{d}{c}[/latex]
To divide fractions, multiply the first fraction by the reciprocal of the second.
We need to say [latex]b\ne 0,c\ne 0\text{ and }d\ne 0[/latex] to be sure we don’t divide by zero.
Tip: Here’s a rhyme to help you with dividing fractions. When dividing fractions don’t ask why, just flip the second and multiply.
Dividing with Fractions
- Find the reciprocal of the divisor (the number that follows the division symbol).
- Multiply the dividend (the number before the division symbol) by the reciprocal of the divisor (the number after the division symbol).
Any easy way to remember how to divide fractions is the phrase “keep, change, flip.” This means to KEEP the first number, CHANGE the division sign to multiplication, and then FLIP (use the reciprocal) of the second number.
Example
Divide [latex]\dfrac{2}{3}\div\dfrac{1}{6}[/latex]
Example
Divide [latex]\dfrac{3}{5}\div\dfrac{2}{3}[/latex]
Watch this video for more examples of dividing fractions using a reciprocal.
When solving a division problem by multiplying by the reciprocal, remember to write all whole numbers and mixed numbers as improper fractions before doing calculations [latex](\text{i.e. } 5=\dfrac{5}{1}[/latex] and [latex]1\dfrac{3}{4}=\dfrac{7}{4})[/latex]. You can review how to convert mixed numbers to improper fractions here. The final answer should always be simplified and written as a mixed number if larger than [latex]1[/latex].
Try It
Example
Divide, and write the answer in simplified form: [latex]\Large\frac{2}{5}\normalsize\div\Large\left(-\frac{3}{7}\right)[/latex]
Example
Divide, and write the answer in simplified form: [latex]\Large-\frac{3}{4}\normalsize\div\Large\left(-\frac{7}{8}\right)[/latex]
Try It
The following video shows more examples of dividing fractions that are negative.
Example
Divide, and write the answer in simplified form: [latex]\Large\frac{2}{3}\normalsize\div\Large\frac{n}{5}[/latex]
Try It
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Ex 1: Divide Fractions (Basic). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/F5YSNLel3n8. License: CC BY: Attribution
- College Algebra. Provided by: OpenStax. Located at: http://cnx.org/contents/yqV9q0HH@7.3:s7ku6WX5@2/Multiply-and-Divide-Fractions. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@7.3





