Learning Outcomes
- Draw the graph of a line using slope and a point on the line
- Write the equation of a line using slope and y-intercept
When graphing a line we found one method we could use is to make a table of values. We also learned how to graph lines by plotting points, by using intercepts, and by recognizing horizontal and vertical lines. However, if we can identify some properties of the line, we may be able to make a graph much quicker and easier.
Graphing a Line Using Slope and a Point on the Line
Another method we can use to graph lines is the point-slope method. Sometimes, we will be given one point and the slope of the line, instead of its equation. When this happens, we use the definition of slope to draw the graph of the line.
example
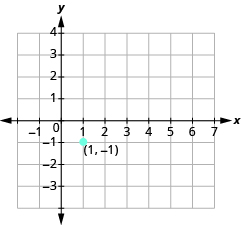
Graph the line passing through the point [latex]\left(1,-1\right)[/latex] whose slope is [latex]m=\Large\frac{3}{4}[/latex].
Solution
Plot the given point, [latex]\left(1,-1\right)[/latex].
Use the slope formula [latex]m=\Large\frac{\text{rise}}{\text{run}}[/latex] to identify the rise and the run.
[latex]\begin{array}{}\\ \\ m=\frac{3}{4}\hfill \\ \frac{\text{rise}}{\text{run}}=\frac{3}{4}\hfill \\ \\ \\ \text{rise}=3\hfill \\ \text{run}=4\hfill \end{array}[/latex]
Starting at the point we plotted, count out the rise and run to mark the second point. We count [latex]3[/latex] units up and [latex]4[/latex] units right.
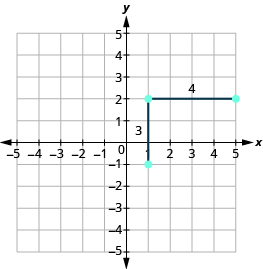
Then we connect the points with a line and draw arrows at the ends to show it continues.
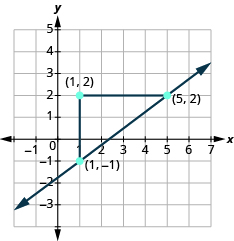
We can check our line by starting at any point and counting up [latex]3[/latex] and to the right [latex]4[/latex]. We should get to another point on the line.
try it
Graph a line given a point and a slope
-
- Plot the given point.
- Use the slope formula to identify the rise and the run.
- Starting at the given point, count out the rise and run to mark the second point.
- Connect the points with a line.
example
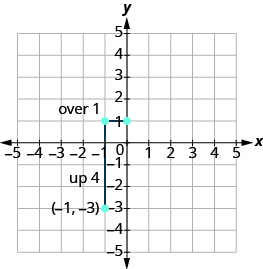
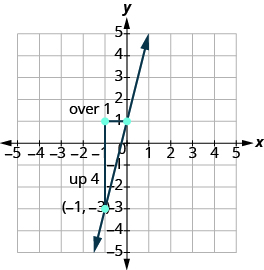
Graph the line passing through the point [latex]\left(-1,-3\right)[/latex] whose slope is [latex]m=4[/latex]
try it
You can watch the video below for another example of how to graph a line given a point and a slope.
A special case for graphing using the point-slope method is when the given point is the y-intercept. We will give some examples here and then we will show below why this case is so important.
example
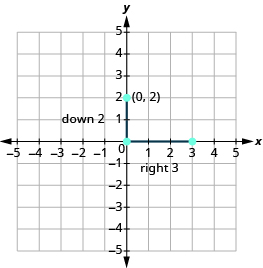
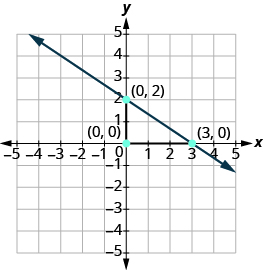
Graph the line with [latex]y[/latex] -intercept [latex]\left(0,2\right)[/latex] and slope [latex]m=-\Large\frac{2}{3}[/latex]
try it
Slope-Intercept Form
We will now show you what is so special about the case in which the given point is the y-intercept. The slope can be represented by m and the y-intercept, where it crosses the axis and [latex]x=0[/latex], can be represented by [latex](0,b)[/latex] where b is the value where the graph crosses the vertical y-axis. Any other point on the line can be represented by [latex](x,y)[/latex].
Slope-Intercept Form of a Linear Equation
In the equation [latex]y=mx+b[/latex],
- m is the slope of the graph.
- b is the y value of the y-intercept of the graph.
This formula is known as the slope-intercept equation. If we know the slope and the y-intercept we can easily find the equation that represents the line.
Example
Write the equation of the line that has a slope of [latex] \displaystyle \frac{1}{2}[/latex] and a y-intercept of [latex]−5[/latex].
We can also easily find the equation by looking at a graph and finding the slope and y-intercept.
Example
Write the equation of the line in the graph by identifying the slope and y-intercept.
![]()
We can also move in the opposite direction. When we are given an equation in the slope-intercept form of [latex]y=mx+b[/latex], we can easily identify the slope and y-intercept and graph the equation from this information. When we have an equation in slope-intercept form we can graph it by first plotting the y-intercept, then using the slope, find a second point and connecting the dots.
Example
Graph [latex]y=\frac{1}{2}x-4[/latex] using the slope-intercept equation.
(NOTE: it is important for the equation to first be in slope intercept form. If it is not, we will have to solve it for [latex]y[/latex] so we can identify the slope and the [latex]y[/latex]-intercept.)
Try It
You can watch the video below for another example of how to write the equation of the line, when given a graph, by identifying the slope and y-intercept.