Learning Outcomes
- Evaluate exponential expressions
Repeated Image
Anatomy of exponential terms
We use exponential notation to write repeated multiplication of the same quantity. For example, [latex]{2}^{4}[/latex] means to multiply four factors of [latex]2[/latex], so [latex]{2}^{4}[/latex] means [latex]2\cdot 2\cdot 2\cdot 2[/latex]. Conversely, [latex]10\cdot10\cdot10[/latex] can be written more succinctly as [latex]10^{3}[/latex]. The [latex]10[/latex] in [latex]10^{3}[/latex] is called the base. The [latex]3[/latex] in [latex]10^{3}[/latex] is called the exponent. The expression [latex]10^{3}[/latex] is called the exponential expression. Knowing the names for the parts of an exponential expression or term will help you learn how to perform mathematical operations on them.
Exponential Notation
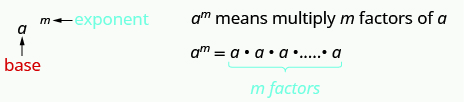
This is read [latex]a[/latex] to the [latex]{m}^{\mathrm{th}}[/latex] power.
In the expression [latex]{a}^{m}[/latex], the exponent tells us how many times we use the base [latex]a[/latex] as a factor.
[latex]10^{3}[/latex] is read as “[latex]10[/latex] to the third power” or “[latex]10[/latex] cubed.” It means [latex]10\cdot10\cdot10[/latex], or [latex]1,000[/latex].
[latex]8^{2}[/latex] is read as “[latex]8[/latex] to the second power” or “[latex]8[/latex] squared.” It means [latex]8\cdot8[/latex], or [latex]64[/latex].
[latex]5^{4}[/latex] is read as “[latex]5[/latex] to the fourth power.” It means [latex]5\cdot5\cdot5\cdot5[/latex], or [latex]625[/latex].
[latex]b^{5}[/latex] is read as “b to the fifth power.” It means [latex]{b}\cdot{b}\cdot{b}\cdot{b}\cdot{b}[/latex]. Its value will depend on the value of b.
The exponent applies only to the number that it is next to. Therefore, in the expression [latex]xy^{4}[/latex], only the [latex]y[/latex] is affected by the [latex]4[/latex]. [latex]xy^{4}[/latex] means [latex]{x}\cdot{y}\cdot{y}\cdot{y}\cdot{y}[/latex].
If the exponential expression is negative, such as [latex]−3^{4}[/latex], it means [latex]–\left(3\cdot3\cdot3\cdot3\right)[/latex] or [latex]−81[/latex].
If [latex]−3[/latex] is to be the base, it must be written as [latex]\left(−3\right)^{4}[/latex], which means [latex]−3\cdot−3\cdot−3\cdot−3[/latex], or [latex]81[/latex].
Likewise, [latex]\left(−x\right)^{4}=\left(−x\right)\cdot\left(−x\right)\cdot\left(−x\right)\cdot\left(−x\right)=x^{4}[/latex], while [latex]−x^{4}=–\left(x\cdot x\cdot x\cdot x\right)[/latex].
You can see that there is quite a difference, so you have to be very careful! The following examples show how to identify the base and the exponent, as well as how to identify the expanded and exponential format of writing repeated multiplication.
Example
Identify the exponent and the base in the following terms, then simplify:
- [latex]7^{2}[/latex]
- [latex]{\left(\frac{1}{2}\right)}^{3}[/latex]
- [latex]2x^{3}[/latex]
- [latex]\left(-5\right)^{2}[/latex]
In the following video you are provided more examples of applying exponents to various bases.
Before we begin working with variable expressions containing exponents, let’s simplify a few expressions involving only numbers.
example
Simplify:
1. [latex]{5}^{3}[/latex]
2. [latex]{9}^{1}[/latex]
Solution
| 1. | |
| [latex]{5}^{3}[/latex] | |
| Multiply [latex]3[/latex] factors of [latex]5[/latex]. | [latex]5\cdot 5\cdot 5[/latex] |
| Simplify. | [latex]125[/latex] |
| 2. | |
| [latex]{9}^{1}[/latex] | |
| Multiply [latex]1[/latex] factor of [latex]9[/latex]. | [latex]9[/latex] |
try it
example
Simplify:
1. [latex]{\left({\Large\frac{7}{8}}\right)}^{2}[/latex]
2. [latex]{\left(0.74\right)}^{2}[/latex]
try it
example
Simplify:
1. [latex]{\left(-3\right)}^{4}[/latex]
2. [latex]{-3}^{4}[/latex]
try it
Evaluate expressions
Evaluating expressions containing exponents is the same as evaluating the linear expressions from earlier in the course. You substitute the value of the variable into the expression and simplify.
You can use the order of operations to evaluate the expressions containing exponents. First, evaluate anything in Parentheses or grouping symbols. Next, look for Exponents, followed by Multiplication and Division (reading from left to right), and lastly, Addition and Subtraction (again, reading from left to right).
So, when you evaluate the expression [latex]5x^{3}[/latex] if [latex]x=4[/latex], first substitute the value [latex]4[/latex] for the variable [latex]x[/latex]. Then evaluate, using order of operations.
Example
Evaluate [latex]5x^{3}[/latex] if [latex]x=4[/latex].
In the example below, notice how adding parentheses can change the outcome when you are simplifying terms with exponents.
Example
Evaluate [latex]\left(5x\right)^{3}[/latex] if [latex]x=4[/latex].
The addition of parentheses made quite a difference! Parentheses allow you to apply an exponent to variables or numbers that are multiplied, divided, added, or subtracted to each other.
Try It
Example
Evaluate [latex]x^{3}[/latex] if [latex]x=−4[/latex].
Caution! Whether to include a negative sign as part of a base or not often leads to confusion. To clarify whether a negative sign is applied before or after the exponent, here is an example.
What is the difference in the way you would evaluate these two terms?
- [latex]-{3}^{2}[/latex]
- [latex]{\left(-3\right)}^{2}[/latex]
To evaluate 1), you would apply the exponent to the three first, then apply the negative sign last, like this:
[latex]\begin{array}{c}-\left({3}^{2}\right)\\=-\left(9\right) = -9\end{array}[/latex]
To evaluate 2), you would apply the exponent to the [latex]3[/latex] and the negative sign:
[latex]\begin{array}{c}{\left(-3\right)}^{2}\\=\left(-3\right)\cdot\left(-3\right)\\={ 9}\end{array}[/latex]
The key to remembering this is to follow the order of operations. The first expression does not include parentheses so you would apply the exponent to the integer [latex]3[/latex] first, then apply the negative sign. The second expression includes parentheses, so hopefully you will remember that the negative sign also gets squared.
In the next sections, you will learn how to simplify expressions that contain exponents. Come back to this page if you forget how to apply the order of operations to a term with exponents, or forget which is the base and which is the exponent!
In the following video you are provided with examples of evaluating exponential expressions for a given number.
