Learning Outcomes
- Simplify expressions using the distributive property
Simplify Expressions Using the Distributive Property
Suppose three friends are going to the movies. They each need [latex]$9.25[/latex]; that is, [latex]9[/latex] dollars and [latex]1[/latex] quarter. How much money do they need all together? You can think about the dollars separately from the quarters.


They need [latex]3[/latex] times [latex]$9[/latex], so [latex]$27[/latex], and [latex]3[/latex] times [latex]1[/latex] quarter, so [latex]75[/latex] cents. In total, they need [latex]$27.75[/latex].
If you think about doing the math in this way, you are using the Distributive Property.
Distributive Property
If [latex]a,b,c[/latex] are real numbers, then
[latex]a\left(b+c\right)=ab+ac[/latex]
Back to our friends at the movies, we could show the math steps we take to find the total amount of money they need like this:
[latex]3(9.25)\\3(9\quad+\quad0.25)\\3(9)\quad+\quad3(0.25)\\27\quad+\quad0.75\\27.75[/latex]
In algebra, we use the Distributive Property to remove parentheses as we simplify expressions. For example, if we are asked to simplify the expression [latex]3\left(x+4\right)[/latex], the order of operations says to work in the parentheses first. But we cannot add [latex]x[/latex] and [latex]4[/latex], since they are not like terms (Go here for a review on adding like terms). So we use the Distributive Property, as shown in the next example.
example
Simplify: [latex]3\left(x+4\right)[/latex]
Solution:
| [latex]3\left(x+4\right)[/latex] | |
| Distribute. | [latex]3\cdot x+3\cdot 4[/latex] |
| Multiply. | [latex]3x+12[/latex] |
Some students find it helpful to draw in arrows to remind them how to use the Distributive Property. Then the first step in the previous example would look like this:
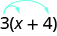
[latex]3\cdot x+3\cdot 4[/latex]
Now you try.
try it
In our next example, there is a coefficient on the variable y. When you use the distributive property, you multiply the two numbers together, just like simplifying any product. You will also see another example where the expression in parentheses is subtraction, rather than addition. You will need to be careful to change the sign of your product.
example
Simplify: [latex]6\left(5y+1\right)[/latex]
Simplify: [latex]2\left(x - 3\right)[/latex]
Now you try.
try it
The distributive property can be used to simplify expressions that look slightly different from [latex]a\left(b+c\right)[/latex]. Here are two other forms.
different Forms of the Distributive Property
If [latex]a,b,c[/latex] are real numbers, then
[latex]a\left(b+c\right)=ab+ac[/latex]
Other forms
[latex]a\left(b-c\right)=ab-ac[/latex]
[latex]\left(b+c\right)a=ba+ca[/latex]
In the following video we show more examples of using the distributive property.
Using the Distributive Property With Fractions and Decimals
Do you remember how to multiply a fraction by a whole number? We’ll need to do that in the next two examples. The distributive property comes in all shapes and sizes, and can include fractions or decimals as well.
example
Simplify: [latex]\Large\frac{3}{4}\normalsize\left(n+12\right)[/latex]
Simplify: [latex]8\Large\left(\frac{3}{8}\normalsize x+\Large\frac{1}{4}\right)[/latex].
Now you try.
try it
Using the Distributive Property as shown in the next example will be very useful when we solve money applications later.
example
Simplify: [latex]100\left(0.3+0.25q\right)[/latex]
Now you try.
try it
Distributing a Variable
In the next example we’ll multiply by a variable. We’ll need to do this in a later chapter.
example
Simplify: [latex]m\left(n - 4\right)[/latex]
Now you try.
try it
The Backwards Form of the Distributive Property
The next example will use the ‘backwards’ form of the Distributive Property, [latex]\left(b+c\right)a=ba+ca[/latex].
example
Simplify: [latex]\left(x+8\right)p[/latex]
try it
Distributing a Negative Term
When you distribute a negative number, you need to be extra careful to get the signs correct.
example
Simplify: [latex]-2\left(4y+1\right)[/latex]
Simplify: [latex]-11\left(4 - 3a\right)[/latex]
try it
In the next example, we will show how to use the Distributive Property to find the opposite of an expression. Remember, [latex]-a=-1\cdot a[/latex].
example
Simplify: [latex]-\left(y+5\right)[/latex]


