Key Concepts
- Real numbers
The Order of Operations
- Perform all operations within grouping symbols first. Grouping symbols include parentheses ( ), brackets [ ], braces { }, and fraction bars.
- Evaluate exponents or square roots.
- Multiply or divide, from left to right.
- Add or subtract, from left to right.
This order of operations is true for all real numbers.
Glossary:
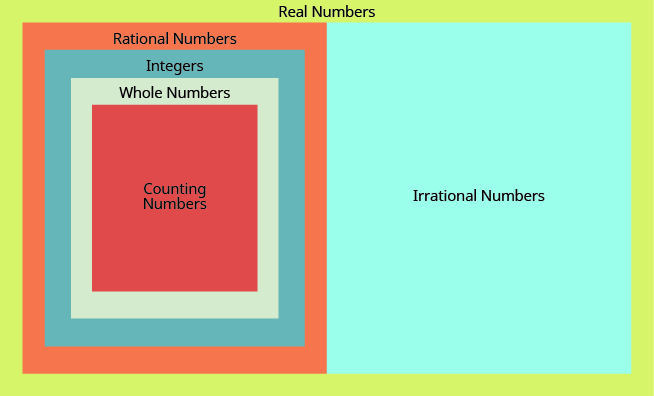
- Irrational number
- A number that cannot be written as the ratio of two integers. Its decimal form does not stop and does not repeat.
- Rational number
- A number that can be written in the form [latex]{\Large\frac{p}{q}}[/latex] , where p and q are integers and [latex]q\ne 0[/latex] . Its decimal form stops or repeats.
- Real number:
- A number that is either rational or irrational.
Contribute!
Did you have an idea for improving this content? We’d love your input.
