Translating Words to Equations and Solving

Learning Outcomes

  • Translate statements into equations and solve

Translate Sentences to Equations and Solve

Recall the four properties of equality—subtraction, addition, division, and multiplication. We’ll list them all together here for easy reference. We will use these to solve equations that contain fractions.

Subtraction Property of Equality:

For any real numbers [latex]\mathit{\text{a, b,}}[/latex] and [latex]\mathit{\text{c,}}[/latex]

if [latex]a=b[/latex], then [latex]a-c=b-c[/latex].

 Addition Property of Equality:

For any real numbers [latex]\mathit{\text{a, b,}}[/latex] and [latex]\mathit{\text{c,}}[/latex]

if [latex]a=b[/latex], then [latex]a+c=b+c[/latex].
Division Property of Equality:

For any numbers [latex]\mathit{\text{a, b,}}[/latex] and [latex]\mathit{\text{c,}}[/latex] where [latex]\mathit{\text{c}}\ne \mathit{0}[/latex]

if [latex]a=b[/latex], then [latex]\Large\frac{a}{c}= \Large\frac{b}{c}[/latex]

 Multiplication Property of Equality:

For any real numbers [latex]\mathit{\text{a, b,}}[/latex] and [latex]\mathit{\text{c}}[/latex]

if [latex]a=b[/latex], then [latex]ac=bc[/latex]

When you add, subtract, multiply or divide the same quantity from both sides of an equation, you still have equality.

In the next few examples, we’ll translate sentences that contain fractions into equations and then solve the equations.  When we translate sentences into equations, we start by locating the “equals” word or words and translating them into an equals sign.  (Note: This could be the phrase “is equal to” or simply the word “is”).  We then translate the words to the left of the “equals” word(s) into an algebraic expression and the words to the right of the “equals” word(s) into an algebraic expression.

In the next examples we will use the Multiplication Property of Equality to solve the equation.

Example

Translate and solve: [latex]n[/latex] divided by [latex]6[/latex] is [latex]-24[/latex].

Solution:

Translate. .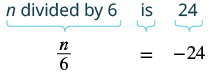
Multiply both sides by [latex]6[/latex] . [latex]\color{red}{6}\cdot\Large\frac{n}{6}\normalsize=\color{red}{6}(-24)[/latex]
Simplify. [latex]n=-144[/latex]
Check: Is [latex]-144[/latex] divided by [latex]6[/latex] equal to [latex]-24[/latex] ?
Translate. [latex]\Large\frac{-144}{6}\normalsize\stackrel{?}{=}-24[/latex]
Simplify. It checks. [latex]-24=-24\quad\checkmark[/latex]

Try It

Example

Translate and solve: The quotient of [latex]q[/latex] and [latex]-5[/latex] is [latex]70[/latex].

Try It

Example

Translate and solve: Two-thirds of [latex]f[/latex] is [latex]18[/latex].

try It

Example

Translate and solve: The quotient of [latex]m[/latex] and [latex]\Large\frac{5}{6}[/latex] is [latex]\Large\frac{3}{4}[/latex].

Try It

In the next set of examples, we will use the Subtraction and Addition Properties of Equality to solve the equations.

Example

Translate and solve: The sum of three-eighths and [latex]x[/latex] is three and one-half.

try It