Learning Outcomes
- Use the definition of percent
- Identify the amount, the base, and the percent in a percent problem
- Find the unknown in a percent problem
Percents are used in many different applications. Percents are used widely to describe how something changed. For example, you may have heard that the amount of rainfall this month had decreased by [latex]12\%[/latex] from last year, or that the number of jobless claims has increase by [latex]5\%[/latex] this quarter over last quarter.
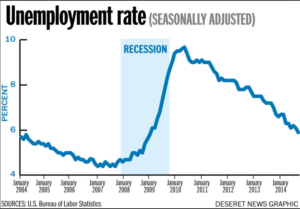
Unemployment rate as percent by year between 2004 and 2014.
We regularly use this kind of language to quickly describe how much something increased or decreased over time or between significant events.
How many cents are in one dollar? There are [latex]100[/latex] cents in a dollar. How many years are in a century? There are [latex]100[/latex] years in a century. Does this give you a clue about what the word “percent” means? It is really two words, “per cent,” and means per one hundred. A percent is a ratio whose denominator is [latex]100[/latex]. We use the percent symbol [latex]\text{%,}[/latex] to show percent.
Percent
A percent is a ratio whose denominator is [latex]100[/latex].
According to data from the American Association of Community Colleges [latex]\left(2015\right)[/latex], about [latex]\text{57%}[/latex] of community college students are female. This means [latex]57[/latex] out of every [latex]100[/latex] community college students are female, as the image below shows. Out of the [latex]100[/latex] squares on the grid, [latex]57[/latex] are shaded, which we write as the ratio [latex]\Large\frac{57}{100}[/latex].
Among every [latex]100[/latex] community college students, [latex]57[/latex] are female.
Similarly, [latex]\text{25%}[/latex] means a ratio of [latex]\Large\frac{25}{100}\normalsize ,\text{3%}[/latex] means a ratio of [latex]\Large\frac{3}{100}[/latex] and [latex]\text{100%}[/latex] means a ratio of [latex]\Large\frac{100}{100}[/latex]. In words, “one hundred percent” means the total [latex]\text{100%}[/latex] is [latex]\Large\frac{100}{100}[/latex], and since [latex]\Large\frac{100}{100}\normalsize =1[/latex], we see that [latex]\text{100%}[/latex] means [latex]1[/latex] whole.
example
According to the Public Policy Institute of California [latex]\left(2010\right)\text{, }\text{44%}[/latex] of parents of public school children would like their youngest child to earn a graduate degree. Write this percent as a ratio.
Solution
| The amount we want to convert is [latex]44%[/latex]. | [latex]44%[/latex] |
| Write the percent as a ratio. Remember that percent means per [latex]100[/latex]. | [latex]\Large\frac{44}{100}[/latex] |
Try it
example
In [latex]2007[/latex], according to a U.S. Department of Education report, [latex]21[/latex] out of every [latex]100[/latex] first-time freshmen college students at [latex]\text{4-year}[/latex] public institutions took at least one remedial course. Write this as a ratio and then as a percent.
try it
From the previous example, we can identify three important parts to finding the percent of a whole:
- the percent, has the percent symbol (%) or the word “percent”
- the amount, the amount is part of the whole
- and the base, the base is the whole amount
The following examples show how to identify the three parts: the percent, the base, and the amount.
Example
Identify the percent, amount, and base in this problem.
[latex]30[/latex] is [latex]20\%[/latex] of what number?
The previous problem states that [latex]30[/latex] is a portion of another number. That means [latex]30[/latex] is the amount. Note that this problem could be rewritten: [latex]20\%[/latex] of what number is [latex]30[/latex]?
Example
Identify the percent, amount, and base in this problem.
What percent of [latex]30[/latex] is [latex]3[/latex]?
Example
Identify the percent, amount, and base in this problem.
What is [latex]60\%[/latex] of [latex]45[/latex]?
Try it
The following video provides more examples that describe how to identify the percent, amount, and base in a percent problem.
