Learning Outcomes
- Find the supplement of an angle
- Find the complement of an angle
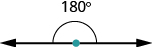
Are you familiar with the phrase ‘do a [latex]180[/latex]?’ It means to make a full turn so that you face the opposite direction. It comes from the fact that the measure of an angle that makes a straight line is [latex]180[/latex] degrees. See the image below.
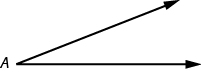
An angle is formed by two rays that share a common endpoint. Each ray is called a side of the angle and the common endpoint is called the vertex. An angle is named by its vertex. In the image below, [latex]\angle A[/latex] is the angle with vertex at point [latex]A[/latex]. The measure of [latex]\angle A[/latex] is written [latex]m\angle A[/latex].
[latex]\angle A[/latex] is the angle with vertex at [latex]\text{point }A[/latex].
We measure angles in degrees, and use the symbol [latex]^ \circ[/latex] to represent degrees. We use the abbreviation [latex]m[/latex] to for the measure of an angle. So if [latex]\angle A[/latex] is [latex]\text{27}^ \circ[/latex], we would write [latex]m\angle A=27^ \circ[/latex].
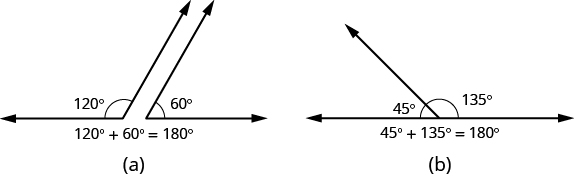
If the sum of the measures of two angles is [latex]\text{180}^ \circ[/latex], then they are called supplementary angles. In the images below, each pair of angles is supplementary because their measures add to [latex]\text{180}^ \circ[/latex]. Each angle is the supplement of the other.
The sum of the measures of supplementary angles is [latex]\text{180}^ \circ[/latex].
If the sum of the measures of two angles is [latex]\text{90}^ \circ[/latex], then the angles are complementary angles. In the images below, each pair of angles is complementary, because their measures add to [latex]\text{90}^ \circ[/latex]. Each angle is the complement of the other.
The sum of the measures of complementary angles is [latex]\text{90}^ \circ[/latex].
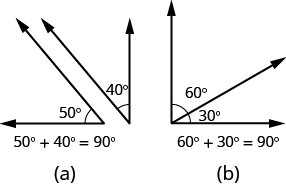
Supplementary and Complementary Angles
If the sum of the measures of two angles is [latex]\text{180}^\circ[/latex], then the angles are supplementary.
If angle [latex]A[/latex] and angle [latex]B[/latex] are supplementary, then [latex]m\angle{A}+m\angle{B}=180^\circ[/latex].
If the sum of the measures of two angles is [latex]\text{90}^\circ[/latex], then the angles are complementary.
If angle [latex]A[/latex] and angle [latex]B[/latex] are complementary, then [latex]m\angle{A}+m\angle{B}=90^\circ[/latex].
In this section and the next, you will be introduced to some common geometry formulas. We will adapt our Problem Solving Strategy for Geometry Applications. The geometry formula will name the variables and give us the equation to solve.
In addition, since these applications will all involve geometric shapes, it will be helpful to draw a figure and then label it with the information from the problem. We will include this step in the Problem Solving Strategy for Geometry Applications.
Use a Problem Solving Strategy for Geometry Applications.
- Read the problem and make sure you understand all the words and ideas. Draw a figure and label it with the given information.
- Identify what you are looking for.
- Name what you are looking for and choose a variable to represent it.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
The next example will show how you can use the Problem Solving Strategy for Geometry Applications to answer questions about supplementary and complementary angles.
example
An angle measures [latex]\text{40}^ \circ[/latex].
1. Find its supplement
2. Find its complement
Solution
| 1. | |
| Step 1. Read the problem. Draw the figure and label it with the given information. | 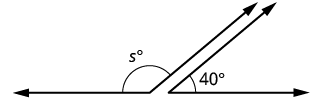 |
| Step 2. Identify what you are looking for. | The supplement of a [latex]40°[/latex]angle. |
| Step 3. Name. Choose a variable to represent it. | Let [latex]s=[/latex]the measure of the supplement. |
| Step 4. Translate.
Write the appropriate formula for the situation and substitute in the given information. |
[latex]m\angle A+m\angle B=180°[/latex]
[latex]s+40°=180°[/latex] |
| Step 5. Solve the equation. | [latex]s=140°[/latex] |
| Step 6. Check:
[latex]140°+40°\stackrel{?}{=}180°[/latex] [latex]180°=180°\checkmark[/latex] |
|
| Step 7. Answer the question. | The supplement of the [latex]40°[/latex]angle is [latex]140°[/latex]. |
| 2. | ||
| Step 1. Read the problem. Draw the figure and label it with the given information. | 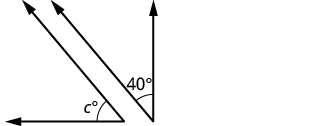 |
|
| Step 2. Identify what you are looking for. |
|
|
| Step 3. Name. Choose a variable to represent it. | Let [latex]c=[/latex]the measure of the complement. | |
| Step 4. Translate.
Write the appropriate formula for the situation and substitute in the given information. |
[latex]m\angle A+m\angle B=90°[/latex] | |
| Step 5. Solve the equation. | [latex]c+40°=90°[/latex]
[latex]c=50°[/latex] |
|
| Step 6. Check:
[latex]50°+40°\stackrel{?}{=}90°[/latex] [latex]90°=90°\quad\checkmark[/latex] |
||
| Step 7. Answer the question. | The complement of the [latex]40°[/latex]angle is [latex]50°[/latex]. |
try it
In the following video we show more examples of how to find the supplement and complement of an angle.
Did you notice that the words complementary and supplementary are in alphabetical order just like [latex]90[/latex] and [latex]180[/latex] are in numerical order?
Exercises
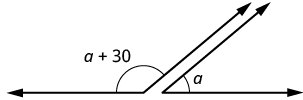
Two angles are supplementary. The larger angle is [latex]\text{30}^ \circ[/latex] more than the smaller angle. Find the measure of both angles.
try it
Candela Citations
- Question ID 146497, 146496, 146495. Authored by: Lumen Learning. License: CC BY: Attribution
- Determine the Complement and Supplement of a Given Angle. Authored by: James Sousa (mathispower4u.com). Located at: https://youtu.be/ZQ_L3yJOfqM. License: CC BY: Attribution
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@9.757