Learning Outcomes
- Find the circumference and area of a circular object given its radius or diameter
- Calculate the diameter or radius of a circular object given its circumference
In a previous section, we learned the properties of circles. We’ll show them here again to refer to as we use them to solve applications.
Properties of Circles
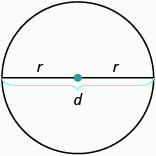
- [latex]r[/latex] is the length of the radius
- [latex]d[/latex] is the length of the diameter
- [latex]d=2r[/latex]
- Circumference is the perimeter of a circle. The formula for circumference is [latex]C=2\pi r[/latex]
- The formula for area of a circle is [latex]A=\pi {r}^{2}[/latex]
Remember that we approximate [latex]\pi [/latex] with [latex]3.14[/latex] or [latex]\Large\frac{22}{7}[/latex] depending on whether the radius of the circle is given as a decimal or a fraction. If you use the [latex]\pi [/latex] key on your calculator to do the calculations in this section, your answers will be slightly different from the answers shown. That is because the [latex]\pi [/latex] key uses more than two decimal places.
example
A circular sandbox has a radius of [latex]2.5[/latex] feet. Find 1. the circumference and 2. the area of the sandbox.
Solution
| 1.
Step 1. Read the problem. Draw the figure and label it with the given information. |
 |
| Step 2. Identify what you are looking for. | The circumference of the circle |
| Step 3. Name. Choose a variable to represent it. | Let c = circumference of the circle |
| Step 4. Translate.
Write the appropriate formula Substitute |
[latex]C=2\pi r[/latex]
[latex]C=2\pi \left(2.5\right)[/latex] |
| Step 5. Solve the equation. | [latex]C\approx 2\left(3.14\right)\left(2.5\right)[/latex]
[latex]C\approx 15\text{ft}[/latex] |
| Step 6. Check. Does this answer make sense?
Yes. If we draw a square around the circle, its sides would be [latex]5[/latex] ft (twice the radius), so its perimeter would be [latex]20[/latex] ft. This is slightly more than the circle’s circumference, [latex]15.7[/latex] ft.
|
|
| Step 7. Answer the question. | The circumference of the sandbox is [latex]15.7[/latex] feet. |
| 2.
Step 1. Read the problem. Draw the figure and label it with the given information. |
 |
| Step 2. Identify what you are looking for. | The area of the circle |
| Step 3. Name. Choose a variable to represent it. | Let A = the area of the circle |
| Step 4. Translate.
Write the appropriate formula Substitute |
[latex]A=\pi {r}^{2}[/latex]
[latex]A=\pi{\left(2.5\right)}^{2}[/latex] |
| Step 5. Solve the equation. | [latex]A\approx \left(3.14\right){\left(2.5\right)}^{2}[/latex]
[latex]A\approx 19.625\text{sq. ft}[/latex] |
| Step 6. Check.
Yes. If we draw a square around the circle, its sides would be [latex]5[/latex] ft, as shown in part ⓐ. So the area of the square would be [latex]25[/latex] sq. ft. This is slightly more than the circle’s area, [latex]19.625[/latex] sq. ft. |
|
| Step 7. Answer the question. | The area of the circle is [latex]19.625[/latex] square feet. |
try it
in the following video we show another example of how to find the area of a circle.
We usually see the formula for circumference in terms of the radius [latex]r[/latex] of the circle:
[latex]C=2\pi r[/latex]
But since the diameter of a circle is two times the radius, we could write the formula for the circumference in terms [latex]\text{of }d[/latex].
[latex]\begin{array}{cccc}& & & C=2\pi r\hfill \\ \text{Using the commutative property, we get}\hfill & & & C=\pi \cdot 2r\hfill \\ \text{Then substituting }d=2r\hfill & & & C=\pi \cdot d\hfill \\ \text{So}\hfill & & & C=\pi d\hfill \end{array}[/latex]
We will use this form of the circumference when we’re given the length of the diameter instead of the radius.
example
A circular table has a diameter of four feet. What is the circumference of the table?
try it
In the next video we show two more examples of how to find the circumference of a circle given its diameter, or its radius.
example
Find the diameter of a circle with a circumference of [latex]47.1[/latex] centimeters.




