Focus in on a square centimeter of your skin. Look closer. Closer still. If you could look closely enough, you would see hundreds of thousands of microscopic organisms. They are bacteria, and they are not only on your skin, but in your mouth, nose, and even your intestines. In fact, the bacterial cells in your body at any given moment outnumber your own cells. But that is no reason to feel bad about yourself. While some bacteria can cause illness, many are healthy and even essential to the body.

An electron micrograph of E.Coli bacteria. (credit: “Mattosaurus,” Wikimedia Commons)

Bacteria commonly reproduce through a process called binary fission during which one bacterial cell splits into two. When conditions are right, bacteria can reproduce very quickly. Unlike humans and other complex organisms, the time required to form a new generation of bacteria is often a matter of minutes or hours as opposed to days or years.^[1]

For simplicity’s sake, suppose we begin with a culture of one bacterial cell that can divide every hour. The table below shows the number of bacterial cells at the end of each subsequent hour. We see that the single bacterial cell leads to over one thousand bacterial cells in just ten hours! If we were to extrapolate the table to twenty-four hours, we would have over 16 million!

In this module, we will explore exponential functions which can be used for, among other things, modeling growth patterns such as those found in bacteria. We will also investigate logarithmic functions which are closely related to exponential functions. Both types of functions have numerous real-world applications when it comes to modeling and interpreting data.

Evaluating Exponential Functions

India is the second most populous country in the world with a population of about 1.25 billion people in 2013. The population is growing at a rate of about 1.2% each year.^[2] If this rate continues, the population of India will exceed China’s population by the year 2031. When populations grow rapidly, we often say that the growth is “exponential.” To a mathematician, however, the term exponential growth has a very specific meaning. In this section, we will take a look at exponential functions, which model this kind of rapid growth.

The base of an exponential function must be a positive real number other than 1. Why do we limit the base b to positive values? This is done to ensure that the outputs will be real numbers. Observe what happens if the base is not positive:

• Consider a base of –9 and exponent of [latex]\frac{1}{2}[/latex]. Then [latex]f\left(x\right)=f\left(\frac{1}{2}\right)={\left(-9\right)}^{\frac{1}{2}}=\sqrt{-9}[/latex], which is not a real number.

Why do we limit the base to positive values other than 1? This is because a base of 1 results in the constant function. Observe what happens if the base is 1:

• Consider a base of 1. Then [latex]f\left(x\right)={1}^{x}=1[/latex] for any value of x.

To evaluate an exponential function with the form [latex]f\left(x\right)={b}^{x}[/latex], we simply substitute x with the given value, and calculate the resulting power. For example:

Let [latex]f\left(x\right)={2}^{x}[/latex]. What is [latex]f\left(3\right)[/latex]?

[latex]\begin{array}{llllllll}f\left(x\right)\hfill & ={2}^{x}\hfill & \hfill \\ f\left(3\right)\hfill & ={2}^{3}\text{}\hfill & \text{Substitute }x=3. \hfill \\ \hfill & =8\text{}\hfill & \text{Evaluate the power}\text{.}\hfill \end{array}[/latex]

To evaluate an exponential function, it is important to follow the order of operations. For example:

Let [latex]f\left(x\right)=30{\left(2\right)}^{x}[/latex]. What is [latex]f\left(3\right)[/latex]?

[latex]\begin{array}{c}f\left(x\right)\hfill & =30{\left(2\right)}^{x}\hfill & \hfill \\ f\left(3\right)\hfill & =30{\left(2\right)}^{3}\hfill & \text{Substitute }x=3.\hfill \\ \hfill & =30\left(8\right)\text{ }\hfill & \text{Simplify the power first}\text{.}\hfill \\ \hfill & =240\hfill & \text{Multiply}\text{.}\hfill \end{array}[/latex]

Note that if the order of operations were not followed, the result would be incorrect:

[latex]f\left(3\right)=30{\left(2\right)}^{3}\ne {60}^{3}=216,000[/latex]

Because the output of exponential functions increases very rapidly, the term “exponential growth” is often used in everyday language to describe anything that grows or increases rapidly. However, exponential growth can be defined more precisely in a mathematical sense. If the growth rate is proportional to the amount present, the function models exponential growth.

In more general terms, an exponential function consists of a constant base raised to a variable exponent. To differentiate between linear and exponential functions, let’s consider two companies, A and B. Company A has 100 stores and expands by opening 50 new stores a year, so its growth can be represented by the function [latex]A\left(x\right)=100+50x[/latex]. Company B has 100 stores and expands by increasing the number of stores by 50% each year, so its growth can be represented by the function [latex]B\left(x\right)=100{\left(1+0.5\right)}^{x}[/latex].

A few years of growth for these companies are illustrated below.

The graphs comparing the number of stores for each company over a five-year period are shown below. We can see that, with exponential growth, the number of stores increases much more rapidly than with linear growth.

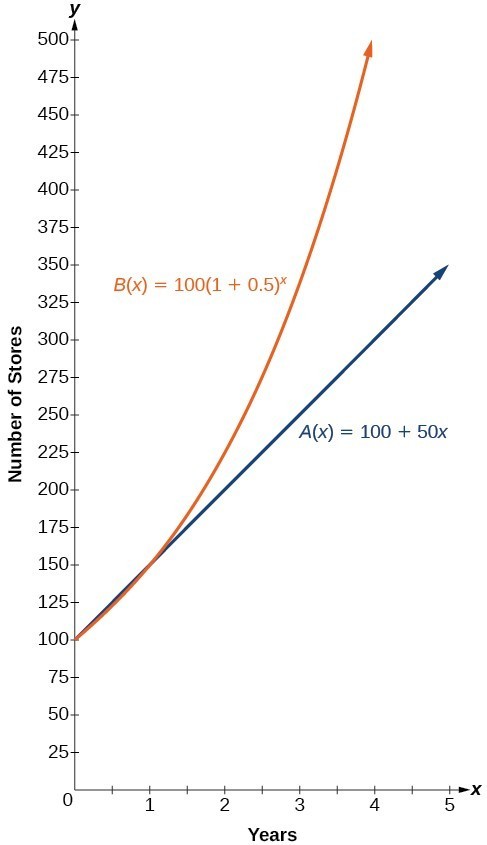
The graph shows the numbers of stores Companies A and B opened over a five-year period.

Notice that the domain for both functions is [latex]\left[0,\infty \right)[/latex], and the range for both functions is [latex]\left[100,\infty \right)[/latex]. After year 1, Company B always has more stores than Company A.

Now we will turn our attention to the function representing the number of stores for Company B, [latex]B\left(x\right)=100{\left(1+0.5\right)}^{x}[/latex]. In this exponential function, 100 represents the initial number of stores, 0.5 represents the growth rate, and [latex]1+0.5=1.5[/latex] represents the growth factor. Generalizing further, we can write this function as [latex]B\left(x\right)=100{\left(1.5\right)}^{x}[/latex] where 100 is the initial value, 1.5 is called the base, and x is called the exponent.

Using the Compound Interest Formula

Savings instruments in which earnings are continually reinvested, such as mutual funds and retirement accounts, use compound interest. The term compounding refers to interest earned not only on the original value, but on the accumulated value of the account.

The annual percentage rate (APR) of an account, also called the nominal rate, is the yearly interest rate earned by an investment account. The term nominal is used when the compounding occurs a number of times other than once per year. In fact, when interest is compounded more than once a year, the effective interest rate ends up being greater than the nominal rate! This is a powerful tool for investing.

We can calculate compound interest using the compound interest formula which is an exponential function of the variables time t, principal P, APR r, and number of times compounded in a year n:

[latex]A\left(t\right)=P{\left(1+\frac{r}{n}\right)}^{nt}[/latex]

For example, observe the table below, which shows the result of investing $1,000 at 10% for one year. Notice how the value of the account increases as the compounding frequency increases.

Evaluating Exponential Functions with Base e

As we saw earlier, the amount earned on an account increases as the compounding frequency increases. The table below shows that the increase from annual to semi-annual compounding is larger than the increase from monthly to daily compounding. This might lead us to ask whether this pattern will continue.

Examine the value of $1 invested at 100% interest for 1 year compounded at various frequencies.

These values appear to be approaching a limit as n increases without bound. In fact, as n gets larger and larger, the expression [latex]{\left(1+\frac{1}{n}\right)}^{n}[/latex] approaches a number used so frequently in mathematics that it has its own name: the letter [latex]e[/latex]. This value is an irrational number, which means that its decimal expansion goes on forever without repeating. Its approximation to six decimal places is shown below.

Equations of Exponential Functions

In the previous examples, we were given an exponential function which we then evaluated for a given input. Sometimes we are given information about an exponential function without knowing the function explicitly. We must use the information to first write the form of the function, determine the constants a and b, and evaluate the function.

Example: Writing an Exponential Model When the Initial Value Is Known

In 2006, 80 deer were introduced into a wildlife refuge. By 2012, the population had grown to 180 deer. The population was growing exponentially. Write an algebraic function N(t) representing the population N of deer over time t.

Show Solution

We let our independent variable t be the number of years after 2006. Thus, the information given in the problem can be written as input-output pairs: (0, 80) and (6, 180). Notice that by choosing our input variable to be measured as years after 2006, we have given ourselves the initial value for the function, a = 80. We can now substitute the second point into the equation [latex]N\left(t\right)=80{b}^{t}[/latex] to find b:

[latex]\begin{array}{c}N\left(t\right)\hfill & =80{b}^{t}\hfill & \hfill \\ 180\hfill & =80{b}^{6}\hfill & \text{Substitute using point }\left(6, 180\right).\hfill \\ \frac{9}{4}\hfill & ={b}^{6}\hfill & \text{Divide and write in lowest terms}.\hfill \\ b\hfill & ={\left(\frac{9}{4}\right)}^{\frac{1}{6}}\hfill & \text{Isolate }b\text{ using properties of exponents}.\hfill \\ b\hfill & \approx 1.1447 & \text{Round to 4 decimal places}.\hfill \end{array}[/latex]

NOTE: Unless otherwise stated, do not round any intermediate calculations. Round the final answer to four places for the remainder of this section.

The exponential model for the population of deer is [latex]N\left(t\right)=80{\left(1.1447\right)}^{t}[/latex]. Note that this exponential function models short-term growth. As the inputs get larger, the outputs will get increasingly larger resulting in the model not being useful in the long term due to extremely large output values.

We can graph our model to observe the population growth of deer in the refuge over time. Notice that the graph below passes through the initial points given in the problem, [latex]\left(0,\text{ 8}0\right)[/latex] and [latex]\left(\text{6},\text{ 18}0\right)[/latex]. We can also see that the domain for the function is [latex]\left[0,\infty \right)[/latex] and the range for the function is [latex]\left[80,\infty \right)[/latex].

Graph showing the population of deer over time, [latex]N\left(t\right)=80{\left(1.1447\right)}^{t}[/latex], t years after 2006

Example: Writing an Exponential Model When the Initial Value is Not Known

Find an exponential function that passes through the points [latex]\left(-2,6\right)[/latex] and [latex]\left(2,1\right)[/latex].

Show Solution

Because we don’t have the initial value, we substitute both points into an equation of the form [latex]f\left(x\right)=a{b}^{x}[/latex] and then solve the system for a and b.

• Substituting [latex]\left(-2,6\right)[/latex] gives [latex]6=a{b}^{-2}[/latex]
• Substituting [latex]\left(2,1\right)[/latex] gives [latex]1=a{b}^{2}[/latex]

Use the first equation to solve for a in terms of b:

[latex]\begin{array}{l}6=ab^{-2}\\\frac{6}{b^{-2}}=a\,\,\,\,\,\,\,\,\text{Divide.}\\a=6b^{2}\,\,\,\,\,\,\,\,\text{Use properties of exponents to rewrite the denominator.}\end{array}[/latex]

Substitute a in the second equation and solve for b:

[latex]\begin{array}{l}1=ab^{2}\\1=6b^{2}b^{2}=6b^{4}\,\,\,\,\,\text{Substitute }a.\\b=\left(\frac{1}{6}\right)^{\frac{1}{4}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{Use properties of exponents to isolate }b.\\b\approx0.6389\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{Round 4 decimal places.}\end{array}[/latex]

Use the value of b in the first equation to solve for the value of a:

[latex]a=6b^{2}\approx6\left(0.6389\right)^{2}\approx2.4492[/latex]

Thus, the equation is [latex]f\left(x\right)=2.4492{\left(0.6389\right)}^{x}[/latex].

We can graph our model to check our work. Notice that the graph below passes through the initial points given in the problem, [latex]\left(-2,\text{ 6}\right)[/latex] and [latex]\left(2,\text{ 1}\right)[/latex]. The graph is an example of an exponential decay function.

The graph of [latex]f\left(x\right)=2.4492{\left(0.6389\right)}^{x}[/latex] models exponential decay.

Example: Writing an Exponential Function Given Its Graph

Find an equation for the exponential function graphed below.

Show Solution

We can choose the y-intercept of the graph, [latex]\left(0,3\right)[/latex], as our first point. This gives us the initial value [latex]a=3[/latex]. Next, choose a point on the curve some distance away from [latex]\left(0,3\right)[/latex] that has integer coordinates. One such point is [latex]\left(2,12\right)[/latex].

[latex]\begin{array}{llllll}y=a{b}^{x}& \text{Write the general form of an exponential equation}. \\ y=3{b}^{x} & \text{Substitute the initial value 3 for }a. \\ 12=3{b}^{2} & \text{Substitute in 12 for }y\text{ and 2 for }x. \\ 4={b}^{2} & \text{Divide by 3}. \\ b=\pm 2 & \text{Take the square root}.\end{array}[/latex]

Because we restrict ourselves to positive values of b, we will use b = 2. Substitute a and b into standard form to yield the equation [latex]f\left(x\right)=3{\left(2\right)}^{x}[/latex].

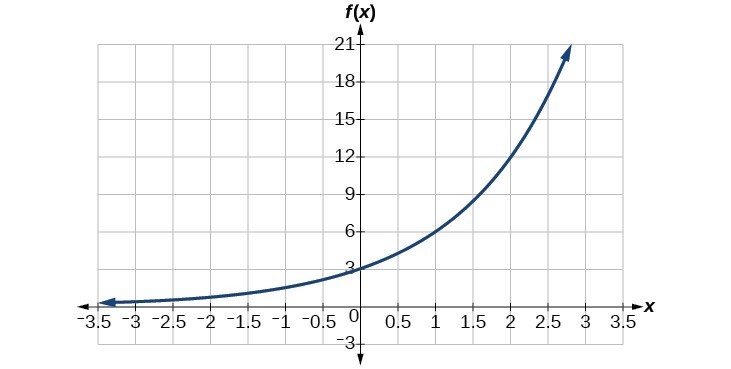
Try It

Find an equation for the exponential function graphed below.

Show Solution

[latex]f\left(x\right)=\sqrt{2}{\left(\sqrt{2}\right)}^{x}[/latex]. Answers may vary due to round-off error. The answer should be very close to [latex]1.4142{\left(1.4142\right)}^{x}[/latex].

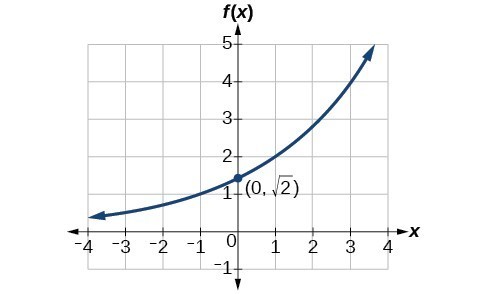
Investigating Continuous Growth

So far we have worked with rational bases for exponential functions. For most real-world phenomena, however, e is used as the base for exponential functions. Exponential models that use e as the base are called continuous growth or decay models. We see these models in finance, computer science, and most of the sciences such as physics, toxicology, and fluid dynamics.