Learning Outcomes
- Use interval notation to express inequalities.
- Use properties of inequalities.
- Solve compound inequalities.
- Solve absolute value inequalities.
It is not easy to make the honor roll at most top universities. Suppose students were required to carry a course load of at least 12 credit hours and maintain a grade point average of 3.5 or above. How could these honor roll requirements be expressed mathematically? In this section, we will explore various ways to express different sets of numbers, inequalities, and absolute value inequalities.

Writing and Manipulating Inequalities
Indicating the solution to an inequality such as [latex]x\ge 4[/latex] can be achieved in several ways.
We can use a number line as shown below. The blue ray begins at [latex]x=4[/latex] and, as indicated by the arrowhead, continues to infinity, which illustrates that the solution set includes all real numbers greater than or equal to 4.
We can use set-builder notation: [latex]\{x|x\ge 4\}[/latex], which translates to “all real numbers x such that x is greater than or equal to 4.” Notice that braces are used to indicate a set.
The third method is interval notation, where solution sets are indicated with parentheses or brackets. The solutions to [latex]x\ge 4[/latex] are represented as [latex]\left[4,\infty \right)[/latex]. This is perhaps the most useful method as it applies to concepts studied later in this course and to other higher-level math courses.
The main concept to remember is that parentheses represent solutions greater or less than the number, and brackets represent solutions that are greater than or equal to or less than or equal to the number. Use parentheses to represent infinity or negative infinity, since positive and negative infinity are not numbers in the usual sense of the word and, therefore, cannot be “equaled.” A few examples of an interval, or a set of numbers in which a solution falls, are [latex]\left[-2,6\right)[/latex], or all numbers between [latex]-2[/latex] and [latex]6[/latex], including [latex]-2[/latex], but not including [latex]6[/latex]; [latex]\left(-1,0\right)[/latex], all real numbers between, but not including [latex]-1[/latex] and [latex]0[/latex]; and [latex]\left(-\infty ,1\right][/latex], all real numbers less than and including [latex]1[/latex]. The table below outlines the possibilities.
| Set Indicated | Set-Builder Notation | Interval Notation |
|---|---|---|
| All real numbers between a and b, but not including a or b | [latex]\{x|a<x<b\}[/latex] | [latex]\left(a,b\right)[/latex] |
| All real numbers greater than a, but not including a | [latex]\{x|x>a\}[/latex] | [latex]\left(a,\infty \right)[/latex] |
| All real numbers less than b, but not including b | [latex]\{x|x<b\}[/latex] | [latex]\left(-\infty ,b\right)[/latex] |
| All real numbers greater than a, including a | [latex]\{x|x\ge a\}[/latex] | [latex]\left[a,\infty \right)[/latex] |
| All real numbers less than b, including b | [latex]\{x|x\le b\}[/latex] | [latex]\left(-\infty ,b\right][/latex] |
| All real numbers between a and b, including a | [latex]\{x|a\le x<b\}[/latex] | [latex]\left[a,b\right)[/latex] |
| All real numbers between a and b, including b | [latex]\{x|a<x\le b\}[/latex] | [latex]\left(a,b\right][/latex] |
| All real numbers between a and b, including a and b | [latex]\{x|a\le x\le b\}[/latex] | [latex]\left[a,b\right][/latex] |
| All real numbers less than a or greater than b | [latex]\{x|x<a\text{ and }x>b\}[/latex] | [latex]\left(-\infty ,a\right)\cup \left(b,\infty \right)[/latex] |
| All real numbers | [latex]\{x|x\text{ is all real numbers}\}[/latex] | [latex]\left(-\infty ,\infty \right)[/latex] |
Example: Using Interval Notation to Express All Real Numbers Greater Than or Equal to a Number
Use interval notation to indicate all real numbers greater than or equal to [latex]-2[/latex].
Try It
Use interval notation to indicate all real numbers between and including [latex]-3[/latex] and [latex]5[/latex].
Example: Using Interval Notation to Express All Real Numbers Less Than or Equal to a or Greater Than or Equal to b
Write the interval expressing all real numbers less than or equal to [latex]-1[/latex] or greater than or equal to [latex]1[/latex].
Try It
Express all real numbers less than [latex]-2[/latex] or greater than or equal to 3 in interval notation.
Using the Properties of Inequalities
When we work with inequalities, we can usually treat them similarly to but not exactly as we treat equations. We can use the addition property and the multiplication property to help us solve them. The one exception is when we multiply or divide by a negative number, we must reverse the inequality symbol.
A General Note: Properties of Inequalities
[latex]\begin{array}{ll}\text{Addition Property}\hfill& \text{If }a< b,\text{ then }a+c< b+c.\hfill \\ \hfill & \hfill \\ \text{Multiplication Property}\hfill & \text{If }a< b\text{ and }c> 0,\text{ then }ac< bc.\hfill \\ \hfill & \text{If }a< b\text{ and }c< 0,\text{ then }ac> bc.\hfill \end{array}[/latex]
These properties also apply to [latex]a\le b[/latex], [latex]a>b[/latex], and [latex]a\ge b[/latex].
Example: Demonstrating the Addition Property
Illustrate the addition property for inequalities by solving each of the following:
- [latex]x - 15<4[/latex]
- [latex]6\ge x - 1[/latex]
- [latex]x+7>9[/latex]
Try It
Solve [latex]3x - 2<1[/latex].
Example: Demonstrating the Multiplication Property
Illustrate the multiplication property for inequalities by solving each of the following:
- [latex]3x<6[/latex]
- [latex]-2x - 1\ge 5[/latex]
- [latex]5-x>10[/latex]
Try It
Solve [latex]4x+7\ge 2x - 3[/latex].
Solving Inequalities in One Variable Algebraically
As the examples have shown, we can perform the same operations on both sides of an inequality, just as we do with equations; we combine like terms and perform operations. To solve, we isolate the variable.
Example: Solving an Inequality Algebraically
Solve the inequality: [latex]13 - 7x\ge 10x - 4[/latex].
Try It
Solve the inequality and write the answer using interval notation: [latex]-x+4<\frac{1}{2}x+1[/latex].
Example: Solving an Inequality with Fractions
Solve the following inequality and write the answer in interval notation: [latex]-\frac{3}{4}x\ge -\frac{5}{8}+\frac{2}{3}x[/latex].
Try It
Solve the inequality and write the answer in interval notation: [latex]-\frac{5}{6}x\le \frac{3}{4}+\frac{8}{3}x[/latex].
Compound and Absolute Value Inequalities
A compound inequality includes two inequalities in one statement. A statement such as [latex]4<x\le 6[/latex] means [latex]4<x[/latex] and [latex]x\le 6[/latex]. There are two ways to solve compound inequalities: separating them into two separate inequalities or leaving the compound inequality intact and performing operations on all three parts at the same time. We will illustrate both methods.
Example: Solving a Compound Inequality
Solve the compound inequality: [latex]3\le 2x+2<6[/latex].
Try It
Solve the compound inequality [latex]4<2x - 8\le 10[/latex].
Example: Solving a Compound Inequality with the Variable in All Three Parts
Solve the compound inequality with variables in all three parts: [latex]3+x>7x - 2>5x - 10[/latex].
Try It
Solve the compound inequality: [latex]3y<4 - 5y<5+3y[/latex].
Solving Absolute Value Inequalities
As we know, the absolute value of a quantity is a positive number or zero. From the origin, a point located at [latex]\left(-x,0\right)[/latex] has an absolute value of [latex]x[/latex] as it is x units away. Consider absolute value as the distance from one point to another point. Regardless of direction, positive or negative, the distance between the two points is represented as a positive number or zero.
An absolute value inequality is an equation of the form
where A, and sometimes B, represents an algebraic expression dependent on a variable x. Solving the inequality means finding the set of all [latex]x[/latex] –values that satisfy the problem. Usually this set will be an interval or the union of two intervals and will include a range of values.
There are two basic approaches to solving absolute value inequalities: graphical and algebraic. The advantage of the graphical approach is we can read the solution by interpreting the graphs of two equations. The advantage of the algebraic approach is that solutions are exact, as precise solutions are sometimes difficult to read from a graph.
Suppose we want to know all possible returns on an investment if we could earn some amount of money within $200 of $600. We can solve algebraically for the set of x-values such that the distance between [latex]x[/latex] and 600 is less than 200. We represent the distance between [latex]x[/latex] and 600 as [latex]|x - 600|[/latex], and therefore, [latex]|x - 600|\le 200[/latex] or
This means our returns would be between $400 and $800.
To solve absolute value inequalities, just as with absolute value equations, we write two inequalities and then solve them independently.
A General Note: Absolute Value Inequalities
For an algebraic expression X and [latex]k>0[/latex], an absolute value inequality is an inequality of the form:
These statements also apply to [latex]|X|\le k[/latex] and [latex]|X|\ge k[/latex].
Example: Determining a Number within a Prescribed Distance
Describe all values [latex]x[/latex] within a distance of 4 from the number 5.
Try It
Describe all x-values within a distance of 3 from the number 2.
Example: Solving an Absolute Value Inequality
Solve [latex]|x - 1|\le 3[/latex].
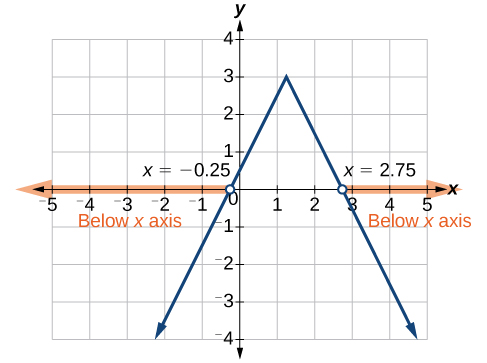
Example: Using a Graphical Approach to Solve Absolute Value Inequalities
Given the equation [latex]y=-\frac{1}{2}|4x - 5|+3[/latex], determine the x-values for which the y-values are negative.
Try It
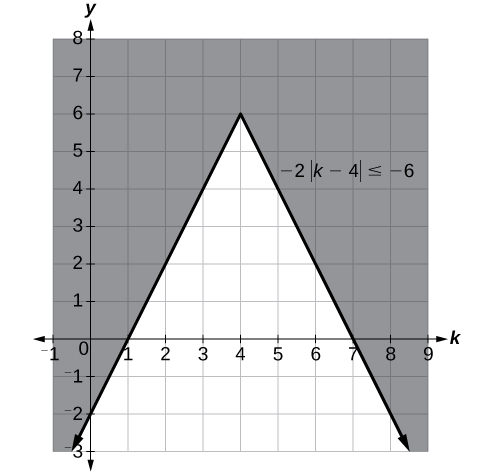
Solve [latex]-2|k - 4|\le -6[/latex].
Key Concepts
- Interval notation is a method to give the solution set of an inequality. Highly applicable in calculus, it is a system of parentheses and brackets that indicate what numbers are included in a set and whether the endpoints are included as well.
- Solving inequalities is similar to solving equations. The same algebraic rules apply, except for one: multiplying or dividing by a negative number reverses the inequality.
- Compound inequalities often have three parts and can be rewritten as two independent inequalities. Solutions are given by boundary values which are indicated as a beginning boundary or an ending boundary in the solutions to the two inequalities.
- Absolute value inequalities will produce two solution sets due to the nature of absolute value. We solve by writing two equations: one equal to a positive value and one equal to a negative value.
- Absolute value inequality solutions can be verified by graphing. We can check the algebraic solutions by graphing as we cannot depend on a visual for a precise solution.
Glossary
- compound inequality
- a problem or a statement that includes two inequalities
- interval
- an interval describes a set of numbers where a solution falls
- interval notation
- a mathematical statement that describes a solution set and uses parentheses or brackets to indicate where an interval begins and ends
- linear inequality
- similar to a linear equation except that the solutions will include an interval of numbers