Learning Outcomes
- Use prescribed strategies to build linear models.
- Use intercepts and data points to build a linear model.
- Use a diagram to build a model.
- Draw and interpret scatter plots.
- Find the line of best fit using a calculator.
- Distinguish between linear and nonlinear relations.
- Use a linear model to make predictions.
Emily is a college student who plans to spend a summer in Seattle. She has saved $3,500 for her trip and anticipates spending $400 each week on rent, food, and activities. How can we write a linear model to represent her situation? What would be the x-intercept, and what can she learn from it? To answer these and related questions, we can create a model using a linear function. Models such as this one can be extremely useful for analyzing relationships and making predictions based on those relationships. In this section, we will explore examples of linear function models.

A view of the Seattle skyline. (credit: EEK Photography/Flickr)
Build Linear Models
When modeling scenarios with linear functions and solving problems involving quantities with a constant rate of change, we typically follow the same problem solving strategies that we would use for any type of function. Let’s briefly review them:
- Identify changing quantities, and then define descriptive variables to represent those quantities. When appropriate, sketch a picture or define a coordinate system.
- Look for information that provides values for the variables or values for parts of the functional model, such as slope and initial value.
- Determine what we are trying to find, identify, solve, or interpret.
- Identify a solution pathway from the provided information to what we are trying to find. Often this will involve checking and tracking units, building a table, or even finding a formula for the function being used to model the problem.
- When needed, write a formula for the function.
- Solve or evaluate the function using the formula.
- Reflect on whether your answer is reasonable for the given situation and whether it makes sense mathematically.
- Clearly convey your result using appropriate units, and answer in full sentences when necessary.
Building Linear Models
Now let’s take a look at the student in Seattle. In her situation, there are two changing quantities: time and money. The amount of money she has remaining while on vacation depends on how long she stays. We can use this information to define our variables, including units.
- Output: M, money remaining, in dollars
- Input: t, time, in weeks
So, the amount of money remaining depends on the number of weeks. Hence, amount of money remaining is a function of time: M(t)
We can also identify the initial value and the rate of change.
- Initial Value: She saved $3,500, so $3,500 is the initial value for M.
- Rate of Change: She anticipates spending $400 each week, so –$400 per week is the rate of change, or slope.
Notice that the unit of dollars per week matches the unit of our output variable divided by our input variable. Also, because the slope is negative, the linear function is decreasing. This should make sense because she is spending money each week.
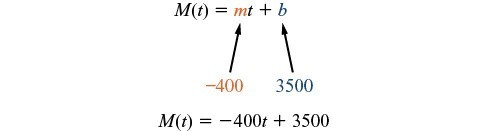
The rate of change is constant, so we can start with the linear model [latex]M(t)=mt+b[/latex]. Then we can substitute the intercept and slope provided.
To find the x-intercept, we set the output to zero and solve for the input.
[latex]\begin{array}{l}0=-400t+3500\hfill \\ t=\frac{3500}{400}\hfill \\ t=8.75\hfill \end{array}[/latex]
The x-intercept is 8.75 weeks. Because this represents the input value when the output will be zero, we could say that Emily will have no money left after 8.75 weeks.
When modeling any real-life scenario with functions, there is typically a limited domain over which that model will be valid—almost no trend continues indefinitely. Here the domain refers to the number of weeks. In this case, it doesn’t make sense to talk about input values less than zero. A negative input value could refer to a number of weeks before she saved $3,500, but the scenario discussed poses the question once she saved $3,500 because this is when her trip and subsequent spending starts. It is also likely that this model is not valid after the x-intercept, unless Emily will use a credit card and goes into debt. The domain represents the set of input values, so the reasonable domain for this function is [latex]0\le t\le 8.75[/latex].
In the above example, we were given a written description of the situation. We followed the steps of modeling a problem to analyze the information. However, the information provided may not always be the same. Sometimes we might be provided with an intercept. Other times we might be provided with an output value. We must be careful to analyze the information we are given and use it appropriately to build a linear model.
Using a Given Intercept to Build a Model
Some real-world problems provide the y-intercept, which is the constant or initial value. Once the y-intercept is known, the x-intercept can be calculated. Suppose, for example, that Hannah plans to pay off a no-interest loan from her parents. Her loan balance is $1,000. She plans to pay $250 per month until her balance is $0. The y-intercept is the initial amount of her debt, or $1,000. The rate of change, or slope, is –$250 per month. We can then use slope-intercept form and the given information to develop a linear model.
[latex]\begin{array}{l}f\left(x\right)=mx+b\hfill \\ f\left(x\right)=-250x+1000\hfill \end{array}[/latex]
Now we can set the function equal to 0 and solve for x to find the x-intercept.
[latex]\begin{array}{l}0=-250x+1000\hfill \\ 1000=250x\hfill \\ 4=x\hfill \\ x=4\hfill \end{array}[/latex]
The x-intercept is the number of months it takes her to reach a balance of $0. The x-intercept is 4 months, so it will take Hannah four months to pay off her loan.
Using a Given Input and Output to Build a Model
Many real-world applications are not as direct as the ones we just considered. Instead they require us to identify some aspect of a linear function. We might sometimes be asked to evaluate the linear model at a given input or set the equation of the linear model equal to a specified output.
How To: Given a word problem that includes two pairs of input and output values, use the linear function to solve a problem.
- Identify the input and output values.
- Convert the data to two coordinate pairs.
- Find the slope.
- Write the linear model.
- Use the model to make a prediction by evaluating the function at a given x value.
- Use the model to identify an x value that results in a given y value.
- Answer the question posed.
Example: Using a Linear Model to Investigate a Town’s Population
A town’s population has been growing linearly. In 2004 the population was 6,200. By 2009 the population had grown to 8,100. Assume this trend continues.
- Predict the population in 2013.
- Identify the year in which the population will reach 15,000.
Try It
A company sells doughnuts. They incur a fixed cost of $25,000 for rent, insurance, and other expenses. It costs $0.25 to produce each doughnut.
- Write a linear model to represent the cost C of the company as a function of x, the number of doughnuts produced.
- Find and interpret the y-intercept.
Try It
A city’s population has been growing linearly. In 2008, the population was 28,200. By 2012, the population was 36,800. Assume this trend continues.
- Predict the population in 2014.
- Identify the year in which the population will reach 54,000.
Using a Diagram to Model a Problem
It is useful for many real-world applications to draw a picture to gain a sense of how the variables representing the input and output may be used to answer a question. To draw the picture, first consider what the problem is asking for. Then, determine the input and the output. The diagram should relate the variables. Often, geometric shapes or figures are drawn. Distances are often traced out. If a right triangle is sketched, the Pythagorean Theorem relates the sides. If a rectangle is sketched, labeling width and height is helpful.
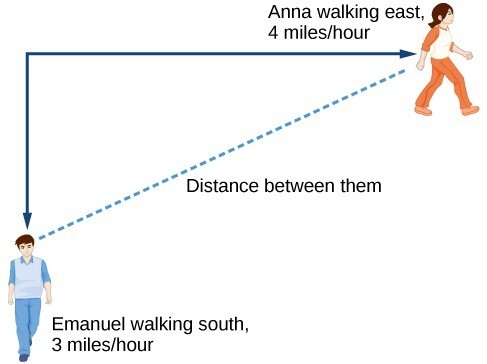
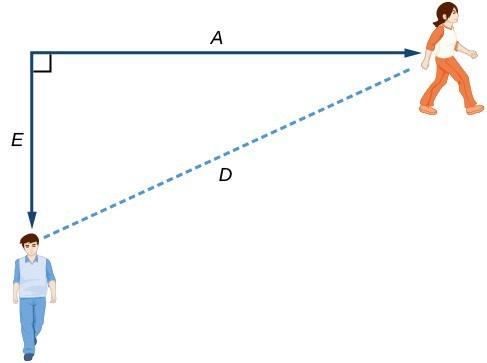
Example: Using a Diagram to Model Distance Walked
Anna and Emanuel start at the same intersection. Anna walks east at 4 miles per hour while Emanuel walks south at 3 miles per hour. They are communicating with a two-way radio that has a range of 2 miles. How long after they start walking will they fall out of radio contact?
Q & A
Should I draw diagrams when given information based on a geometric shape?
Yes. Sketch the figure and label the quantities and unknowns on the sketch.
Example: Using a Diagram to Model Distance between Cities
There is a straight road leading from the town of Westborough to Agritown 30 miles east and 10 miles north. A certain distance down this road, it junctions with a second road, perpendicular to the first, leading to the town of Eastborough. If the town of Eastborough is located 20 miles directly east of the town of Westborough, how far is the road junction from Westborough?
Try It
There is a straight road leading from the town of Timpson to Ashburn 60 miles east and 12 miles north. Partway down the road, it junctions with a second road, perpendicular to the first, leading to the town of Garrison. If the town of Garrison is located 22 miles directly east of the town of Timpson, how far is the road junction from Timpson?
Fitting Linear Models to Data
A professor is attempting to identify trends among final exam scores. His class has a mixture of students, so he wonders if there is any relationship between age and final exam scores. One way for him to analyze the scores is by creating a diagram that relates the age of each student to the exam score received. In this section, we will examine one such diagram known as a scatter plot.
A scatter plot is a graph of plotted points that may show a relationship between two sets of data. If the relationship is from a linear model, or a model that is nearly linear, the professor can draw conclusions using his knowledge of linear functions. Below is a sample scatter plot.
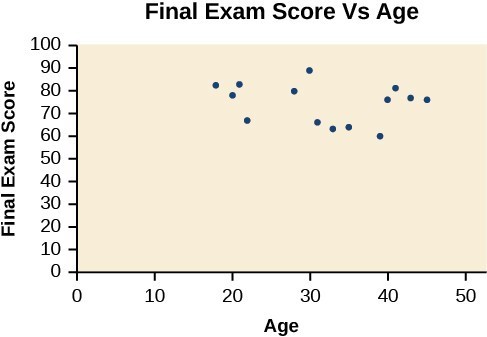
A scatter plot of age and final exam score variables.
Notice this scatter plot does not indicate a linear relationship. The points do not appear to follow a trend. In other words, there does not appear to be a relationship between the age of the student and the score on the final exam.
Example: Using a Scatter Plot to Investigate Cricket Chirps
The table below shows the number of cricket chirps in 15 seconds, for several different air temperatures, in degrees Fahrenheit.[1] Plot this data and determine whether the data appears to be linearly related.
| Chirps | 44 | 35 | 20.4 | 33 | 31 | 35 | 18.5 | 37 | 26 |
| Temperature | 80.5 | 70.5 | 57 | 66 | 68 | 72 | 52 | 73.5 | 53 |
Finding the Line of Best Fit
One way to approximate our linear function is to sketch the line that seems to best fit the data. Then we can extend the line until we can verify the y-intercept. We can approximate the slope of the line by extending it until we can estimate the [latex]\frac{\text{rise}}{\text{run}}[/latex].
Example: Finding a Line of Best Fit
Find a linear function that fits the data in the table below by “eyeballing” a line that seems to fit.
| Chirps | 44 | 35 | 20.4 | 33 | 31 | 35 | 18.5 | 37 | 26 |
| Temperature | 80.5 | 70.5 | 57 | 66 | 68 | 72 | 52 | 73.5 | 53 |
Try It
Recognizing Interpolation or Extrapolation
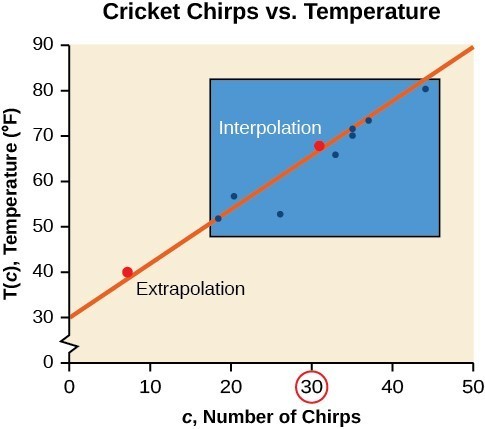
While the data for most examples does not fall perfectly on the line, the equation is our best guess as to how the relationship will behave outside of the values for which we have data. We use a process known as interpolation when we predict a value inside the domain and range of the data. The process of extrapolation is used when we predict a value outside the domain and range of the data.
The graph below compares the two processes for the cricket-chirp data addressed in the previous example. We can see that interpolation would occur if we used our model to predict temperature when the values for chirps are between 18.5 and 44. Extrapolation would occur if we used our model to predict temperature when the values for chirps are less than 18.5 or greater than 44.
There is a difference between making predictions inside the domain and range of values for which we have data and outside that domain and range. Predicting a value outside of the domain and range has its limitations. When our model no longer applies after a certain point, it is sometimes called model breakdown. For example, predicting a cost function for a period of two years may involve examining the data where the input is the time in years and the output is the cost. But if we try to extrapolate a cost when [latex]x=50[/latex], that is, in 50 years, the model would not apply because we could not account for factors fifty years in the future.
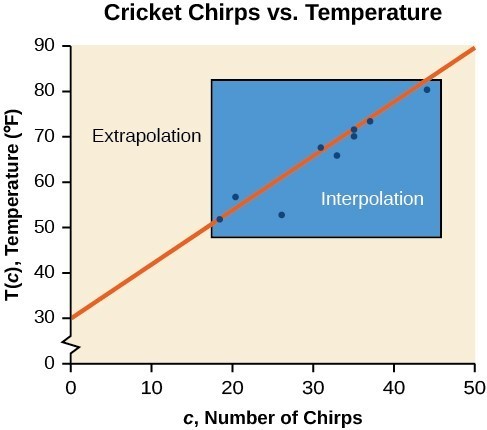
Interpolation occurs within the domain and range of the provided data whereas extrapolation occurs outside.
A General Note: Interpolation and Extrapolation
Different methods of making predictions are used to analyze data.
- The method of interpolation involves predicting a value inside the domain and/or range of the data.
- The method of extrapolation involves predicting a value outside the domain and/or range of the data.
- Model breakdown occurs at the point when the model no longer applies.
Example: Understanding Interpolation and Extrapolation
| Chirps | 44 | 35 | 20.4 | 33 | 31 | 35 | 18.5 | 37 | 26 |
| Temperature | 80.5 | 70.5 | 57 | 66 | 68 | 72 | 52 | 73.5 | 53 |
Use the cricket data above to answer the following questions:
- Would predicting the temperature when crickets are chirping 30 times in 15 seconds be interpolation or extrapolation? Make the prediction, and discuss whether it is reasonable.
- Would predicting the number of chirps crickets will make at 40 degrees be interpolation or extrapolation? Make the prediction, and discuss whether it is reasonable.
Try It
According to the data from the table in the cricket-chirp example, what temperature can we predict if we counted 20 chirps in 15 seconds?
Finding the Line of Best Fit Using a Graphing Utility
While eyeballing a line works reasonably well, there are statistical techniques for fitting a line to data that minimize the differences between the line and data values.[2] One such technique is called least squares regression and can be computed by many graphing calculators as well as spreadsheet and statistical software. Least squares regression is also called linear regression.
Example: Finding a Least Squares Regression Line
Find the least squares regression line using the cricket-chirp data in the table below.
| Chirps | 44 | 35 | 20.4 | 33 | 31 | 35 | 18.5 | 37 | 26 |
| Temperature | 80.5 | 70.5 | 57 | 66 | 68 | 72 | 52 | 73.5 | 53 |
Q & A
Will there ever be a case where two different lines will serve as the best fit for the data?
No. There is only one best fit line.
Distinguish Between Linear and Nonlinear Relations
As we saw in the cricket-chirp example, some data exhibit strong linear trends, but other data, like the final exam scores plotted by age, are clearly nonlinear. Most calculators and computer software can also provide us with the correlation coefficient, which is a measure of how closely the line fits the data. Many graphing calculators require the user to turn a “diagnostic on” selection to find the correlation coefficient, which mathematicians label as r. The correlation coefficient provides an easy way to get an idea of how close to a line the data falls.
We should compute the correlation coefficient only for data that follows a linear pattern or to determine the degree to which a data set is linear. If the data exhibits a nonlinear pattern, the correlation coefficient for a linear regression is meaningless. To get a sense of the relationship between the value of r and the graph of the data, the image below shows some large data sets with their correlation coefficients. Remember, for all plots, the horizontal axis shows the input and the vertical axis shows the output.
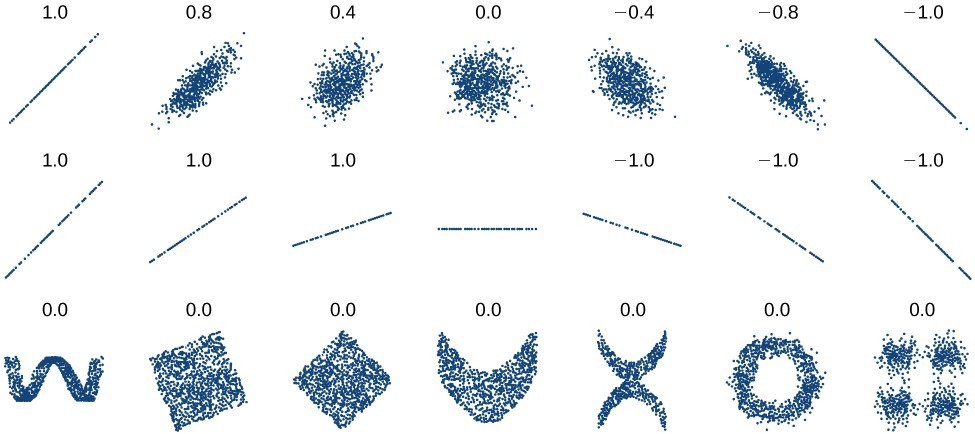
Plotted data and related correlation coefficients. (credit: “DenisBoigelot,” Wikimedia Commons)
A General Note: Correlation Coefficient
The correlation coefficient is a value, r, between –1 and 1.
- r > 0 suggests a positive (increasing) relationship
- r < 0 suggests a negative (decreasing) relationship
- The closer the value is to 0, the more scattered the data.
- The closer the value is to 1 or –1, the less scattered the data is.
Example: Finding a Correlation Coefficient
Calculate the correlation coefficient for cricket-chirp data in the table below.
| Chirps | 44 | 35 | 20.4 | 33 | 31 | 35 | 18.5 | 37 | 26 |
| Temperature | 80.5 | 70.5 | 57 | 66 | 68 | 72 | 52 | 73.5 | 53 |
Use a Linear Model to Make Predictions
Once we determine that a set of data is linear using the correlation coefficient, we can use the regression line to make predictions. As we learned previously, a regression line is a line that is closest to the data in the scatter plot, which means that only one such line is a best fit for the data.
Example: Using a Regression Line to Make Predictions
Gasoline consumption in the United States has been steadily increasing. Consumption data from 1994 to 2004 is shown in the table below.[3] Determine whether the trend is linear, and if so, find a model for the data. Use the model to predict the consumption in 2008.Is this an interpolation or an extrapolation?
| Year | ’94 | ’95 | ’96 | ’97 | ’98 | ’99 | ’00 | ’01 | ’02 | ’03 | ’04 |
| Consumption (billions of gallons) | 113 | 116 | 118 | 119 | 123 | 125 | 126 | 128 | 131 | 133 | 136 |
Try It
Use your calculator or statistical software to find a linear regression for the following data, which represents the amount of time a scuba diver can spend underwater as a function of the depth of the water.
| Depth (feet) | Time (minutes) |
| 50 | 80 |
| 60 | 55 |
| 70 | 45 |
| 80 | 35 |
| 90 | 25 |
| 100 | 22 |
1) Write the equation for the least squares regression line.
2) According to the regression line, how long can a diver spend at a depth of 110 feet?
3)How about 120 feet? Why doesn’t this make sense?
4) At what depth would the dive time be zero?
try it
Here are more data sets that you can plot in your calculator or statistical software. Fit a linear regression for them then interpre the correlation coefficient to determine whether there appears to be a linear relationship.
| Depth of the Columbia River | Water Velocity |
| 0.66 | 1.55 |
| 1.98 | 1.11 |
| 2.64 | 1.42 |
| 3.3 | 1.39 |
| 4.62 | 1.39 |
| 5.94 | 1.14 |
| 7.26 | 0.91 |
| 8.58 | 0.59 |
| 9.9 | 0.59 |
| 10.56 | 0.41 |
| 11.22 | 0.22 |
| % of Mississippi River in Crops (By Basin) | Nitrate Concentration (mg/ L) |
| 2.4 | 0.647 |
| 1.3 | 1.062 |
| 14.3 | 1.432 |
| 0.5 | 0.579 |
| 45.6 | 3.561 |
| 46.6 | 3.938 |
| 1.5 | 0.927 |
| 53.6 | 2.549 |
| 4.1 | 0.357 |
| 3.1 | 0.245 |
Dimensions of the Lava Dome in Mt. St. Helens, t = 0 on 18 October 1980 (eruption was 18 May 1980).
| Days | Millions of Cubic Meters |
| 0 | 2.9 |
| 70 | 13 |
| 109 | 28 |
| 173 | 40 |
| 242 | 56 |
| 322 | 64 |
| 376 | 75 |
| 547 | 88 |
| 603 | 100 |
| 699 | 115 |
| 872 | 152 |
| 922 | 154 |
| 1087 | 173 |
| 1343 | 178 |
| 1692 | 212 |
| 1858 | 243 |
FYI
Divers who want or need to descend to depths greater than 100 feet employ different techniques and equipment to help them safely navigate the depth. For example, different gas mixtures or rebreather equipment may be used. Gas mixtures such as oxygen, helium, and nitrogen can help to mitigate the narcotic effects of breathing gas at great depths.[4]

A scuba diver using rebreather with open circuit bailout cylinders returning from a 600-foot (180 m) dive.
Key Concepts
- Scatter plots show the relationship between two sets of data.
- Scatter plots may represent linear or non-linear models.
- The line of best fit may be estimated or calculated using a calculator or statistical software.
- Interpolation can be used to predict values inside the domain and range of the data, whereas extrapolation can be used to predict values outside the domain and range of the data.
- The correlation coefficient, r, indicates the degree of linear relationship between data.
- A regression line best fits the data.
- The least squares regression line is found by minimizing the squares of the distances of points from a line passing through the data and may be used to make predictions regarding either of the variables.
Glossary
- correlation coefficient
- a value, r, between –1 and 1 that indicates the degree of linear correlation of variables or how closely a regression line fits a data set.
- extrapolation
- predicting a value outside the domain and range of the data
- interpolation
- predicting a value inside the domain and range of the data
- least squares regression
- a statistical technique for fitting a line to data in a way that minimizes the differences between the line and data values
- model breakdown
- when a model no longer applies after a certain point
- Selected data from http://classic.globe.gov/fsl/scientistsblog/2007/10/. Retrieved Aug 3, 2010 ↵
- Technically, the method minimizes the sum of the squared differences in the vertical direction between the line and the data values. ↵
- http://www.bts.gov/publications/national_transportation_statistics/2005/html/table_04_10.html ↵
- https://en.wikipedia.org/wiki/Trimix_(breathing_gas) ↵