Learning Outcomes
- Write a linear equation to express the relationship between unknown quantities.
- Write a linear equation that models two different cell phone packages.
- Use a linear model to answer questions.
- Set up a linear equation involving distance, rate, and time.
- Find the dimensions of a rectangle given the area.
- Find the dimensions of a box given information about its side lengths.
Josh is hoping to get an A in his college algebra class. He has scores of 75, 82, 95, 91, and 94 on his first five tests. Only the final exam remains, and the maximum of points that can be earned is 100. Is it possible for Josh to end the course with an A? A simple linear equation will give Josh his answer.

College students taking an exam. Credit: Kevin Dooley
Many real-world applications can be modeled by linear equations. For example, a cell phone package may include a monthly service fee plus a charge per minute of talk-time; it costs a widget manufacturer a certain amount to produce x widgets per month plus monthly operating charges; a car rental company charges a daily fee plus an amount per mile driven. These are examples of applications we come across every day that are modeled by linear equations. In this section, we will set up and use linear equations to solve such problems.
Writing a Linear Equation to Solve an Application
To set up or model a linear equation to fit a real-world application, we must first determine the known quantities and define the unknown quantity as a variable. Then, we begin to interpret the words as mathematical expressions using mathematical symbols. Let us use the car rental example above. In this case, a known cost, such as $0.10/mi, is multiplied by an unknown quantity, the number of miles driven. Therefore, we can write [latex]0.10x[/latex]. This expression represents a variable cost because it changes according to the number of miles driven.
If a quantity is independent of a variable, we usually just add or subtract it according to the problem. As these amounts do not change, we call them fixed costs. Consider a car rental agency that charges $0.10/mi plus a daily fee of $50. We can use these quantities to model an equation that can be used to find the daily car rental cost [latex]C[/latex].
When dealing with real-world applications, there are certain expressions that we can translate directly into math. The table lists some common verbal expressions and their equivalent mathematical expressions.
| Verbal | Translation to Math Operations |
|---|---|
| One number exceeds another by a | [latex]x,\text{ }x+a[/latex] |
| Twice a number | [latex]2x[/latex] |
| One number is a more than another number | [latex]x,\text{ }x+a[/latex] |
| One number is a less than twice another number | [latex]x,2x-a[/latex] |
| The product of a number and a, decreased by b | [latex]ax-b[/latex] |
| The quotient of a number and the number plus a is three times the number | [latex]\frac{x}{x+a}=3x[/latex] |
| The product of three times a number and the number decreased by b is c | [latex]3x\left(x-b\right)=c[/latex] |
How To: Given a real-world problem, model a linear equation to fit it
- Identify known quantities.
- Assign a variable to represent the unknown quantity.
- If there is more than one unknown quantity, find a way to write the second unknown in terms of the first.
- Write an equation interpreting the words as mathematical operations.
- Solve the equation. Be sure the solution can be explained in words including the units of measure.
Example: Modeling a Linear Equation to Solve an Unknown Number Problem
Find a linear equation to solve for the following unknown quantities: One number exceeds another number by [latex]17[/latex] and their sum is [latex]31[/latex]. Find the two numbers.
Try It
Find a linear equation to solve for the following unknown quantities: One number is three more than twice another number. If the sum of the two numbers is [latex]36[/latex], find the numbers.
Example: Setting Up a Linear Equation to Solve a Real-World Application
There are two cell phone companies that offer different packages. Company A charges a monthly service fee of $34 plus $.05/min talk-time. Company B charges a monthly service fee of $40 plus $.04/min talk-time.
- Write a linear equation that models the packages offered by both companies.
- If the average number of minutes used each month is 1,160, which company offers the better plan?
- If the average number of minutes used each month is 420, which company offers the better plan?
- How many minutes of talk-time would yield equal monthly statements from both companies?
Try It
Find a linear equation to model this real-world application: It costs ABC electronics company $2.50 per unit to produce a part used in a popular brand of desktop computers. The company has monthly operating expenses of $350 for utilities and $3,300 for salaries. What are the company’s monthly expenses?
Using Formulas to Solve Problems
Many applications are solved using known formulas. The problem is stated, a formula is identified, the known quantities are substituted into the formula, the equation is solved for the unknown, and the problem’s question is answered. Typically, these problems involve two equations representing two trips, two investments, two areas, and so on. Examples of formulas include the area of a rectangular region, [latex]A=LW[/latex]; the perimeter of a rectangle, [latex]P=2L+2W[/latex]; and the volume of a rectangular solid, [latex]V=LWH[/latex]. When there are two unknowns, we find a way to write one in terms of the other because we can solve for only one variable at a time.
Example: Solving an Application Using a Formula
It takes Andrew 30 minutes to drive to work in the morning. He drives home using the same route, but it takes 10 minutes longer, and he averages 10 mi/h less than in the morning. How far does Andrew drive to work?
Try It
On Saturday morning, it took Jennifer 3.6 hours to drive to her mother’s house for the weekend. On Sunday evening, due to heavy traffic, it took Jennifer 4 hours to return home. Her speed was 5 mi/h slower on Sunday than on Saturday. What was her speed on Sunday?
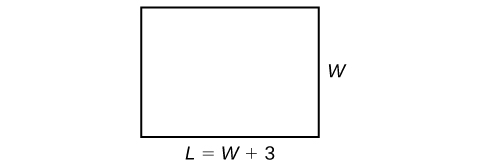
Example: Solving a Perimeter Problem
The perimeter of a rectangular outdoor patio is [latex]54[/latex] ft. The length is [latex]3[/latex] ft. greater than the width. What are the dimensions of the patio?
Try It
Find the dimensions of a rectangle given that the perimeter is [latex]110[/latex] cm. and the length is 1 cm. more than twice the width.
Example: Solving an Area Problem
The perimeter of a tablet of graph paper is 48 in2. The length is [latex]6[/latex] in. more than the width. Find the area of the graph paper.
Try It
A game room has a perimeter of 70 ft. The length is five more than twice the width. How many ft2 of new carpeting should be ordered?
Example: Solving a Volume Problem
Find the dimensions of a shipping box given that the length is twice the width, the height is [latex]8[/latex] inches, and the volume is 1,600 in.3.
Key Concepts
- A linear equation can be used to solve for an unknown in a number problem.
- Applications can be written as mathematical problems by identifying known quantities and assigning a variable to unknown quantities.
- There are many known formulas that can be used to solve applications. Distance problems, for example, are solved using the [latex]d=rt[/latex] formula.
- Many geometry problems are solved using the perimeter formula [latex]P=2L+2W[/latex], the area formula [latex]A=LW[/latex], or the volume formula [latex]V=LWH[/latex].
Glossary
- area
- in square units, the area formula used in this section is used to find the area of any two-dimensional rectangular region: [latex]A=LW[/latex]
- perimeter
- in linear units, the perimeter formula is used to find the linear measurement, or outside length and width, around a two-dimensional regular object; for a rectangle: [latex]P=2L+2W[/latex]
- volume
- in cubic units, the volume measurement includes length, width, and depth: [latex]V=LWH[/latex]
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
- Question ID 52436. Authored by: Edward Wicks. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 7647, 7679. Authored by: Tyler Wallace. License: CC BY: Attribution. License Terms: IMathAS Community License CC- BY + GPL
- Question ID 30987, 13665. Authored by: James Sousa. License: CC BY: Attribution. License Terms: IMathAS Community License CC- BY + GPL
- Question ID 92426. Authored by: Michael Jenck. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 1688. Authored by: WebWork-Rochester. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL