Learning Outcomes
- Solve systems of equations by graphing, substitution, and addition.
- Identify inconsistent systems of equations containing two variables.
- Express the solution of a system of dependent equations containing two variables using standard notations.
A skateboard manufacturer introduces a new line of boards. The manufacturer tracks its costs, which is the amount it spends to produce the boards, and its revenue, which is the amount it earns through sales of its boards. How can the company determine if it is making a profit with its new line? How many skateboards must be produced and sold before a profit is possible? In this section we will consider linear equations with two variables to answer these and similar questions.

(credit: Thomas Sørenes)
Introduction to Solutions of Systems
In order to investigate situations such as that of the skateboard manufacturer, we need to recognize that we are dealing with more than one variable and likely more than one equation. A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously. To find the unique solution to a system of linear equations, we must find a numerical value for each variable in the system that will satisfy all equations in the system at the same time. Some linear systems may not have a solution and others may have an infinite number of solutions. In order for a linear system to have a unique solution, there must be at least as many equations as there are variables. Even so, this does not guarantee a unique solution.
In this section, we will look at systems of linear equations in two variables, which consist of two equations that contain two different variables. For example, consider the following system of linear equations in two variables.
[latex]\begin{align}2x+y&=15\\[1mm] 3x-y&=5\end{align}[/latex]
The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair [latex](4,7)[/latex] is the solution to the system of linear equations. We can verify the solution by substituting the values into each equation to see if the ordered pair satisfies both equations. Shortly we will investigate methods of finding such a solution if it exists.
[latex]\begin{align}2\left(4\right)+\left(7\right)&=15 &&\text{True} \\[1mm] 3\left(4\right)-\left(7\right)&=5 &&\text{True} \end{align}[/latex]
In addition to considering the number of equations and variables, we can categorize systems of linear equations by the number of solutions. A consistent system of equations has at least one solution. A consistent system is considered to be an independent system if it has a single solution, such as the example we just explored. The two lines have different slopes and intersect at one point in the plane. A consistent system is considered to be a dependent system if the equations have the same slope and the same y-intercepts. In other words, the lines coincide so the equations represent the same line. Every point on the line represents a coordinate pair that satisfies the system. Thus, there are an infinite number of solutions.
Another type of system of linear equations is an inconsistent system, which is one in which the equations represent two parallel lines. The lines have the same slope and different y-intercepts. There are no points common to both lines; hence, there is no solution to the system.
A General Note: Types of Linear Systems
There are three types of systems of linear equations in two variables, and three types of solutions.
- An independent system has exactly one solution pair [latex]\left(x,y\right)[/latex]. The point where the two lines intersect is the only solution.
- An inconsistent system has no solution. Notice that the two lines are parallel and will never intersect.
- A dependent system has infinitely many solutions. The lines are coincident. They are the same line, so every coordinate pair on the line is a solution to both equations.
Below is a comparison of graphical representations of each type of system.

How To: Given a system of linear equations and an ordered pair, determine whether the ordered pair is a solution.
- Substitute the ordered pair into each equation in the system.
- Determine whether true statements result from the substitution in both equations; if so, the ordered pair is a solution.
Example: Determining Whether an Ordered Pair Is a Solution to a System of Equations
Determine whether the ordered pair [latex]\left(5,1\right)[/latex] is a solution to the given system of equations.
[latex]\begin{align}x+3y&=8\\ 2x-9&=y \end{align}[/latex]
Try It
Determine whether the ordered pair [latex]\left(8,5\right)[/latex] is a solution to the following system.
[latex]\begin{align}5x-4y&=20\\ 2x+1&=3y\end{align}[/latex]
Solving Systems of Equations by Graphing
There are multiple methods of solving systems of linear equations. For a system of linear equations in two variables, we can determine both the type of system and the solution by graphing the system of equations on the same set of axes.
Example: Solving a System of Equations in Two Variables by Graphing
Solve the following system of equations by graphing. Identify the type of system.
[latex]\begin{align}2x+y&=-8\\ x-y&=-1\end{align}[/latex]
Try It
Solve the following system of equations by graphing.
[latex]\begin{gathered}2x - 5y=-25 \\ -4x+5y=35 \end{gathered}[/latex]
Q& A
Can graphing be used if the system is inconsistent or dependent?
Yes, in both cases we can still graph the system to determine the type of system and solution. If the two lines are parallel, the system has no solution and is inconsistent. If the two lines are identical, the system has infinite solutions and is a dependent system.
Try it
Plot the three different systems with an online graphing tool. Categorize each solution as either consistent or inconsistent. If the system is consistent determine whether it is dependent or independent. You may find it easier to plot each system individually, then clear out your entries before you plot the next.
1)
[latex]5x-3y = -19[/latex]
[latex]x=2y-1[/latex]
2)
[latex]4x+y=11[/latex]
[latex]-2y=-25+8x[/latex]
3)
[latex]y = -3x+6[/latex]
[latex]-\frac{1}{3}y+2=x[/latex]
Solving Systems of Equations by Substitution
Solving a linear system in two variables by graphing works well when the solution consists of integer values, but if our solution contains decimals or fractions, it is not the most precise method. We will consider two more methods of solving a system of linear equations that are more precise than graphing. One such method is solving a system of equations by the substitution method, in which we solve one of the equations for one variable and then substitute the result into the second equation to solve for the second variable. Recall that we can solve for only one variable at a time, which is the reason the substitution method is both valuable and practical.
How To: Given a system of two equations in two variables, solve using the substitution method.
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the second equation, then solve for the remaining variable.
- Substitute that solution into either of the original equations to find the value of the first variable. If possible, write the solution as an ordered pair.
- Check the solution in both equations.
Example: Solving a System of Equations in Two Variables by Substitution
Solve the following system of equations by substitution.
[latex]\begin{align}-x+y&=-5 \\ 2x-5y&=1 \end{align}[/latex]
Try It
Solve the following system of equations by substitution.
[latex]\begin{align}x&=y+3 \\ 4&=3x - 2y \end{align}[/latex]
Q & A
Can the substitution method be used to solve any linear system in two variables?
Yes, but the method works best if one of the equations contains a coefficient of 1 or –1 so that we do not have to deal with fractions.
The following video is ~10 minutes long and provides a mini-lesson on using the substitution method to solve a system of linear equations. We present three different examples, and also use a graphing tool to help summarize the solution for each example.
Solving Systems of Equations in Two Variables by the Addition Method
A third method of solving systems of linear equations is the addition method, this method is also called the elimination method. In this method, we add two terms with the same variable, but opposite coefficients, so that the sum is zero. Of course, not all systems are set up with the two terms of one variable having opposite coefficients. Often we must adjust one or both of the equations by multiplication so that one variable will be eliminated by addition.
How To: Given a system of equations, solve using the addition method.
- Write both equations with x– and y-variables on the left side of the equal sign and constants on the right.
- Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
- Solve the resulting equation for the remaining variable.
- Substitute that value into one of the original equations and solve for the second variable.
- Check the solution by substituting the values into the other equation.
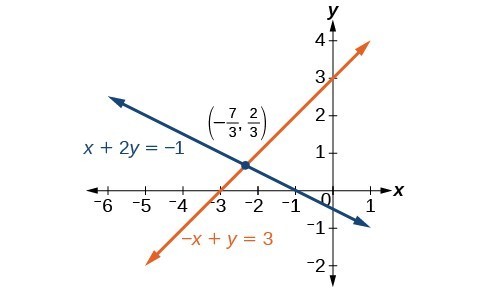
Example: Solving a System by the Addition Method
Solve the given system of equations by addition.
[latex]\begin{align}x+2y&=-1 \\ -x+y&=3 \end{align}[/latex]
Try IT
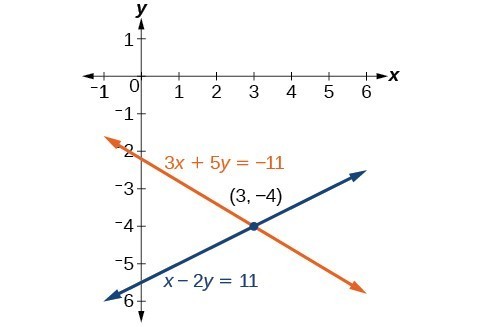
Example: Using the Addition Method When Multiplication of One Equation Is Required
Solve the given system of equations by the addition method.
[latex]\begin{align}3x+5y&=-11 \\ x - 2y&=11 \end{align}[/latex]
Try It
Solve the system of equations by addition.
[latex]\begin{align}2x - 7y&=2\\ 3x+y&=-20\end{align}[/latex]
Example: Using the Addition Method When Multiplication of Both Equations Is Required
Solve the given system of equations in two variables by addition.
[latex]\begin{align}2x+3y&=-16 \\ 5x - 10y&=30\end{align}[/latex]
Example: Using the Addition Method in Systems of Equations Containing Fractions
Solve the given system of equations in two variables by addition.
[latex]\begin{align}\frac{x}{3}+\frac{y}{6}&=3 \\[1mm] \frac{x}{2}-\frac{y}{4}&=1 \end{align}[/latex]
Try It
Solve the system of equations by addition.
[latex]\begin{align}2x+3y&=8\\ 3x+5y&=10\end{align}[/latex]
in the following video we present more examples of how to use the addition (elimination) method to solve a system of two linear equations.
Classify Solutions to Systems
Now that we have several methods for solving systems of equations, we can use the methods to identify inconsistent systems. Recall that an inconsistent system consists of parallel lines that have the same slope but different [latex]y[/latex] -intercepts. They will never intersect. When searching for a solution to an inconsistent system, we will come up with a false statement, such as [latex]12=0[/latex].
Example: Solving an Inconsistent System of Equations
Solve the following system of equations.
[latex]\begin{gathered}&x=9 - 2y \\ &x+2y=13 \end{gathered}[/latex]
Try It
Solve the following system of equations in two variables.
[latex]\begin{gathered}2y - 2x=2\\ 2y - 2x=6\end{gathered}[/latex]
Expressing the Solution of a System of Dependent Equations Containing Two Variables
Recall that a dependent system of equations in two variables is a system in which the two equations represent the same line. Dependent systems have an infinite number of solutions because all of the points on one line are also on the other line. After using substitution or addition, the resulting equation will be an identity, such as [latex]0=0[/latex].
Example: Finding a Solution to a Dependent System of Linear Equations
Find a solution to the system of equations using the addition method.
[latex]\begin{gathered}x+3y=2\\ 3x+9y=6\end{gathered}[/latex]
Writing the general solution
In the previous example, we presented an analysis of the solution to the following system of equations:
[latex]\begin{gathered}x+3y=2\\ 3x+9y=6\end{gathered}[/latex]
After a little algebra, we found that these two equations were exactly the same. We then wrote the general solution as [latex]\left(x, -\frac{1}{3}x+\frac{2}{3}\right)[/latex]. Why would we write the solution this way? In some ways, this representation tells us a lot. It tells us that x can be anything, x is x. It also tells us that y is going to depend on x, just like when we write a function rule. In this case, depending on what you put in for x, y will be defined in terms of x as [latex]-\frac{1}{3}x+\frac{2}{3}[/latex].
In other words, there are infinitely many (x,y) pairs that will satisfy this system of equations, and they all fall on the line [latex]f(x)-\frac{1}{3}x+\frac{2}{3}[/latex].
Try It
Solve the following system of equations in two variables.
[latex]\begin{gathered}y - 2x=5 \\ -3y+6x=-15 \end{gathered}[/latex]
Using Systems of Equations to Investigate Profits
Using what we have learned about systems of equations, we can return to the skateboard manufacturing problem at the beginning of the section. The skateboard manufacturer’s revenue function is the function used to calculate the amount of money that comes into the business. It can be represented by the equation [latex]R=xp[/latex], where [latex]x=[/latex] quantity and [latex]p=[/latex] price. The revenue function is shown in orange in the graph below.
The cost function is the function used to calculate the costs of doing business. It includes fixed costs, such as rent and salaries, and variable costs, such as utilities. The cost function is shown in blue in the graph below. The x-axis represents quantity in hundreds of units. The y-axis represents either cost or revenue in hundreds of dollars.

The point at which the two lines intersect is called the break-even point. We can see from the graph that if 700 units are produced, the cost is $3,300 and the revenue is also $3,300. In other words, the company breaks even if they produce and sell 700 units. They neither make money nor lose money.
The shaded region to the right of the break-even point represents quantities for which the company makes a profit. The shaded region to the left represents quantities for which the company suffers a loss. The profit function is the revenue function minus the cost function, written as [latex]P\left(x\right)=R\left(x\right)-C\left(x\right)[/latex]. Clearly, knowing the quantity for which the cost equals the revenue is of great importance to businesses.
Example: Finding the Break-Even Point and the Profit Function Using Substitution
Given the cost function [latex]C\left(x\right)=0.85x+35{,}000[/latex] and the revenue function [latex]R\left(x\right)=1.55x[/latex], find the break-even point and the profit function.
Writing a System of Linear Equations Given a Situation
It is rare to be given equations that neatly model behaviors that you encounter in business, rather, you will probably be faced with a situation for which you know key information as in the example above. Below, we summarize three key factors that will help guide you in translating a situation into a system.
How To: Given a situation that represents a system of linear equations, write the system of equations and identify the solution.
- Identify the input and output of each linear model.
- Identify the slope and y-intercept of each linear model.
- Find the solution by setting the two linear functions equal to another and solving for x, or find the point of intersection on a graph.
Now let’s practice putting these key factors to work. In the next example, we determine how many different types of tickets are sold given information about the total revenue and amount of tickets sold to an event.
Example: Writing and Solving a System of Equations in Two Variables
The cost of a ticket to the circus is $25.00 for children and $50.00 for adults. On a certain day, attendance at the circus is 2,000 and the total gate revenue is $70,000. How many children and how many adults bought tickets?
Try It
Meal tickets at the circus cost $4.00 for children and $12.00 for adults. If 1,650 meal tickets were bought for a total of $14,200, how many children and how many adults bought meal tickets?
Sometimes, a system of equations can inform a decision. In our next example, we help answer the question, “Which truck rental company will give the best value?”
Example: Building a System of Linear Models to Choose a Truck Rental Company
Jamal is choosing between two truck-rental companies. The first, Keep on Trucking, Inc., charges an up-front fee of $20, then 59 cents a mile. The second, Move It Your Way, charges an up-front fee of $16, then 63 cents a mile.[1] When will Keep on Trucking, Inc. be the better choice for Jamal?
The applications for systems seems almost endless, but we will just show one more. In the next example, we determine the amount 80% methane solution to add to a 50% solution to give a final solution of 60%.
Example: Solve a Chemical Mixture Problem
A chemist has 70 mL of a 50% methane solution. How much of a 80% solution must she add so the final solution is 60% methane?
Try IT
Key Concepts
- A system of linear equations consists of two or more equations made up of two or more variables such that all equations in the system are considered simultaneously.
- The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently.
- Systems of equations are classified as independent with one solution, dependent with an infinite number of solutions, or inconsistent with no solution.
- One method of solving a system of linear equations in two variables is by graphing. In this method, we graph the equations on the same set of axes.
- Another method of solving a system of linear equations is by substitution. In this method, we solve for one variable in one equation and substitute the result into the second equation.
- A third method of solving a system of linear equations is by addition, in which we can eliminate a variable by adding opposite coefficients of corresponding variables.
- It is often necessary to multiply one or both equations by a constant to facilitate elimination of a variable when adding the two equations together.
- Either method of solving a system of equations results in a false statement for inconsistent systems because they are made up of parallel lines that never intersect.
- The solution to a system of dependent equations will always be true because both equations describe the same line.
- Systems of equations can be used to solve real-world problems that involve more than one variable, such as those relating to revenue, cost, and profit.
Glossary
addition method an algebraic technique used to solve systems of linear equations in which the equations are added in a way that eliminates one variable, allowing the resulting equation to be solved for the remaining variable; substitution is then used to solve for the first variable
break-even point the point at which a cost function intersects a revenue function; where profit is zero
consistent system a system for which there is a single solution to all equations in the system and it is an independent system, or if there are an infinite number of solutions and it is a dependent system
cost function the function used to calculate the costs of doing business; it usually has two parts, fixed costs and variable costs
dependent system a system of linear equations in which the two equations represent the same line; there are an infinite number of solutions to a dependent system
inconsistent system a system of linear equations with no common solution because they represent parallel lines, which have no point or line in common
independent system a system of linear equations with exactly one solution pair [latex]\left(x,y\right)[/latex]
profit function the profit function is written as [latex]P\left(x\right)=R\left(x\right)-C\left(x\right)[/latex], revenue minus cost
revenue function the function that is used to calculate revenue, simply written as [latex]R=xp[/latex], where [latex]x=[/latex] quantity and [latex]p=[/latex] price
substitution method an algebraic technique used to solve systems of linear equations in which one of the two equations is solved for one variable and then substituted into the second equation to solve for the second variable
system of linear equations a set of two or more equations in two or more variables that must be considered simultaneously.
- Rates retrieved Aug 2, 2010 from http://www.budgettruck.com and http://www.uhaul.com/ ↵