Because of the evolution of the number system, we can now perform complex calculations using several categories of real numbers. In this section we will explore sets of numbers, perform calculations with different kinds of numbers, and begin to learn about the use of numbers in algebraic expressions.

Classify a Real Number

The numbers we use for counting, or enumerating items, are the natural numbers: 1, 2, 3, 4, 5, and so on. We describe them in set notation as {1, 2, 3, …} where the ellipsis (…) indicates that the numbers continue to infinity. The natural numbers are, of course, also called the counting numbers. Any time we enumerate the members of a team, count the coins in a collection, or tally the trees in a grove, we are using the set of natural numbers. The set of whole numbers is the set of natural numbers plus zero: {0, 1, 2, 3,…}.

The set of integers adds the opposites of the natural numbers to the set of whole numbers: {…,-3, -2, -1, 0, 1, 2, 3,…}. It is useful to note that the set of integers is made up of three distinct subsets: negative integers, zero, and positive integers. In this sense, the positive integers are just the natural numbers. Another way to think about it is that the natural numbers are a subset of the integers.

The set of rational numbers is written as [latex]\left\{\frac{m}{n}|m\text{ and }{n}\text{ are integers and }{n}\ne{ 0 }\right\}[/latex]. Notice from the definition that rational numbers are fractions (or quotients) containing integers in both the numerator and the denominator, and the denominator is never 0. We can also see that every natural number, whole number, and integer is a rational number with a denominator of 1.

Because they are fractions, any rational number can also be expressed in decimal form. Any rational number can be represented as either:

1. a terminating decimal: [latex]\frac{15}{8}=1.875[/latex], or
2. a repeating decimal: [latex]\frac{4}{11}=0.36363636\dots =0.\overline{36}[/latex]

We use a line drawn over the repeating block of numbers instead of writing the group multiple times.

Irrational Numbers

At some point in the ancient past, someone discovered that not all numbers are rational numbers. A builder, for instance, may have found that the diagonal of a square with unit sides was not 2 or even [latex]\frac{3}{2}[/latex], but was something else. Or a garment maker might have observed that the ratio of the circumference to the diameter of a roll of cloth was a little bit more than 3, but still not a rational number. Such numbers are said to be irrational because they cannot be written as fractions. These numbers make up the set of irrational numbers. Irrational numbers cannot be expressed as a fraction of two integers. It is impossible to describe this set of numbers by a single rule except to say that a number is irrational if it is not rational. So we write this as shown.

{h | h is not a rational number}

Example: Differentiating Rational and Irrational Numbers

Determine whether each of the following numbers is rational or irrational. If it is rational, determine whether it is a terminating or repeating decimal.

1. [latex]\sqrt{25}[/latex]
2. [latex]\dfrac{33}{9}[/latex]
3. [latex]\sqrt{11}[/latex]
4. [latex]\dfrac{17}{34}[/latex]
5. [latex]0.3033033303333\dots[/latex]

Show Solution

1. [latex]\sqrt{25}:[/latex] This can be simplified as [latex]\sqrt{25}=5[/latex]. Therefore, [latex]\sqrt{25}[/latex] is rational.
2. [latex]\dfrac{33}{9}:[/latex] Because it is a fraction, [latex]\dfrac{33}{9}[/latex] is a rational number. Next, simplify and divide.
   [latex]\dfrac{33}{9}=\dfrac{{11}\cdot{3}}{{3}\cdot{3}}=\dfrac{11}{3}=3.\overline{6}[/latex]

   So, [latex]\dfrac{33}{9}[/latex] is rational and a repeating decimal.

3. [latex]\sqrt{11}:[/latex] This cannot be simplified any further. Therefore, [latex]\sqrt{11}[/latex] is an irrational number.
4. [latex]\dfrac{17}{34}:[/latex] Because it is a fraction, [latex]\dfrac{17}{34}[/latex] is a rational number. Simplify and divide.
   [latex]\dfrac{17}{34}=\dfrac{1\cdot{17}}{2\cdot{17}}=\dfrac{1}{2}=0.5[/latex]

   So, [latex]\dfrac{17}{34}[/latex] is rational and a terminating decimal.

5. 0.3033033303333… is not a terminating decimal. Also note that there is no repeating pattern because the group of 3s increases each time. Therefore it is neither a terminating nor a repeating decimal and, hence, not a rational number. It is an irrational number.

Try It

Real Numbers

Given any number n, we know that n is either rational or irrational. It cannot be both. The sets of rational and irrational numbers together make up the set of real numbers. As we saw with integers, the real numbers can be divided into three subsets: negative real numbers, zero, and positive real numbers. Each subset includes fractions, decimals, and irrational numbers according to their algebraic sign (+ or –). Zero is considered neither positive nor negative.

The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as 0, with negative numbers to the left of 0 and positive numbers to the right of 0. A fixed unit distance is then used to mark off each integer (or other basic value) on either side of 0. Any real number corresponds to a unique position on the number line. The converse is also true: each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line.

The real number line

Example: Classifying Real Numbers

Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?

1. [latex]-\dfrac{10}{3}[/latex]
2. [latex]\sqrt{5}[/latex]
3. [latex]-\sqrt{289}[/latex]
4. [latex]-6\pi[/latex]
5. [latex]0.616161\dots[/latex]
6. [latex] 0.13 [/latex]

Show Solution

1. [latex]-\dfrac{10}{3}[/latex] is negative and rational. It lies to the left of 0 on the number line.
2. [latex]\sqrt{5}[/latex] is positive and irrational. It lies to the right of 0.
3. [latex]-\sqrt{289}=-\sqrt{{17}^{2}}=-17[/latex] is negative and rational. It lies to the left of 0.
4. [latex]-6\pi [/latex] is negative and irrational. It lies to the left of 0.
5. [latex]0.616161\dots [/latex] is a repeating decimal so it is rational and positive. It lies to the right of 0.
6. [latex] 0.13 [/latex] is a finite decimal and may be written as 13/100.  So it is rational and positive.

Try It

Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?

1. [latex]\sqrt{73}[/latex]
2. [latex]-11.411411411\dots [/latex]
3. [latex]\dfrac{47}{19}[/latex]
4. [latex]-\dfrac{\sqrt{5}}{2}[/latex]
5. [latex]6.210735[/latex]

Show Solution

1. positive, irrational; right
2. negative, rational; left
3. positive, rational; right
4. negative, irrational; left
5. positive, rational; right

Sets of Numbers as Subsets

Beginning with the natural numbers, we have expanded each set to form a larger set, meaning that there is a subset relationship between the sets of numbers we have encountered so far. These relationships become more obvious when seen as a diagram.

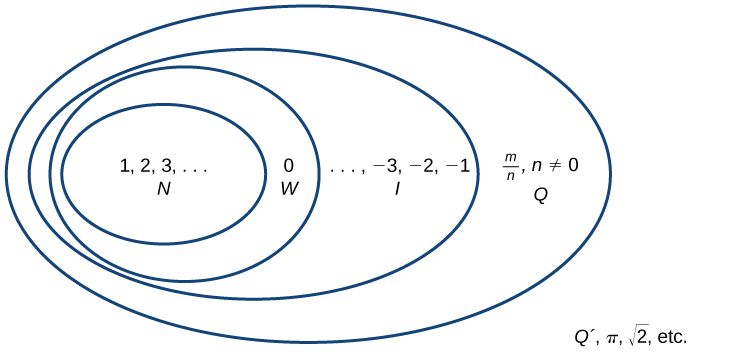
Sets of numbers.   N: the set of natural numbers   W: the set of whole numbers   I: the set of integers   Q: the set of rational numbers   Q´: the set of irrational numbers

A General Note: Sets of Numbers

The set of natural numbers includes the numbers used for counting: [latex]\{1,2,3,\dots\}[/latex].

The set of whole numbers is the set of natural numbers plus zero: [latex]\{0,1,2,3,\dots\}[/latex].

The set of integers adds the negative natural numbers to the set of whole numbers: [latex]\{\dots,-3,-2,-1,0,1,2,3,\dots\}[/latex].

The set of rational numbers includes fractions written as [latex]\{\frac{m}{n}|m\text{ and }n\text{ are integers and }n\ne 0\}[/latex].

The set of irrational numbers is the set of numbers that are not rational, are nonrepeating, and are nonterminating: [latex]\{h|h\text{ is not a rational number}\}[/latex].

Example: Differentiating the Sets of Numbers

Classify each number as being a natural number, whole number, integer, rational number, and/or irrational number.

• [latex]\sqrt{36}[/latex]
• [latex]\dfrac{8}{3}[/latex]
• [latex]\sqrt{73}[/latex]
• [latex]-6[/latex]
• [latex]3.2121121112\dots [/latex]

Show Solution

	natural number	whole number	integer	rational number	irrational number
[latex]\sqrt{36}=6[/latex]	yes	yes	yes	yes	no
[latex]\dfrac{8}{3}=2.\overline{6}[/latex]	no	no	no	yes	no
[latex]\sqrt{73}[/latex]	no	no	no	no	yes
[latex] –6 [/latex]	no	no	yes	yes	no
[latex]3.2121121112\dots[/latex]	no	no	no	no	yes

Try It

Classify each number as being a natural number (N), whole number (W), integer (I), rational number (Q), and/or irrational number (Q’).

1. [latex]-\dfrac{35}{7}[/latex]
2. [latex]0[/latex]
3. [latex]\sqrt{169}[/latex]
4. [latex]\sqrt{24}[/latex]
5. [latex]4.763763763\dots [/latex]

Show Solution

	natural number	whole number	integer	rational number	irrational number
[latex]-\dfrac{35}{7}[/latex]	no	no	yes	yes	no
[latex] 0 [/latex]	no	yes	yes	yes	no
[latex]\sqrt{169}[/latex]	yes	yes	yes	yes	no
[latex] \sqrt{24} [/latex]	no	no	no	no	yes
[latex]4.763763763\dots[/latex]	no	no	no	yes	no

Watch this video for an overview of the sets of numbers, and how to identify which set a number belongs to.

Properties of Real Numbers

When we multiply a number by itself, we square it or raise it to a power of 2. For example, [latex]{4}^{2}=4\cdot 4=16[/latex]. We can raise any number to any power. In general, the exponential notation [latex]{a}^{n}[/latex] means that the number or variable [latex]a[/latex] is used as a factor [latex]n[/latex] times.

In this notation, [latex]{a}^{n}[/latex] is read as the nth power of [latex]a[/latex], where [latex]a[/latex] is called the base and [latex]n[/latex] is called the exponent. A term in exponential notation may be part of a mathematical expression, which is a combination of numbers and operations. For example, [latex]24+6\cdot \frac{2}{3}-{4}^{2}[/latex] is a mathematical expression.

To evaluate a mathematical expression, we perform the various operations. However, we do not perform them in any random order. We use the order of operations. This is a sequence of rules for evaluating such expressions.

Recall that in mathematics we use parentheses ( ), brackets [ ], and braces { } to group numbers and expressions so that anything appearing within the symbols is treated as a unit. Additionally, fraction bars, radicals, and absolute value bars are treated as grouping symbols. When evaluating a mathematical expression, begin by simplifying expressions within grouping symbols.

The next step is to address any exponents or radicals. Afterward, perform multiplication and division from left to right and finally addition and subtraction from left to right.

Let’s take a look at the expression provided.

There are no grouping symbols, so we move on to exponents or radicals. The number 4 is raised to a power of 2, so simplify [latex]{4}^{2}[/latex] as 16.

Next, perform multiplication or division, left to right.

Lastly, perform addition or subtraction, left to right.

Therefore, [latex]24+6\cdot \dfrac{2}{3}-{4}^{2}=12[/latex].

For some complicated expressions, several passes through the order of operations will be needed. For instance, there may be a radical expression inside parentheses that must be simplified before the parentheses are evaluated. Following the order of operations ensures that anyone simplifying the same mathematical expression will get the same result.

Watch the following video for more examples of using the order of operations to simplify an expression.

Using Properties of Real Numbers

For some activities we perform, the order of certain operations does not matter, but the order of other operations does. For example, it does not make a difference if we put on the right shoe before the left or vice-versa. However, it does matter whether we put on shoes or socks first. The same thing is true for operations in mathematics.

Commutative Properties

The commutative property of addition states that numbers may be added in any order without affecting the sum.

We can better see this relationship when using real numbers.

Similarly, the commutative property of multiplication states that numbers may be multiplied in any order without affecting the product.

Again, consider an example with real numbers.

It is important to note that neither subtraction nor division is commutative. For example, [latex]17 - 5[/latex] is not the same as [latex]5 - 17[/latex]. Similarly, [latex]20\div 5\ne 5\div 20[/latex].

Associative Properties

The associative property of multiplication tells us that it does not matter how we group numbers when multiplying. We can move the grouping symbols to make the calculation easier, and the product remains the same.

Consider this example.

The associative property of addition tells us that numbers may be grouped differently without affecting the sum.

This property can be especially helpful when dealing with negative integers. Consider this example.

Are subtraction and division associative? Review these examples.

As we can see, neither subtraction nor division is associative.

Distributive Property

The distributive property states that the product of a factor times a sum is the sum of the factor times each term in the sum.

This property combines both addition and multiplication (and is the only property to do so). Let us consider an example.

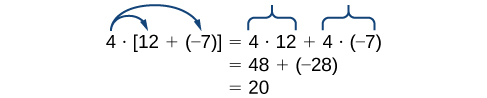
Note that 4 is outside the grouping symbols, so we distribute the 4 by multiplying it by 12, multiplying it by –7, and adding the products.

To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.

Multiplication does not distribute over subtraction, and division distributes over neither addition nor subtraction.

A special case of the distributive property occurs when a sum of terms is subtracted.

For example, consider the difference [latex]12-\left(5+3\right)[/latex]. We can rewrite the difference of the two terms 12 and [latex]\left(5+3\right)[/latex] by turning the subtraction expression into addition of the opposite. So instead of subtracting [latex]\left(5+3\right)[/latex], we add the opposite.

Now, distribute [latex]-1[/latex] and simplify the result.

This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.

Identity Properties

The identity property of addition states that there is a unique number, called the additive identity (0) that, when added to a number, results in the original number.

The identity property of multiplication states that there is a unique number, called the multiplicative identity (1) that, when multiplied by a number, results in the original number.

For example, we have [latex]\left(-6\right)+0=-6[/latex] and [latex]23\cdot 1=23[/latex]. There are no exceptions for these properties; they work for every real number, including 0 and 1.

Inverse Properties

The inverse property of addition states that, for every real number a, there is a unique number, called the additive inverse (or opposite), denoted−a, that, when added to the original number, results in the additive identity, 0.

For example, if [latex]a=-8[/latex], the additive inverse is 8, since [latex]\left(-8\right)+8=0[/latex].

The inverse property of multiplication holds for all real numbers except 0 because the reciprocal of 0 is not defined. The property states that, for every real number a, there is a unique number, called the multiplicative inverse (or reciprocal), denoted [latex]\frac{1}{a}[/latex], that, when multiplied by the original number, results in the multiplicative identity, 1.

For example, if [latex]a=-\frac{2}{3}[/latex], the reciprocal, denoted [latex]\frac{1}{a}[/latex], is [latex]-\frac{3}{2}[/latex] because

Evaluate and Simplify Algebraic Expressions

So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as [latex]x+5,\frac{4}{3}\pi {r}^{3}[/latex], or [latex]\sqrt{2{m}^{3}{n}^{2}}[/latex]. In the expression [latex]x+5, 5[/latex] is called a constant because it does not vary and x is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.

We have already seen some real number examples of exponential notation, a shorthand method of writing products of the same factor. When variables are used, the constants and variables are treated the same way.

In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.

Any variable in an algebraic expression may take on or be assigned different values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before.

In the following video we present more examples of how to evaluate an expression for a given value.

Formulas

An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation [latex]2x+1=7[/latex] has the unique solution [latex]x=3[/latex] because when we substitute 3 for [latex]x[/latex] in the equation, we obtain the true statement [latex]2\left(3\right)+1=7[/latex].

A formula is an equation expressing a relationship between constant and variable quantities. Very often the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area [latex]A[/latex] of a circle in terms of the radius [latex]r[/latex] of the circle: [latex]A=\pi {r}^{2}[/latex]. For any value of [latex]r[/latex], the area [latex]A[/latex] can be found by evaluating the expression [latex]\pi {r}^{2}[/latex].

Example: Using a Formula

A right circular cylinder with radius [latex]r[/latex] and height [latex]h[/latex] has the surface area [latex]S[/latex] (in square units) given by the formula [latex]S=2\pi r\left(r+h\right)[/latex]. Find the surface area of a cylinder with radius 6 in. and height 9 in. Leave the answer in terms of [latex]\pi[/latex].

Right circular cylinder

Show Solution

Evaluate the expression [latex]2\pi r\left(r+h\right)[/latex] for [latex]r=6[/latex] and [latex]h=9[/latex].

[latex]\begin{align}S&=2\pi r\left(r+h\right) \\ & =2\pi\left(6\right)[\left(6\right)+\left(9\right)] \\ & =2\pi\left(6\right)\left(15\right) \\ & =180\pi\end{align}[/latex]

The surface area is [latex]180\pi [/latex] square inches.

Try It

Figure 4

A photograph with length L and width W is placed in a mat of width 8 centimeters (cm). The area of the mat (in square centimeters, or cm²) is found to be [latex]A=\left(L+16\right)\left(W+16\right)-L\cdot W[/latex]. Find the area of a mat for a photograph with length 32 cm and width 24 cm.

Show Solution

1,152 cm²

Simplify Algebraic Expressions

Sometimes we can simplify an algebraic expression to make it easier to evaluate or to use in some other way. To do so, we use the properties of real numbers. We can use the same properties in formulas because they contain algebraic expressions.

Key Concepts

• Rational numbers may be written as fractions or terminating or repeating decimals.
• Determine whether a number is rational or irrational by writing it as a decimal.
• The rational numbers and irrational numbers make up the set of real numbers. A number can be classified as natural, whole, integer, rational, or irrational.
• The order of operations is used to evaluate expressions.
• The real numbers under the operations of addition and multiplication obey basic rules, known as the properties of real numbers. These are the commutative properties, the associative properties, the distributive property, the identity properties, and the inverse properties.
• Algebraic expressions are composed of constants and variables that are combined using addition, subtraction, multiplication, and division. They take on a numerical value when evaluated by replacing variables with constants.
• Formulas are equations in which one quantity is represented in terms of other quantities. They may be simplified or evaluated as any mathematical expression.

Glossary

algebraic expression constants and variables combined using addition, subtraction, multiplication, and division

associative property of addition the sum of three numbers may be grouped differently without affecting the result; in symbols, [latex]a+\left(b+c\right)=\left(a+b\right)+c[/latex]

associative property of multiplication the product of three numbers may be grouped differently without affecting the result; in symbols, [latex]a\cdot \left(b\cdot c\right)=\left(a\cdot b\right)\cdot c[/latex]

base in exponential notation, the expression that is being multiplied

commutative property of addition two numbers may be added in either order without affecting the result; in symbols, [latex]a+b=b+a[/latex]

commutative property of multiplication two numbers may be multiplied in any order without affecting the result; in symbols, [latex]a\cdot b=b\cdot a[/latex]

constant a quantity that does not change value

distributive property the product of a factor times a sum is the sum of the factor times each term in the sum; in symbols, [latex]a\cdot \left(b+c\right)=a\cdot b+a\cdot c[/latex]

equation a mathematical statement indicating that two expressions are equal

exponent in exponential notation, the raised number or variable that indicates how many times the base is being multiplied

exponential notation a shorthand method of writing products of the same factor

formula an equation expressing a relationship between constant and variable quantities

identity property of addition there is a unique number, called the additive identity, 0, which, when added to a number, results in the original number; in symbols, [latex]a+0=a[/latex]

identity property of multiplication there is a unique number, called the multiplicative identity, 1, which, when multiplied by a number, results in the original number; in symbols, [latex]a\cdot 1=a[/latex]

integers the set consisting of the natural numbers, their opposites, and 0: [latex]\{\dots ,-3,-2,-1,0,1,2,3,\dots \}[/latex]

inverse property of addition for every real number [latex]a[/latex], there is a unique number, called the additive inverse (or opposite), denoted [latex]-a[/latex], which, when added to the original number, results in the additive identity, 0; in symbols, [latex]a+\left(-a\right)=0[/latex]

inverse property of multiplication for every non-zero real number [latex]a[/latex], there is a unique number, called the multiplicative inverse (or reciprocal), denoted [latex]\dfrac{1}{a}[/latex], which, when multiplied by the original number, results in the multiplicative identity, 1; in symbols, [latex]a\cdot \dfrac{1}{a}=1[/latex]

irrational numbers the set of all numbers that are not rational; they cannot be written as either a terminating or repeating decimal; they cannot be expressed as a fraction of two integers

natural numbers the set of counting numbers: [latex]\{1,2,3,\dots \}[/latex]

order of operations a set of rules governing how mathematical expressions are to be evaluated, assigning priorities to operations

rational numbers the set of all numbers of the form [latex]\dfrac{m}{n}[/latex], where [latex]m[/latex] and [latex]n[/latex] are integers and [latex]n\ne 0[/latex]. Any rational number may be written as a fraction or a terminating or repeating decimal.

real number line a horizontal line used to represent the real numbers. An arbitrary fixed point is chosen to represent 0; positive numbers lie to the right of 0 and negative numbers to the left.

real numbers the sets of rational numbers and irrational numbers taken together

variable a quantity that may change value

whole numbers the set consisting of 0 plus the natural numbers: [latex]\{0,1,2,3,\dots \}[/latex]