Learning Objectives
- Find the product of monomials
- Find the product of polynomials and monomials
- Find the product of two binomials
Find the product of monomials
Multiplying polynomials involves applying the rules of exponents and the distributive property to simplify the product. Polynomial multiplication can be useful in modeling real world situations. Understanding polynomial products is an important step in learning to solve algebraic equations involving polynomials. There are many, varied uses for polynomials including the generation of 3D graphics for entertainment and industry, as in the image below.
Surfaces made from polynomials with AutoCAD
In the exponents section, we practiced multiplying monomials together, like we did with this expression: [latex]24{x}^{8}2{x}^{5}[/latex]. The only thing different between that section and this one is that we called it simplifying, and now we are calling it polynomial multiplication. Remember that simplifying a mathematical expression means performing as many operations as we can until there are no more to perform, including multiplication. In this section we will show examples of how to multiply more than just monomials. We will multiply monomials with binomials and trinomials. We will also learn some techniques for multiplying two binomials together.
Example
Multiply. [latex]-9x^{3}\cdot 3x^{2}[/latex]
That’s it! When multiplying monomials, multiply the coefficients together, and then multiply the variables together. Remember, if two variables have the same base, follow the rules of exponents, like this:
[latex]\displaystyle 5{{a}^{4}}\cdot 7{{a}^{6}}=35{{a}^{10}}[/latex]
The following video provides more examples of multiplying monomials with different exponents.
Find the product of polynomials and monomials
The distributive property can be used to multiply a monomial and a binomial. Just remember that the monomial must be multiplied by each term in the binomial. In the next example, you will see how to multiply a second degree monomial with a binomial. Note the use of exponent rules.
Example
Simplify. [latex]5x^2\left(4x^{2}+3x\right)[/latex]
Now let’s add another layer by multiplying a monomial by a trinomial. Consider the expression [latex]2x\left(2x^{2}+5x+10\right)[/latex].
This expression can be modeled with a sketch like the one below.

The only difference between this example and the previous one is there is one more term to distribute the monomial to.
[latex]\begin{array}{c}2x\left(2x^{2}+5x+10\right)=2x\left(2x^{2}\right)+2x\left(5x\right)=2x\left(10\right)\\=4x^{3}+10x^{2}+20x\end{array}[/latex]
You will always need to pay attention to negative signs when you are multiplying. Watch what happens to the sign on the terms in the trinomial when it is multiplied by a negative monomial in the next example.
Example
Simplify. [latex]-7x\left(2x^{2}-5x+1\right)[/latex]
The following video provides more examples of multiplying a monomial and a polynomial.
Find the product of two binomials
Now let’s explore multiplying two binomials. For those of you that use pictures to learn, you can draw an area model to help make sense of the process. You’ll use each binomial as one of the dimensions of a rectangle, and their product as the area.
The model below shows [latex]\left(x+4\right)\left(x+2\right)[/latex]:
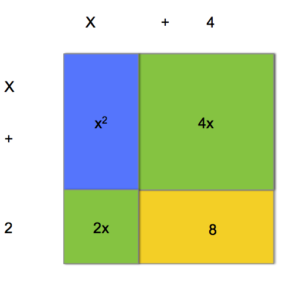
Visual representation of multiplying two binomials.
Each binomial is expanded into variable terms and constants, [latex]x+4[/latex], along the top of the model and [latex]x+2[/latex] along the left side. The product of each pair of terms is a colored rectangle. The total area is the sum of all of these small rectangles, [latex]x^{2}+2x+4x+8[/latex], If you combine all the like terms, you can write the product, or area, as [latex]x^{2}+6x+8[/latex].
You can use the distributive property to determine the product of two binomials.
Example
Simplify. [latex]\left(x+4\right)\left(x+2\right)[/latex]
Look back at the model above to see where each piece of [latex]x^{2}+2x+4x+8[/latex] comes from. Can you see where you multiply [latex]x[/latex] by [latex]x + 2[/latex], and where you get [latex]x^{2}[/latex] from [latex]x\left(x\right)[/latex]?
Another way to look at multiplying binomials is to see that each term in one binomial is multiplied by each term in the other binomial. Look at the example above: the [latex]x[/latex] in [latex]x+4[/latex] gets multiplied by both the [latex]x[/latex] and the 2 from [latex]x+2[/latex], and the 4 gets multiplied by both the [latex]x[/latex] and the 2.
The following video provides an example of multiplying two binomials using an area model as well as repeated distribution.
In the next section we will explore other methods for multiplying two binomials, and become aware of the different forms that binomials can have.
Candela Citations
- Ex: Multiplying Monomials. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/30x8hY32B0o. License: CC BY: Attribution
- Ex: Multiplying Using the Distributive Property. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/bwTmApTV_8o. License: CC BY: Attribution
- Multiply Binomials Using An Area Model and Using Repeated Distribution. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/u4Hgl0BrUlo. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution