Composite and Inverse Functions

Learning Objectives

  • Composite and Inverse Functions
    • Define a composite function
    • Define an inverse function
    • Use compositions of functions to verify inverses algebraically
    • Identify an inverse algebraically
Photo of the aftermath of the earthquake in Japan with a focus on the Japanese flag.

Figure 1. Devastation of March 11, 2011 earthquake in Honshu, Japan. (credit: Daniel Pierce)

In 2010, a major earthquake struck Haiti, destroying or damaging over 285,000 homes.[1] One year later, another, stronger earthquake devastated Honshu, Japan, destroying or damaging over 332,000 buildings,[2] like those shown in the picture above. Even though both caused substantial damage, the earthquake in 2011 was 100 times stronger than the earthquake in Haiti. How do we know? The magnitudes of earthquakes are measured on a scale known as the Richter Scale. The Haitian earthquake registered a 7.0 on the Richter Scale[3] whereas the Japanese earthquake registered a 9.0.[4]

The Richter Scale is a base-ten logarithmic scale. In other words, an earthquake of magnitude 8 is not twice as great as an earthquake of magnitude 4. It is [latex]{10}^{8 - 4}={10}^{4}=10,000[/latex] times as great! In this lesson, we will investigate the nature of the Richter Scale and the base-ten function upon which it depends.

Our first topic will be about inverse functions, logarithmic functions are the inverse of an exponential functions, and sometimes understanding this helps us make sense of what a logarithm is.

Composite and Inverse Functions

Suppose we want to calculate how much it costs to heat a house on a particular day of the year. The cost to heat a house will depend on the average daily temperature, and in turn, the average daily temperature depends on the particular day of the year. Notice how we have just defined two relationships: The cost depends on the temperature, and the temperature depends on the day.

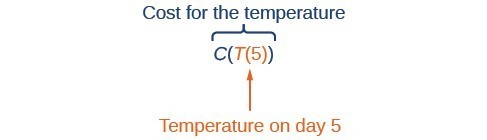
Explanation of C(T(5)), which is the cost for the temperature and T(5) is the temperature on day 5.

Figure 1

Using descriptive variables, we can notate these two functions. The function [latex]C\left(T\right)[/latex] gives the cost [latex]C[/latex] of heating a house for a given average daily temperature in [latex]T[/latex] degrees Celsius. The function [latex]T\left(d\right)[/latex] gives the average daily temperature on day [latex]d[/latex] of the year. For any given day, [latex]\text{Cost}=C\left(T\left(d\right)\right)[/latex] means that the cost depends on the temperature, which in turns depends on the day of the year. Thus, we can evaluate the cost function at the temperature [latex]T\left(d\right)[/latex]. For example, we could evaluate [latex]T\left(5\right)[/latex] to determine the average daily temperature on the 5th day of the year. Then, we could evaluate the cost function at that temperature. We would write [latex]C\left(T\left(5\right)\right)[/latex]. By combining these two relationships into one function, we have performed function composition.

We read the left-hand side as [latex]``f[/latex] composed with [latex]g[/latex] at [latex]x,''[/latex] and the right-hand side as [latex]``f[/latex] of [latex]g[/latex] of [latex]x.''[/latex] The two sides of the equation have the same mathematical meaning and are equal. The open circle symbol [latex]\circ [/latex] is called the composition operator.

It is also important to understand the order of operations in evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first, and then working to the outside.

 

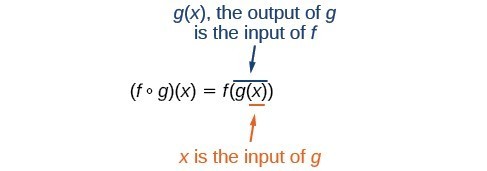
Explanation of the composite function. g(x), the output of g is the input of f. X is the input of g.

Example

Using the functions provided, find [latex]f\left(g\left(x\right)\right)[/latex] and [latex]g\left(f\left(x\right)\right)[/latex].

[latex]f\left(x\right)=2x+1[/latex]

[latex]g\left(x\right)=3-x[/latex]

In the following video you will see another example of how to find the composition of two functions.

Inverse Functions

An inverse function is a function for which the input of the original function becomes the output of the inverse function. This naturally leads to the output of the original function becoming the input of the inverse function. The reason we want to introduce inverse functions is because exponential and logarithmic functions are inverses of each other, and understanding this quality helps to make understanding logarithmic functions easier. And the reason we introduced composite functions is because you can verify, algebraically, whether two functions are inverses of each other by using a composition.

Given a function [latex]f\left(x\right)[/latex], we represent its inverse as [latex]{f}^{-1}\left(x\right)[/latex], read as [latex]``f[/latex] inverse of [latex]x.''[/latex] The raised [latex]-1[/latex] is part of the notation. It is not an exponent; it does not imply a power of [latex]-1[/latex] . In other words, [latex]{f}^{-1}\left(x\right)[/latex] does not mean [latex]\frac{1}{f\left(x\right)}[/latex] because [latex]\frac{1}{f\left(x\right)}[/latex] is the reciprocal of [latex]f[/latex] and not the inverse.

Just as zero does not have a reciprocal, some functions do not have inverses.

Inverse Function

For any one-to-one function [latex]f\left(x\right)=y[/latex], a function [latex]{f}^{-1}\left(x\right)[/latex] is an inverse function of [latex]f[/latex] if [latex]{f}^{-1}\left(y\right)=x[/latex].

The notation [latex]{f}^{-1}[/latex] is read [latex]\text{``}f[/latex] inverse.” Like any other function, we can use any variable name as the input for [latex]{f}^{-1}[/latex], so we will often write [latex]{f}^{-1}\left(x\right)[/latex], which we read as [latex]``f[/latex] inverse of [latex]x.''[/latex]
Keep in mind that

[latex]{f}^{-1}\left(x\right)\ne \frac{1}{f\left(x\right)}[/latex]

and not all functions have inverses.

In our first example we will identify an inverse function from ordered pairs.

Example

If for a particular one-to-one function [latex]f\left(2\right)=4[/latex] and [latex]f\left(5\right)=12[/latex], what are the corresponding input and output values for the inverse function?

Analysis of the Solution

Notice that if we show the coordinate pairs in a table form, the input and output are clearly reversed.

[latex]\left(x,f\left(x\right)\right)[/latex] [latex]\left(x,g\left(x\right)\right)[/latex]
[latex]\left(2,4\right)[/latex] [latex]\left(4,2\right)[/latex]
[latex]\left(5,12\right)[/latex] [latex]\left(12,5\right)[/latex]

In the following video we show an example of finding corresponding input and output values given two ordered pairs from functions that are inverses.

How To: Given two functions [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)[/latex], test whether the functions are inverses of each other.

  1. Substitute [latex]g(x)[/latex] into [latex]f(x)[/latex]. The result must be [latex]x[/latex]. [latex]f\left(g(x)\right)=x[/latex]
  2. Substitute [latex]f(x)[/latex] into [latex]g(x)[/latex]. The result must be [latex]x[/latex]. [latex]g\left(f(x)\right)=x[/latex]

If [latex]f(x)[/latex] and  [latex]g(x)[/latex] are inverses, then  [latex]f(x)=g^{-1}(x)[/latex] and [latex]g(x)=f^{-1}(x)[/latex]

In our next example we will test inverse relationships algebraically.

Example

If [latex]f\left(x\right)=x^2-3[/latex], for [latex]x\ge0[/latex] and [latex]g\left(x\right)=\sqrt{x+3}[/latex], is [latex]g[/latex] the inverse of [latex]f[/latex]?  [latex]g={f}^{-1}?[/latex]

In the following video we use algebra to determine if two functions are inverses.

We will show one more example of how to verify whether you have an inverse algebraically.

Example

If [latex]f\left(x\right)=\frac{1}{x+2}[/latex] and [latex]g\left(x\right)=\frac{1}{x}-2[/latex], is [latex]g[/latex] the inverse of [latex]f[/latex]?  [latex]g={f}^{-1}?[/latex]

We will show one more example of how to use algebra to determine whether two functions are inverses of each other.

  1. http://earthquake.usgs.gov/earthquakes/eqinthenews/2010/us2010rja6/#summary. Accessed 3/4/2013. ↵
  2. http://earthquake.usgs.gov/earthquakes/eqinthenews/2011/usc0001xgp/#summary. Accessed 3/4/2013. ↵
  3. http://earthquake.usgs.gov/earthquakes/eqinthenews/2010/us2010rja6/. Accessed 3/4/2013. ↵
  4. http://earthquake.usgs.gov/earthquakes/eqinthenews/2011/usc0001xgp/#details. Accessed 3/4/2013. ↵