Skills Review for A Preview of Calculus

Learning Outcomes

  • Use the slope formula to find the slope of a line between two points

A Preview of Calculus discusses some of the various applications of calculus including how calculus is used to calculate the instantaneous rate of change or slope of a tangent line. To help build the idea of calculating the instantaneous rate of change, how to calculate the slope of a line using two points is reviewed here.

Calculate the Slope of a Line

The slope of a line refers to the ratio of the vertical change in y over the horizontal change in x between any two points on a line. It indicates the direction in which a line slants as well as its steepness. Slope is sometimes described as rise over run.

[latex]m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]

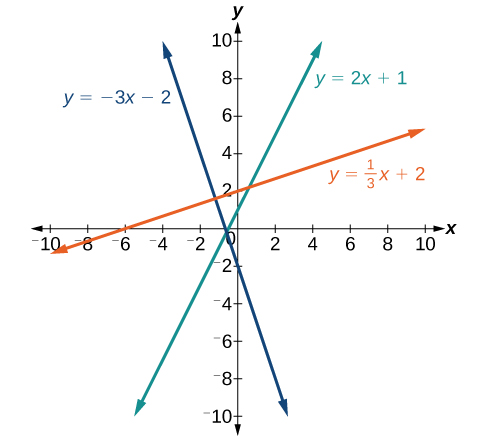
If the slope is positive, the line slants upward to the right. If the slope is negative, the line slants downward to the right. As the slope increases, the line becomes steeper. Some examples are shown below. The lines indicate the following slopes: [latex]m=-3[/latex], [latex]m=2[/latex], and [latex]m=\frac{1}{3}[/latex].

Coordinate plane with the x and y axes ranging from negative 10 to 10. Three linear functions are plotted: y = negative 3 times x minus 2; y = 2 times x plus 1; and y = x over 3 plus 2.

A General Note: The Slope of a Line

The slope of a line, m, represents the change in y over the change in x. Given two points, [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the following formula determines the slope of a line containing these points:

[latex]m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]

Example: Finding the Slope of a Line Given Two Points

Find the slope of a line that passes through the points [latex]\left(2,-1\right)[/latex] and [latex]\left(-5,3\right)[/latex].

Try It

Find the slope of the line that passes through the points [latex]\left(-2,6\right)[/latex] and [latex]\left(1,4\right)[/latex].